1 前言
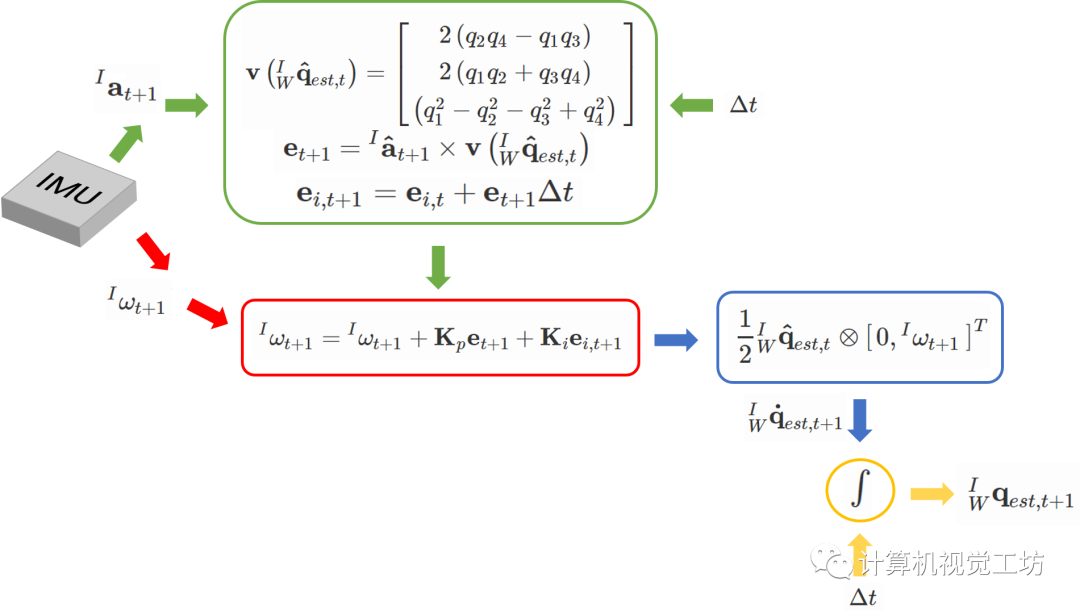
Mahony算法常見的姿態(tài)融合算法,根據(jù)加速度計、陀螺儀、以及磁力計,融合計算機體四元數(shù),計算速度快、精度較高。本文介紹六軸融合,即根據(jù)加速度計和陀螺儀數(shù)據(jù),計算姿態(tài)。
我們需要計算的是機體的姿態(tài)。計算角度可以通過角速度積分,也可以通過加速度正交分解,但這兩種方法都存在缺陷。角速度的誤差會隨著積分不斷增大,而加速度存在高頻噪聲,因此希望融合兩種數(shù)據(jù)。
2 算法
2.1 重力對齊誤差
首先要指出的是,Mahony算法假設(shè)加速度計測量的加速度完全由重力提供,即物體本體運動產(chǎn)生的加速度可忽略不計。在這一假設(shè)下,我們假設(shè)當前時刻機體的姿態(tài)為,則將重力向量的表示轉(zhuǎn)到機體坐標系下,應(yīng)該為:,這里表示四元數(shù)對應(yīng)的旋轉(zhuǎn)矩陣:
進一步地,帶入,得到
我們計加速度計測量得到的加速度,如果此時沒有誤差,應(yīng)該有,但實際兩個向量并不重合,存在一定的誤差 。
為表示出,可以利用向量的叉乘:。因為叉乘的定義為:,當歸一化為單位向量時,反應(yīng)的就是角度。這里更準確的寫為,下一時刻{t+1}時的誤差為:
其中 為根據(jù)當前{t}時刻估計的角度四元數(shù)。再記這個誤差的積分量為:
誤差的積分量也參與了后續(xù)計算。
2.2 角速度融合
此時已經(jīng)計算出加速度計觀測出的誤差了,記陀螺儀提供的角速度為,則把陀螺儀角速度的誤差加上上述的誤差,采用控制中常用的比例-積分控制器思想,
得到糾正的角速度。
討論:為什么用叉乘?
陀螺儀由于本身精度問題,測量的角速度存在誤差,在積分過程中這個誤差會一直累加,我們要做的就是去消除或是補償這個誤差,因為加速度計長期的測量值是準確的,所以可以用加速度計來進行修正。如何找到一個另一個角速度量綱的值來修正陀螺儀的角速度值呢?這里明明只有陀螺儀可以測量角速度!這時候前面提到的向量叉積得到的誤差向量就幫上大忙了,這個誤差向量不就是反映出了角度變化量嗎。算法巧妙的將加速度相關(guān)量轉(zhuǎn)化為角度相關(guān)量,因而可以用這個角度值乘一個系數(shù)來修正陀螺儀的角速度,因為在偏差角度很小的情況下,我們可以將陀螺儀角速度誤差和加速度計求得的角度差看做正比的關(guān)系,也就說明陀螺儀積分誤差和向量叉積存在正比關(guān)系。[2]
歡迎關(guān)注微信公眾號「3D視覺工坊」,加群/文章投稿/課程主講,請加微信:QYong2014,添加時請備注:加群/投稿/主講申請
方向主要包括:3D視覺領(lǐng)域各細分方向,比如相機標定|三維點云|三維重建|視覺/激光SLAM|感知|控制規(guī)劃|模型部署|3D目標檢測|TOF|多傳感器融合|AR|VR|編程基礎(chǔ)等。
2.3 計算下一時刻四元數(shù)
此時我們已經(jīng)獲取了下一時刻糾正后的角速度 ,這時候需要計算下一時刻的角度。
我們知道[3]四元數(shù)對時間的導(dǎo)數(shù)與角速度的關(guān)系為 ,即有
此時,再采用歐拉積分[4],即可得到下一時刻姿態(tài)與當前時刻姿態(tài)的關(guān)系:
從而完成了下一時刻姿態(tài)的計算。
3 核心代碼解析
我們以Matlab代碼為例,結(jié)合上述內(nèi)容進行介紹:
functionobj=UpdateIMU(obj,Gyroscope,Accelerometer)
q=obj.Quaternion;%當前時刻的四元數(shù)
%歸一化加速度計測量數(shù)據(jù)
if(norm(Accelerometer)==0),return;end%handleNaN
Accelerometer=Accelerometer/norm(Accelerometer);%normalisemagnitude
%計算重力在當前四元數(shù)位姿下的分量,即上述公式(2)
v=[2*(q(2)*q(4)-q(1)*q(3))
2*(q(1)*q(2)+q(3)*q(4))
q(1)^2-q(2)^2-q(3)^2+q(4)^2];
%計算重力分量與加速度計的測量誤差,上述公式(3)
e=cross(Accelerometer,v);
if(obj.Ki>0)
obj.eInt=obj.eInt+e*obj.SamplePeriod;%計算誤差的積分,公式(4)
else
obj.eInt=[000];
end
%角速度融合,公式(5)
Gyroscope=Gyroscope+obj.Kp*e+obj.Ki*obj.eInt;
%公式(6)
qDot=0.5*quaternProd(q,[0Gyroscope(1)Gyroscope(2)Gyroscope(3)]);
%歐拉積分計算下一時刻四元數(shù),公式(7)
q=q+qDot*obj.SamplePeriod;
obj.Quaternion=q/norm(q);%結(jié)果歸一化
end
4 完整代碼獲取
官方C++/Matlab/C#代碼:https://x-io.co.uk/open-source-imu-and-ahrs-algorithms/
官方python代碼:https://github.com/xioTechnologies/Fusion/tree/main/Python
第三方python姿態(tài)解算庫:https://ahrs.readthedocs.io/en/latest/filters/mahony.html
-
算法
+關(guān)注
關(guān)注
23文章
4701瀏覽量
94843 -
加速度計
+關(guān)注
關(guān)注
6文章
716瀏覽量
46639 -
濾波算法
+關(guān)注
關(guān)注
2文章
89瀏覽量
13913
發(fā)布評論請先 登錄
理解Mahony濾波算法的實現(xiàn)過程
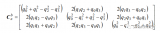
姿態(tài)解算(mahony算法):歐拉角的驗證
無人機設(shè)計中姿態(tài)檢測算法、姿態(tài)控制算法有什么區(qū)別 ?
請問IMU和AHRS算法用stm32如何實現(xiàn)?
四軸基礎(chǔ)算法學(xué)習(xí)——IMU輸入濾波算法
姿態(tài)融合算法是什么
PID算法的代碼實現(xiàn)
姿態(tài)解算算法模塊理解
LINS算法的框架與代碼分析
Mahony算法常見的姿態(tài)融合算法

經(jīng)典的濾波算法:Madgwick濾波算法





 IMU姿態(tài)濾波算法——Mahony算法:原理與代碼
IMU姿態(tài)濾波算法——Mahony算法:原理與代碼










評論