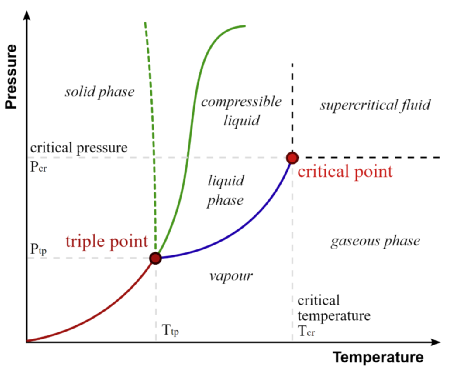
相變

物理系統(tǒng)中發(fā)生的相變最直觀，水結(jié)成冰或沸騰成蒸汽。在一定的溫度或壓力下，系統(tǒng)發(fā)生行為的突然變化，從一種相轉(zhuǎn)變?yōu)榱硪环N相。轉(zhuǎn)變出現(xiàn)了之前相中沒有的新特性，例如冰的晶體結(jié)構(gòu)或蒸汽的氣態(tài)特性。

相變應(yīng)該是自然界的基本特征之一，例如科學(xué)家發(fā)現(xiàn)即使在絕對零度，量子漲落也可引發(fā)量子相變。相變普遍存在于從原子到星系等各種系統(tǒng)中，而且不限于物理系統(tǒng)，化學(xué)、社會、經(jīng)濟、生物進化、腦科學(xué)和信息系統(tǒng)等等領(lǐng)域也普遍存在。股市的突然崩盤、抗議活動的爆發(fā)就可以被看作是社會系統(tǒng)中的相變。

那“相”是什么呢？以物理系統(tǒng)為例，仔細體會，"相"其實是空間密度函數(shù)，而且是隨時間變化的空間密度函數(shù)，ρ ( Space , T )。空間密度函數(shù)的突變，就是相變。如果我們把物體里面的原子密度函數(shù)寫作 ρ，然后用一組基函數(shù) ?i 把 ρ 展開 ρ=Σηi?i，即把密度函數(shù)展開成了空間里的一個矢量 η。也就是基函數(shù) ?i 張成的空間中，ρ 可以表示成向量η 。這樣“相”也就可以表征成 η的函數(shù)：“相”= F (η)。這樣相變就被刻畫成了數(shù)學(xué)形式。筆者一直試圖抑制使用數(shù)學(xué)公式的沖動，但這里表述起來很方便，且可以為讀者學(xué)習(xí)朗道相變理論開個頭，看看朗道如何將復(fù)雜物理現(xiàn)象建模成數(shù)學(xué)問題。

相變也可以被視為一個臨界點（Critical Point），系統(tǒng)的行為在此臨界點處會發(fā)生突變。在這個臨界點上，溫度或壓力的微小變化可以導(dǎo)致系統(tǒng)性質(zhì)的巨大改變。這是因為系統(tǒng)處于兩個相之間的邊界上，小的擾動可以推動它落入其中一個相或另一個相。相變可能導(dǎo)致出乎意料的涌現(xiàn)（emergent） 現(xiàn)象。理解相變可以幫助我們更好地理解和預(yù)測復(fù)雜系統(tǒng)中的這些突然變化，以便更好的理解和掌握涌現(xiàn)現(xiàn)象。

復(fù)雜系統(tǒng)涌現(xiàn)

1977 年諾貝爾物理學(xué)獎得主菲利普 · 安德森在 Science 上發(fā)表了他的傳世之作《More Is Different》，書中安德森認為復(fù)雜系統(tǒng)就是不能簡單地歸納為其各部分之和的系統(tǒng)。因為這些系統(tǒng)的行為不能通過研究其個體組成部分來預(yù)測。他運用物理學(xué)、生物學(xué)和社會學(xué)等領(lǐng)域的例子說明了這一點，強調(diào)了復(fù)雜系統(tǒng)的涌現(xiàn)現(xiàn)象不能簡單地通過了解其個體部分的屬性來解釋。

復(fù)雜系統(tǒng)表現(xiàn)出的涌現(xiàn)現(xiàn)象，并不在單個組成部分中存在。涌現(xiàn)是由系統(tǒng)組件之間的相互作用和關(guān)系產(chǎn)生的新屬性，僅僅通過研究單個組件是不能解釋的。牛頓力學(xué)導(dǎo)致的精確極致的還原主義不是有效地理解復(fù)雜系統(tǒng)的方法。在某些情況下，研究系統(tǒng)的組成部分可能反而會導(dǎo)致有關(guān)整個系統(tǒng)的信息喪失。這是因為涌現(xiàn)經(jīng)常源于系統(tǒng)組件之間的相互作用，而單獨研究組件可能會掩蓋這些相互作用。

鐵磁材料的磁性質(zhì)，低溫下某些材料的超導(dǎo)性，都是來自材料中原子與電子的集體行為，生物系統(tǒng)蟻群或鳥群的行為，語言、文化和政治制度等社會現(xiàn)象，都不能僅僅通過理解個體的特性來解釋，而是需要了解他們的集體行為和互動。

對稱性破缺

相變往往伴隨著新對稱性或?qū)ΨQ性破缺的出現(xiàn)，這可以揭示系統(tǒng)涌現(xiàn)行為的深層次原理。這里有個非常關(guān)鍵的專業(yè)概念：對稱性破缺。專業(yè)的說法，“對稱性破缺是一個跨物理學(xué)、生物學(xué)、社會學(xué)與系統(tǒng)論等學(xué)科的概念，狹義簡單理解為對稱元素的喪失；也可理解為原來具有較高對稱性的系統(tǒng)，出現(xiàn)不對稱因素，其對稱程度自發(fā)降低的現(xiàn)象。”

想象一支鉛筆豎立在桌子上。鉛筆是對稱的——從所有平視角度看起來都一樣。但是，如果你敲打桌子，鉛筆會倒在一個方向上。這就破壞了鉛筆位置的對稱性，從不同的角度看起來它就不同了。

在物理學(xué)中，對稱性破缺也是一個類似的過程。一個系統(tǒng)可能具有對稱性，但如果經(jīng)歷了變化或干擾，它可能會打破對稱性，采取一個新的、不同的配置。“墨西哥帽”是對稱性破缺的常見教科書案例。

對稱性破缺的現(xiàn)象同樣也會出現(xiàn)在語言學(xué)習(xí)和大型語言模型中。在語言學(xué)習(xí)中，當(dāng)學(xué)習(xí)者遇到新的語言結(jié)構(gòu)或規(guī)則時，對稱性破缺現(xiàn)象可能就會發(fā)生。例如，如果一個以英語為母語的人開始學(xué)習(xí)漢語，他們最初可能會假設(shè)中文的句子結(jié)構(gòu)與英語類似。然而，他們很快就會發(fā)現(xiàn)中文的句子結(jié)構(gòu)是不同的，這一認識打破了他們關(guān)于語言的先前對稱性的假設(shè)。

大模型語言結(jié)晶

類似地，在像 GPT-3/4 這樣的大型語言模型中，當(dāng)模型在大規(guī)模數(shù)據(jù)集上進行訓(xùn)練并遇到新的、以前未見過的語言模式時，對稱性破缺現(xiàn)象也會發(fā)生。隨著模型遇到這些模式，它對語言的理解可能會發(fā)生變化和適應(yīng)，導(dǎo)致一種新的配置，打破了其語言空間剛剛建立的對稱性。

沒有預(yù)訓(xùn)練的Transformer是一張各向?qū)ΨQ的白紙，也就是其語言空間的密度函數(shù)ρ是均勻的。這個語言空間的密度函數(shù)決定了系統(tǒng)的信息熵，如果我們?nèi)匀话?ρ 表示成向量 η，則信息熵可以表示為F(η).隨著語料不斷被 emdedding 同時基于注意力機制 transform到這個語言空間，空間的密度ρ/η發(fā)生改變，信息熵 F(η)隨著改變，引發(fā)語言空間對稱性破缺與重建。這個過程可能會在局部區(qū)域不同尺度下持續(xù)的進行。一旦觸及臨界點，對稱性破缺引發(fā)相變，大模型就會在某些領(lǐng)域、不同長度上下文表現(xiàn)出各種神奇的涌現(xiàn)能力。

這里筆者借助對稱性破缺，解釋了 GPT 內(nèi)部語言概率空間的微擾，導(dǎo)致其語言空間對稱性的破缺，形成秩序，結(jié)成語言晶體。即語言概率空間的密度函數(shù)，向著更有序的方向相變。然而破缺可以隨機到一個相或另一個相，演化方向是很難預(yù)知的。這就凸顯了訓(xùn)練數(shù)據(jù)集的重要性，新引入的數(shù)據(jù)集會增加系統(tǒng)的對稱性，還是降低？即系統(tǒng)的信息熵增加還是降低？這些改變是整體還是局部進行？從目前GPT4 與GPT3的能力對比看，出現(xiàn)了整體大幅提升而局部降低的現(xiàn)象，或許是微擾導(dǎo)致局部特定尺度的破缺向更無序方向相變使然。

重整化群

對稱性普遍存在于各個尺度下的系統(tǒng)中，有對稱性的存在，就必然存在對稱性的破缺。重整化群（Renormalization Group) 是研究不同尺度下對稱性破缺與重建過程的核心數(shù)學(xué)手段。借助重整化群這一研究復(fù)雜物理系統(tǒng)行為的框架，人們可以在不同尺度上分析系統(tǒng)，并理解隨著觀察尺度的變化，系統(tǒng)的特性如何變化。通過這種方式，RG提供了一種研究微觀細節(jié)如何產(chǎn)生較大尺度新涌現(xiàn)特性的方法。