信號完整性分析是基于傳輸線理論的,研究信號完整性必須從認識傳輸線開始,而傳輸線中最基本的概念就是阻抗和反射。阻抗匹配和反射是信號完整性分析中最基本的問題。掌握好這一基本概念能夠幫助我們解釋實際測試、仿真應用中的各種信號完整性問題。
傳輸線的阻抗又有特征阻抗、瞬態阻抗、輸入阻抗三個概念,下文一一闡述。
01
傳輸線的特征阻抗
傳輸線的特征阻抗的定義為傳輸線上任意點處的電壓和電流的比值,上一節我們已經通過麥克斯韋方程的推導得出特征阻抗的計算公式。這里我不厭其煩還得把它再搬出來:
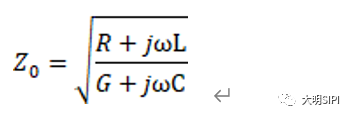
有了這個公式我們就可以簡化出傳輸線的RLCG模型:
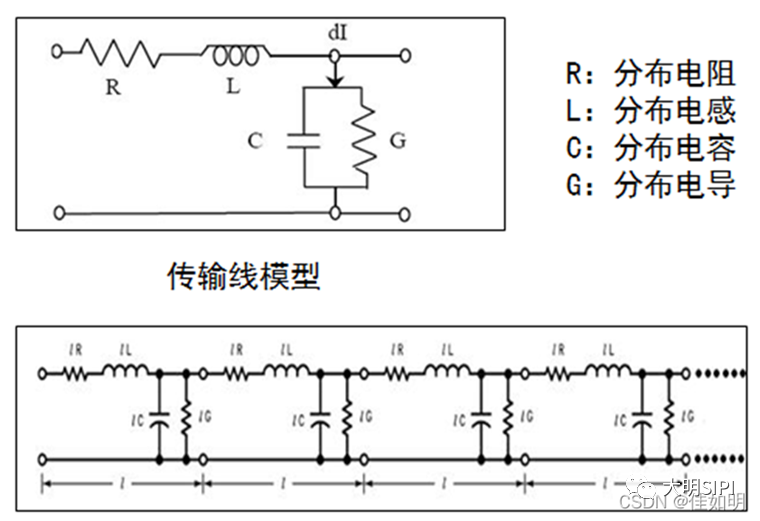
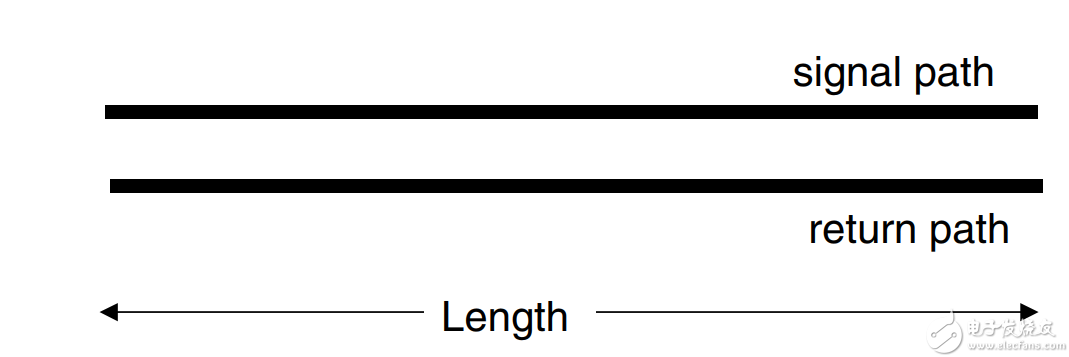
其中的R代表導體損耗;G代表了介質損耗。L代表傳輸線的分布電感,C代表信號路徑和返回路徑之間的分布電容。
02
傳輸線的瞬態阻抗
我們可以想象一下,信號有自己的感覺器官,它在傳輸線上傳輸的時候能夠感受到傳輸線阻抗的變化。像我們人一樣,能夠感受到腳下的路是平坦的道路還是坑坑洼洼的路。
信號在傳輸線上任一點所感受到的即時的阻抗就是瞬態阻抗。如果信號在傳輸線上的每一點感受到的阻抗都相同,那么我們就說傳輸線阻抗連續;反之,如果信號在傳輸線上感受到了阻抗變化,則說明傳輸線的阻抗不連續;信號在阻抗不連續點就會存在反射。
看到這里,有些讀者可能會有疑問了,傳輸線的瞬態阻抗和特征阻抗有什么關系呢?
瞬態阻抗是否就是特征阻抗 ?其實瞬態阻抗并不等于特征阻抗。要想瞬態阻抗=特征阻抗,需要有一個前提:傳輸線的長度要遠遠小于信號所包含頻譜的最小波長的1/4。
這個前提究竟有什么含義呢?簡單的理解也就是對于低速信號,瞬態阻抗可以近似等于特征阻抗。因為其信號頻譜的最高分量比較低因此波長會很大,此時傳輸線的長度有可能遠遠小于其波長的1/4。
為了解釋清楚這個問題,我們需要引入輸入阻抗的概念。
03
傳輸線的輸入阻抗
輸入阻抗的定義:信號在傳輸線上任意一點向負載端看過去的阻抗,用Z_in (z) 表示。
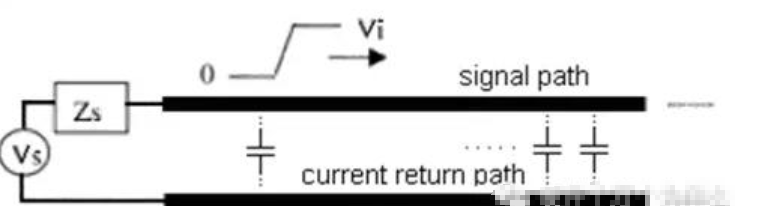
我們在推導傳輸線特征阻抗公式時,并沒有考慮端接的情況,是在無限長的平板傳輸線模型中進行的,但實際的傳輸線并非如此。如下圖所示是一個長度為“L”的傳輸線,其負載阻抗為,用小寫的字母“z”代表傳輸線上的位置。
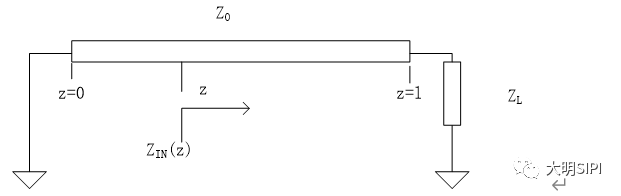
則可以推導出傳輸線的任意一點向負載方向看過去的輸入阻抗計算公式(這里省略推導過程,有興趣的讀者可以在電磁場與電磁波的書中找到答案):
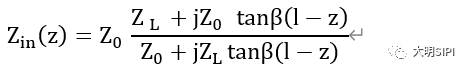
其中,
· 傳輸線長度為L;
· 為傳輸線的特征阻抗;
· β為相位,β=2π/λ;
· L-z為z點到終端的線長;
· 為傳輸線的終端阻抗。
由輸入阻抗公式可以看出:
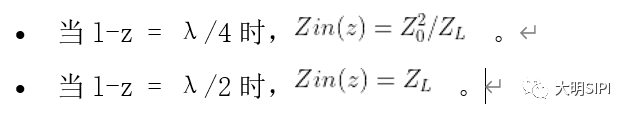
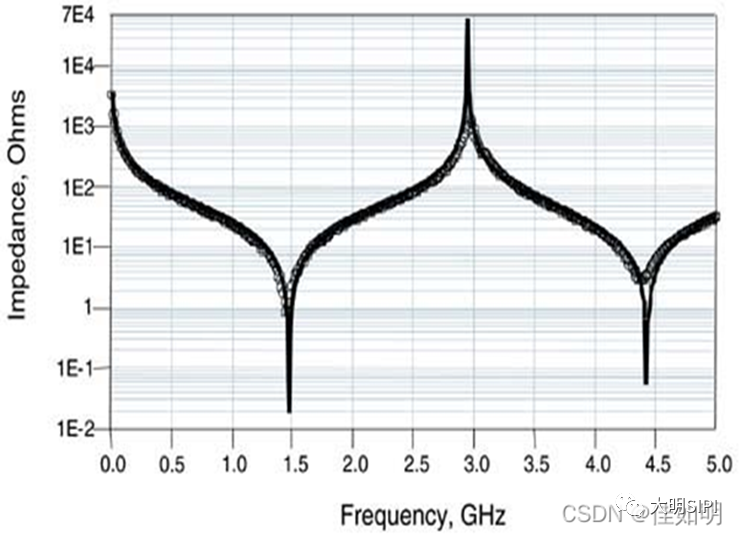
上圖為1in長、50Ω傳輸線的測量阻抗(圓圈)與仿真阻抗(線),可見線的輸入阻抗確實在隨著頻率的變化而變化。
我們討論一下z=0的情況(也就是信號輸入傳輸線的位置):
- 終端開路:ZL=∞,
o 當L=λ/4時,Zin(0)=0,輸入信號感受到的是短路;
o 當L=λ/2時,Zin(0)=ZL=∞, 輸入信號感受到的是開路。
- 終端短路:ZL=0,
o 當L=λ/4時,Zin(0)=∞,輸入信號感受到的是開路。
o 當L=λ/2時,Zin(0)=ZL=0,輸入信號感受到的是短路。
- 終端匹配:ZL=Z0,
o 當L=λ/4時,Zin(0)=Z0,輸入信號感受到的阻抗就是傳輸線特征阻抗;
o 當L=λ/2時,Zin(0)=ZL=Z0,輸入阻抗還是等于傳輸線特征阻抗。
由此,我們可以知道到傳輸線的負載端的端接阻抗和傳輸線阻抗不匹配時, 傳輸線的輸入阻抗或者信號在傳輸線上任一點感受到的阻抗都不是傳輸線的特征阻抗都是一個跟信號所處位置L、負載阻抗、特征阻抗相關的變量。
在沒有良好端接的情況下,就不能忽視傳輸線的長度帶來的影響。所以對于一些高速serdes大多采用CML電平,在發送和接收端都有端接來進行阻抗匹配。
-
接收器
+關注
關注
15文章
2563瀏覽量
73473 -
信號完整性
+關注
關注
68文章
1437瀏覽量
96490 -
電磁波
+關注
關注
21文章
1479瀏覽量
54469 -
電磁場
+關注
關注
0文章
799瀏覽量
47909 -
CML
+關注
關注
0文章
33瀏覽量
19819
發布評論請先 登錄
【連載筆記】信號完整性-傳輸線物理基礎及其分類
知識分享-傳輸線的返回電流(信號完整性揭秘)






 信號完整性(SIPI)學習—傳輸線的阻抗
信號完整性(SIPI)學習—傳輸線的阻抗
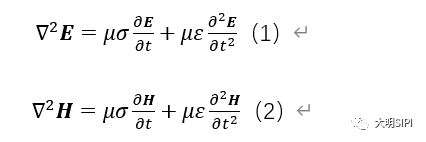











評論