1前言
S-Function是system-function系統(tǒng)函數(shù)的縮寫,是指采用非圖形化的方式描述的一個(gè)功能塊。S-Function提供給用戶自己編寫程序來滿足自己要求模型的接口。
2 s-function總體架構(gòu)
S-function包括主函數(shù)和6個(gè)子函數(shù),子函數(shù)包括
1.mdlInitializeSizes(初始化)
2.mdlDerivatives(連續(xù)狀態(tài)微分)
3.mdlUpdate(離散狀態(tài)更新)
4.mdlOutputs(模塊輸出)
5.mdlGetTimeOfNextVarHit(計(jì)算下次采樣時(shí)刻)
2.1 s-function 執(zhí)行過程
- 在仿真開始時(shí),執(zhí)行mdlInitializeSizes
- 若系統(tǒng)包含連續(xù)部分,則調(diào)用mdlDerivatives;若系統(tǒng)包含離散部分,則調(diào)用mdlUpdate
- 調(diào)用mdlOutputs,產(chǎn)生輸出
- 若滿足條件,則執(zhí)行mdlGetTimeOfNextVarHit
- 循環(huán)執(zhí)行1--3,直至仿真停止
- 執(zhí)行mdlTerminate,仿真停止
2.2 s-function 輸入輸出參數(shù)與狀態(tài)變量
function [sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag)
S-function是基于狀態(tài)空間表達(dá)式而設(shè)置的仿真模塊,需要了解這個(gè)仿真模塊的輸入輸出和內(nèi)部的狀態(tài)變量。
輸入變量:
t :系統(tǒng)時(shí)間
x :系統(tǒng)狀態(tài)
u : 系統(tǒng)輸入,即在simulink models中連接至S-function的線上的數(shù)據(jù)。注意區(qū)分x和u
flag : 系統(tǒng)狀態(tài),由系統(tǒng)自動(dòng)生成,決定了系統(tǒng)應(yīng)當(dāng)執(zhí)行哪個(gè)S-function子函數(shù)
除了這四個(gè)必須有的變量,還可以自行根據(jù)需要添加變量,供子函數(shù)調(diào)用
輸出變量:
sys : 系統(tǒng)本身,可以理解為下一時(shí)刻的系統(tǒng);同時(shí)sys的前幾個(gè)數(shù)值(sys[1]等)是系統(tǒng)的輸出,即在simulink中S-function伸出線上的數(shù)據(jù)
x0 : 系統(tǒng)初始狀態(tài)
str : 狀態(tài)排序字符串,通常指定為[]。
ts : 可認(rèn)為是采樣時(shí)間
(simStateCompliance 不用管)
3 子函數(shù)
3.1 mdlInitializeSizes函數(shù)
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
% 不需要更改的內(nèi)容
sizes = simsizes;
% 需要更改的內(nèi)容:狀態(tài)、輸出、輸入的數(shù)量
sizes.NumContStates = 0; %連續(xù)狀態(tài)的數(shù)量
sizes.NumDiscStates = 0; %離散狀態(tài)的數(shù)量
sizes.NumOutputs = 0; %輸出的數(shù)量
sizes.NumInputs = 0; %輸入的數(shù)量
sizes.DirFeedthrough = 1; %輸出y和輸入u是否是直通(輸出的向量中是否直接含有輸入)
sizes.NumSampleTimes = 1; %采樣時(shí)間
sys = simsizes(sizes);
% 需要更改的內(nèi)容:狀態(tài)變量的初始值
x0 = [];
% 不需要更改的內(nèi)容
str = [];
% 按需要更改,ts的第一個(gè)數(shù)字表示采樣時(shí)間,第二個(gè)數(shù)字表示偏移量;連續(xù)系統(tǒng)不需要改
% [0 0]——表示默認(rèn)采樣時(shí)間(默認(rèn)為0.2秒采樣一次);
% [-1 0] ——表示根據(jù)連接模塊的采樣頻率進(jìn)行采樣;
ts = [0 0];
% 按需要更改
simStateCompliance = 'UnknownSimState';
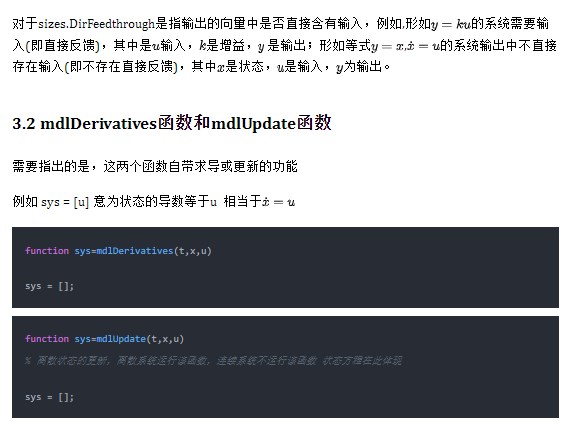
3.3 mdlOutputs函數(shù)
function sys=mdlOutputs(t,x,u)
sys = [];
3.4 mdlGetTimeOfNextVarHit函數(shù)
function sys=mdlGetTimeOfNextVarHit(t,x,u)
% 計(jì)算下一個(gè)采樣點(diǎn)的絕對(duì)時(shí)間,只有當(dāng)在mdlInitializeSizes中指定了變步長(zhǎng)離散采樣時(shí)間時(shí),才使用該程序
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
3.5 mdlTerminate函數(shù)
function sys=mdlTerminate(t,x,u)
% 終止函數(shù),可添加當(dāng)Simulink終止時(shí)所需執(zhí)行內(nèi)容
sys = [];
4 舉例
4.1 二階模型
對(duì)于如下被控對(duì)象,其傳遞函數(shù)為:


仿真結(jié)果:曲線重合,三種模型表達(dá)方式相同

4.2 簡(jiǎn)單自適應(yīng)控制系統(tǒng)(MRAC)
4.2.1 系統(tǒng)模型與證明


s-function input
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 3;
sizes.NumInputs = 0;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0 = [0.5,0];
str = [];
ts = [];
function sys=mdlDerivatives(t,x,u)
r=sin(4*t);
nmn1=10;
nmn2=25;
sys(1)=x(2);
sys(2)=-nmn1*x(2)-nmn2*x(1)+nmn2*r;
function sys=mdlOutputs(t,x,u)
r=sin(4*t);
nmn1=10;
nmn2=25;
xm=x(1);
dxm=x(2);
ddxm=-nmn1*x(2)-nmn2*x(1)+nmn2*r;
sys(1)=xm;
sys(2)=dxm;
sys(3)=ddxm;
s-function controller
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 1;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 6;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0 = [0];
str = [];
ts = [];
function sys=mdlDerivatives(t,x,u)
xm=u(1);
dxm=u(2);
ddxm=u(3);
x1=u(4);
dx1=u(5);
e=x1-xm;
de=dx1-dxm;
nmn=6;
s=de+nmn*e;
v=ddxm-2*nmn*de-nmn^2*e;
gama=0.5;
sys(1)=-gama*v*s;
function sys=mdlOutputs(t,x,u)
xm=u(1);
dxm=u(2);
ddxm=u(3);
x1=u(4);
dx1=u(5);
e=x1-xm;
de=dx1-dxm;
nmn=6;
mp=x(1);
ut=mp*(ddxm-2*nmn*de-nmn^2*e);
sys(1)=mp;
sys(2)=ut;
s-function plant
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 3;
sizes.NumInputs = 2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [0.5,0];
str = [];
ts = [0 0];
function sys=mdlDerivatives(t,x,u)
m=2;
ut=u(2);
sys(1)=x(2);
sys(2)=1/m*ut;
function sys=mdlOutputs(t,x,u)
m=2;
sys(1)=x(1);
sys(2)=x(2);
sys(3)=m;
理想位置輸出與真實(shí)位置輸出

參數(shù)m估計(jì)值與真實(shí)值

-
仿真器
+關(guān)注
關(guān)注
14文章
1036瀏覽量
85312 -
狀態(tài)機(jī)
+關(guān)注
關(guān)注
2文章
493瀏覽量
28207 -
MRAC
+關(guān)注
關(guān)注
0文章
4瀏覽量
7217
發(fā)布評(píng)論請(qǐng)先 登錄
無模型自適應(yīng)控制在永磁同步電機(jī)轉(zhuǎn)速中的仿真研究
s-function的概念
建立m文件s-function
橫潤(rùn)科技《MATLAB的S-Function編寫指導(dǎo)
搭建最基本的S-function模塊
simulink仿真問題:s_function
什么是s-function
如何去實(shí)現(xiàn)S-Function與Simulink的數(shù)據(jù)交互呢
基于MATLAB的時(shí)變系統(tǒng)自適應(yīng)控制的仿真
基于MATLAB S-Function的飛行器運(yùn)動(dòng)系統(tǒng)建模與
MATLAB的S-Function編寫指導(dǎo)
SIMULINK s-function的設(shè)計(jì)
使用Simulink進(jìn)行S-Function建模的教程PPT課件免費(fèi)下載
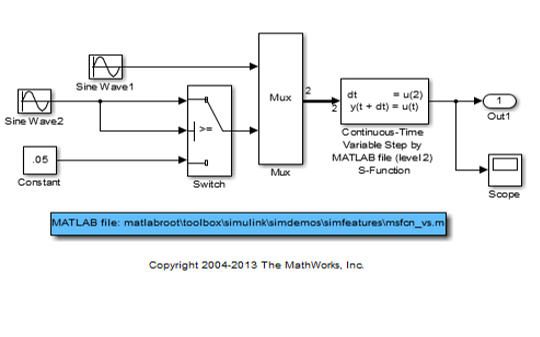





 S-function詳解與模型參考自適應(yīng)仿真案例
S-function詳解與模型參考自適應(yīng)仿真案例











評(píng)論