消卷積是一種提高光學(xué)顯微圖像對比度和清晰度的基于大量計算的圖像處理技術(shù)。除非空間兩點彼此之間的距離超過波長半峰寬，否則光學(xué)顯微鏡因衍射極限而無法分辨單一結(jié)構(gòu)。低于該衍射極限的每個點源都會被顯微鏡模糊成所謂的點擴散函數(shù)（PSF）。使用傳統(tǒng)的寬場熒光顯微鏡，焦平面上方或下方區(qū)域的非焦面光線會導(dǎo)致所采集的圖像更加模糊。消卷積通過利用光學(xué)系統(tǒng)的點擴散函數(shù)以及重建由較小點源集合構(gòu)成的理想圖像的方式消除或逆轉(zhuǎn)這一問題。 光學(xué)顯微鏡的點擴散函數(shù)會根據(jù)顯微鏡和樣品的光學(xué)特性而發(fā)生變化，因此很難通過實驗確定整個系統(tǒng)準確的點擴散函數(shù)。為此已經(jīng)開發(fā)出用于確定點擴散函數(shù)的數(shù)學(xué)算法，并通過消卷積方法進行最佳重建獲得理想圖像。使用熒光顯微鏡采集的包括非三維圖像在內(nèi)幾乎所有圖像均可以進行消卷積。 商業(yè)軟件把這類算法整合到更具成本效益的用戶友好的程序包中使用。每種消卷積算法在確定卷積運算的點擴散和噪聲函數(shù)方面均有所不同。

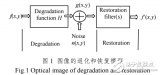
基本成像公式為：g(x) = f(x) * h(x) + n(x)

x: 空間坐標
g(x): 所觀察圖像
f(x): 目標

h(x): 點擴散函數(shù)
n(x): 噪聲函數(shù)
*：卷積

01

去模糊算法

去模糊算法對三維圖像堆棧的每個二維平面進行操作。最近鄰算法是最常見的去模糊技術(shù)，其通過模糊相鄰平面（使用數(shù)字模糊濾波器的z + 1和z-1）對每個z平面進行操作，然后從z平面減去模糊平面。多近鄰算法將這一概念擴展到用戶可選擇的多個平面。通過將算法應(yīng)用于堆棧中的每個平面對三維堆棧進行處理。

由于只是在少量圖像平面上執(zhí)行相對簡單的計算，這類去模糊算法在計算上具有經(jīng)濟性（快速）。但是，這些方法存在一些缺點。例如，其點擴散函數(shù)在附近的z平面彼此重疊，因此點擴散函數(shù)可能有信號來源于不屬于它們的平面上，從而更改變對象的外觀位置。在對單個二維圖像進行去模糊處理時，這一問題尤為嚴重，因為通常衍射斑或非焦結(jié)構(gòu)發(fā)出的光被作為當前焦平面中的信號而銳化。

02

逆濾波器算法

逆濾波器通過對圖像進行傅立葉變換并將其除以點擴散函數(shù)的傅立葉變換而發(fā)揮作用。傅立葉空間中的除法等效于現(xiàn)實空間中的消卷積，這使得逆濾波成為逆轉(zhuǎn)圖像卷積最簡單的方法。其計算速度快，速度與二維去模糊方法相仿。但是，這一方法的實用性受到噪聲放大的限制。在傅立葉空間中進行分割時，通過除法運算會放大傅立葉變換中的微小噪聲變化。其結(jié)果是模糊消除與噪聲增益相折衷。該技術(shù)還可能引入稱為ringing的偽影。

通過對產(chǎn)生圖像的物體結(jié)構(gòu)進行某些假設(shè)，可以減少額外的噪聲和ringing。比如，如果假定對象相對平滑，則可消除具有粗糙邊緣的噪聲。正則化可在逆濾波器中一步執(zhí)行，也可以迭代應(yīng)用。其結(jié)果為去除高頻傅立葉的圖像，從而讓外觀更平滑。圖像中去除的大部分“粗糙度”均位于傅立葉頻譜上，而該頻率遠遠超出分辨率極限，因此該過程無法消除顯微鏡所記錄的結(jié)構(gòu)。但是，由于存在丟失細節(jié)的可能性，因此逆濾波器的軟件實現(xiàn)通常提供可調(diào)整的參數(shù)，讓用戶能夠在控制平滑和噪聲放大之間的取舍。在大多數(shù)圖像處理軟件程序中，這些算法存在多種名稱，其中包括維納消卷積、正則化最小二乘、線性最小二乘和Tikhonov-Miller正則化。

03

受限迭代算法

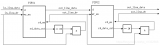
典型的受限迭代算法通過應(yīng)用額外算法將光子恢復(fù)到正確位置并提高逆濾波器的性能。這些方法基于上一循環(huán)結(jié)果以連續(xù)方式運行，因此稱為迭代。首先對對象進行初始估計，并與點擴散函數(shù)進行卷積。將所得的“模糊估計”與原始圖像進行比較，以此計算出一個代表模糊估計與原始圖像的相似程度的誤差標準。使用包含在誤差標準中的信息進行新的迭代-將新的估計值與點擴散函數(shù)卷積在一起，再計算出新的誤差標準，依此類推。最佳結(jié)果是盡可能減小誤差標準的估計。隨著算法的循環(huán)，每次軟件確定誤差標準尚未最小化時，新的估計值就會再次模糊，并重新計算誤差標準。重復(fù)該循環(huán)，直到將誤差標準最小化或達到所規(guī)定的閾值為止。最終還原的圖像為最后一次迭代時的對象估計。

受限迭代算法可提供良好的結(jié)果，但并不適合所有成像設(shè)置。其需要較長的計算時間，并且對計算機處理器要求很高。這些可以通過現(xiàn)代技術(shù)來克服，比如基于GPU的處理可以顯著提高速度。為了充分利用算法，需要三維圖像，盡管二維圖像也可以獲得有限的性能。

04

共聚焦、多光子和超分辨率

有人認為可以將消卷積作為共聚焦顯微鏡的替代術(shù)。嚴格上講并非如此，因為消卷積技術(shù)也可應(yīng)用于共聚焦顯微鏡圖像。實際上，消卷積可以恢復(fù)共聚焦、多光子或超分辨率光學(xué)顯微鏡圖像。

通過共聚焦或超分辨率顯微鏡和消卷積技術(shù)共同改善光學(xué)圖像所實現(xiàn)的清晰度提升超出了單獨使用這兩種技術(shù)所達到的效果。但是，對這些專用顯微鏡圖像進行消卷積的主要好處是可以減少最終圖像中的噪聲。這對于活細胞超分辨率或共聚焦成像等弱光應(yīng)用特別有用。多光子圖像的消卷積也已成功用于消除噪聲和提高對比度。在任何情況下，均需注意使用適當?shù)狞c擴散函數(shù)，尤其是在共聚焦針孔孔徑可調(diào)的情況下。

*1.Shaw, Peter J., 和David J. Rawlins。共焦顯微鏡的點擴散函數(shù)：其測量以及在3-D數(shù)據(jù)消卷積中的使用。J.ournal of Microscopy。163，第2期（1991）：151–165.

05

實踐中的消卷積

軟件實現(xiàn)消卷積算法的方式會極大影響處理速度和質(zhì)量。可以對算法進行優(yōu)化，以減少迭代次數(shù)并加速收斂，以生成穩(wěn)定的估計值。例如，未優(yōu)化的Jansson-Van Cittert算法通常需要50到100次迭代才能收斂到最佳估計值。通過對原始圖像進行預(yù)濾波以抑制噪聲并在前兩次迭代中使用附加誤差標準進行校正，該算法可收斂到僅5至10次迭代。

當使用實驗測得點擴散函數(shù)時，使用噪聲最小的高質(zhì)量點擴散函數(shù)至關(guān)重要。為達到這一目的，商業(yè)軟件中包含有可通過對點擴散函數(shù)的傅里葉變換求平均值的方式減少噪聲并增強徑向?qū)ΨQ性的預(yù)處理算法。很多軟件包還在點擴散函數(shù)中強制執(zhí)行軸對稱，并假定沒有球差。這些步驟減少了實驗點擴散函數(shù)的噪聲和像差，并在修復(fù)質(zhì)量上產(chǎn)生顯著差異。

預(yù)處理還可對原始圖像使用諸如背景減除和平場校正之類的算法。這些操作可以改善信噪比并消除某些對最終圖像有害的偽影。

通常，數(shù)據(jù)重構(gòu)結(jié)果還原度越高，消卷積圖像所需的計算機內(nèi)存和處理器時間就越多。以往，為適應(yīng)處理能力，圖像會被細分為多個子集 ，但是現(xiàn)代技術(shù)已經(jīng)消除這一問題，并擴展為更大的數(shù)據(jù)集。

審核編輯：黃飛