微變等效電路法(Small-Signal Equivalent Circuit Method)是一種在電子電路分析中常用的方法,特別是在模擬電路設計和分析中。它主要用于分析電路在小信號激勵下的動態行為。
微變等效電路法概述
1. 引言
在電子電路設計和分析中,了解電路在不同工作條件下的行為至關重要。微變等效電路法是一種分析電路在小信號激勵下動態行為的有效工具。本文將詳細介紹微變等效電路法的基本原理、應用場景、分析方法和實際應用。
2. 微變等效電路法的基本原理
2.1 基本概念
微變等效電路法基于線性化原理,將非線性電路在工作點附近線性化,以便于分析和計算。這種方法適用于分析電路在小信號激勵下的動態行為,如增益、相位、頻率響應等。
2.2 線性化過程
線性化過程包括以下幾個步驟:
- 確定工作點:在電路的靜態工作條件下,確定電路中各個元件的工作點,如晶體管的偏置電壓和電流。
- 線性化元件:將非線性元件(如晶體管、二極管等)在工作點附近線性化,用線性電阻、電容等元件代替。
- 建立等效電路:根據線性化后的元件,建立電路的微變等效電路。
2.3 微變等效電路的特點
微變等效電路具有以下特點:
- 線性:電路中的元件都是線性元件,便于分析和計算。
- 局部性:微變等效電路只考慮電路在工作點附近的小信號行為,忽略了大信號下的非線性效應。
- 近似性:微變等效電路是對實際電路的近似描述,可能存在一定的誤差。
3. 微變等效電路法的應用場景
微變等效電路法廣泛應用于以下領域:
- 模擬電路設計:在模擬電路設計中,微變等效電路法用于分析電路的放大倍數、帶寬、穩定性等性能指標。
- 信號處理:在信號處理領域,微變等效電路法用于分析濾波器、振蕩器等電路的頻率響應特性。
- 電路故障診斷:微變等效電路法可以用于分析電路的故障原因,如增益下降、相位失真等。
- 電路優化:通過微變等效電路法分析電路的性能,可以對電路進行優化設計,提高電路的性能和可靠性。
4. 微變等效電路法的分析方法
4.1 節點分析法
節點分析法是一種基于基爾霍夫電流定律的電路分析方法。在微變等效電路中,可以列出各個節點的電流方程,然后求解電路的響應。
4.2 環路分析法
環路分析法是一種基于基爾霍夫電壓定律的電路分析方法。在微變等效電路中,可以列出各個環路的電壓方程,然后求解電路的響應。
4.3 頻率響應分析
頻率響應分析是分析電路在不同頻率下的響應特性,如增益、相位、帶寬等。在微變等效電路中,可以通過拉普拉斯變換將時域分析轉換為頻域分析。
4.4 穩定性分析
穩定性分析是評估電路在不同工作條件下的穩定性,如增益裕度、相位裕度等。在微變等效電路中,可以通過開環增益和閉環增益的計算來評估電路的穩定性。
5. 微變等效電路法的實際應用
5.1 放大器設計
在放大器設計中,微變等效電路法用于分析放大器的增益、帶寬、線性度等性能指標。通過優化電路參數,可以設計出高性能的放大器。
5.2 濾波器設計
在濾波器設計中,微變等效電路法用于分析濾波器的頻率響應特性,如截止頻率、帶寬、帶內波動等。通過調整電路參數,可以設計出滿足特定要求的濾波器。
5.3 振蕩器設計
在振蕩器設計中,微變等效電路法用于分析振蕩器的振蕩頻率、幅度穩定性等性能指標。通過優化電路參數,可以設計出高性能的振蕩器。
-
模擬電路
+關注
關注
125文章
1591瀏覽量
103813 -
元件
+關注
關注
4文章
1168瀏覽量
37568 -
電子電路
+關注
關注
78文章
1244瀏覽量
67815 -
微變等效電路
+關注
關注
5文章
14瀏覽量
6417
發布評論請先 登錄
晶體管的微變等效電路相關資料分享
微變等效電路法有哪些巧用
如何一秒學會畫微變等效電路?(等效電路畫圖技巧)
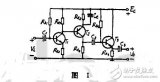
共射放大電路的微變等效電路分析詳情
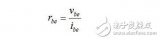





 微變等效電路法適用于什么
微變等效電路法適用于什么













評論