在圖形用戶界面(GUI)設計中,自定義連線技術不僅提升了用戶體驗,還為復雜數據可視化開辟了新的可能性。該功能點允許用戶靈活地在界面元素之間創建視覺連接,使流程圖、思維導圖和網絡拓撲圖等信息呈現更加直觀和動態。
圖撲軟件自研 HT for Web 產品框架中,ht.Edge 節點用于表示節點間的連線關系。熟悉 HT 的用戶應該了解 ht.Edge 內置了多種連線類型,能滿足一般拓撲圖需求,但在特殊情況下,這些默認類型可能無法滿足需求。為此,HT 提供了自定義連線功能,允許開發者根據具體需求創建特殊的連線類型,實現更靈活的圖形表示。
自定義連線
圖撲 HT 框架提供靈活的自定義連線功能,開發者可以通過調用 ht.Default.setEdgeType(type, func, mutual) 方法來創建獨特的連線類型。以下是該方法的參數詳解:
■type:自定義連線類型的名稱,與 style 中的 edge.type 屬性相對應。
■func:計算連線路徑信息的函數,接收四個參數:
gap:多條連線成捆時,本連線對象對應中心連線的間距。
edge:當前連線對象。
graphView:當前對應拓撲組件對象。
sameSourceWithFirstEdge:boolean 類型,該連線是否與同組的第一條連線同源。
■mutual:決定該連線類型是否會影響同一起始或結束節點上的其他連線。
接下來,我們深入分析一種常見的拓撲關系實現步驟,即"橫-豎-橫"的連線方式。
下面是一段定義上圖連線類型的示例代碼。代碼很簡單,首先獲取起始節點和目標節點的信息,然后根據這兩個節點的坐標,按照預定的規則計算出連線的路徑點。
ht.Default.setEdgeType('horizontal-vertical', function (edge, gap, graphView) {
const points = new ht.List();
const segments = new ht.List();
const source = edge.getSource();
const target = edge.getTarget();
const sourceP = source.p();
const targetP = target.p();
points.add(sourceP);
if (targetP.x !== sourceP.x) {
points.add({ x: sourceP.x + (targetP.x - sourceP.x) / 2, y: sourceP.y });
points.add({ x: sourceP.x + (targetP.x - sourceP.x) / 2, y: targetP.y });
}
points.add(targetP);
return { points, segments };
})
定義好連線類型后,只需通過 edge.s('edge.type', 'horizontal-vertical') 這段簡單的代碼行,就能將 edge 對象的連線設置為我們剛剛定義的類型。由此一來,即可看到令人滿意的效果,大幅提升圖形的可讀性和美觀度。
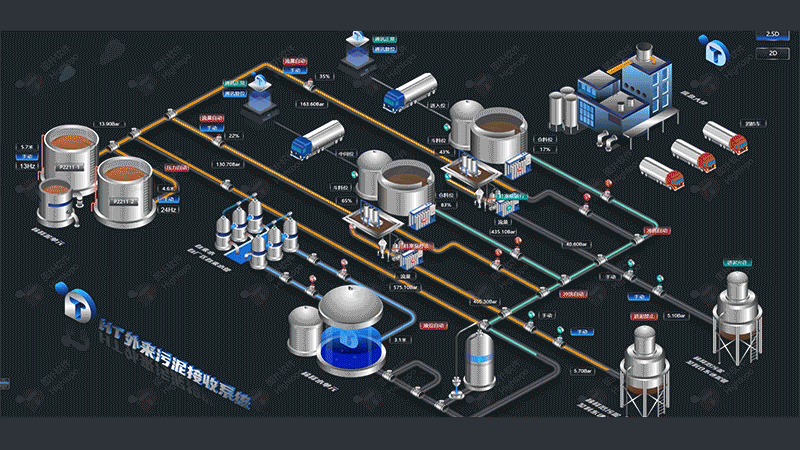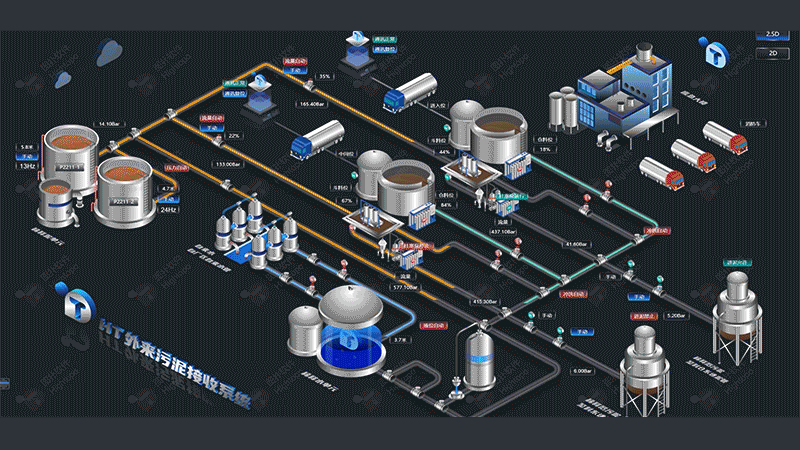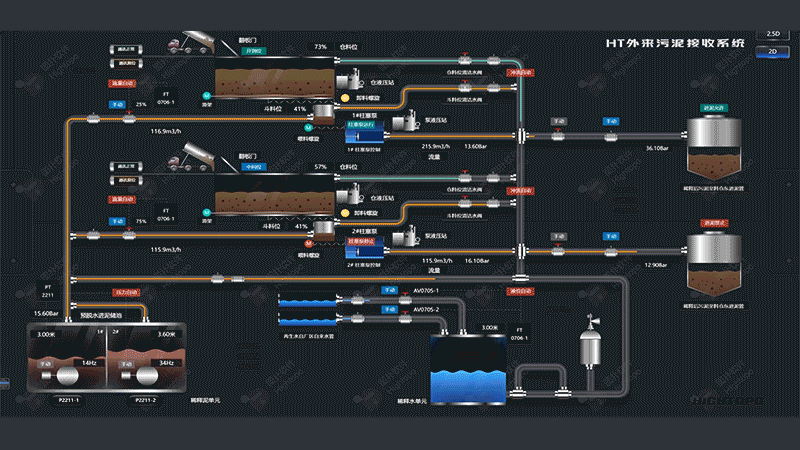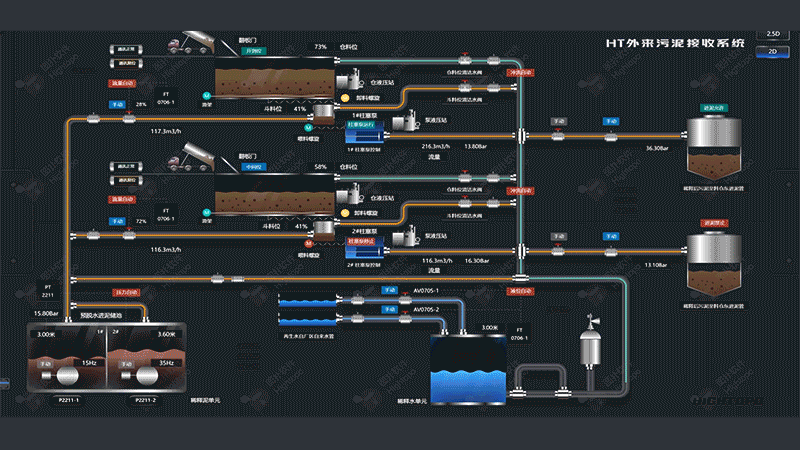
總線拓撲
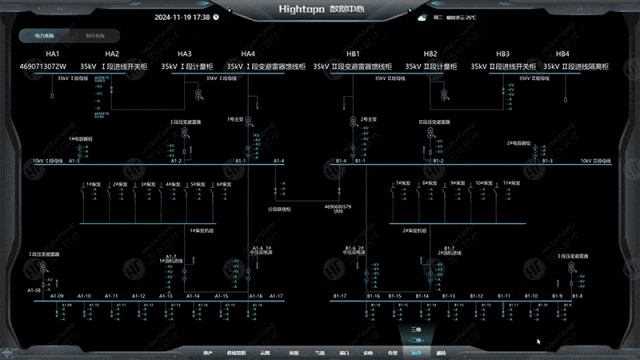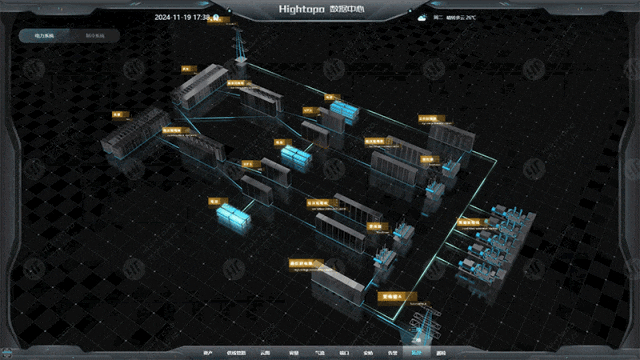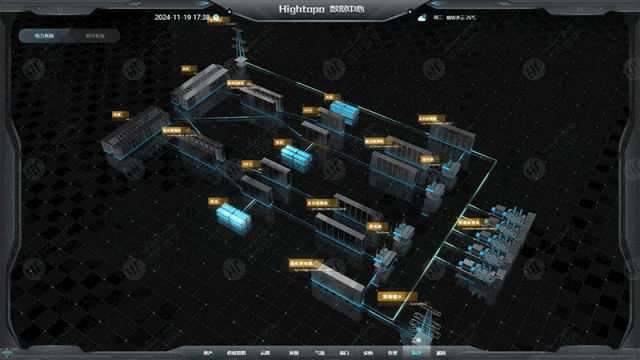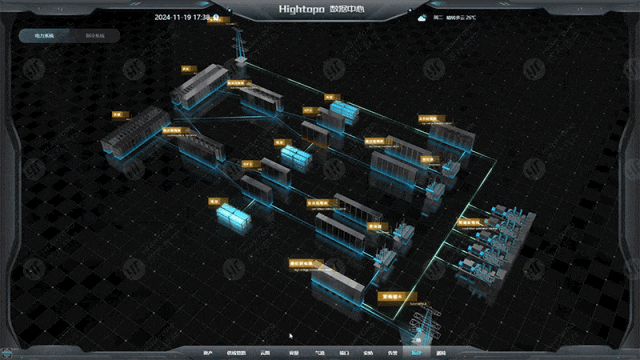
總線拓撲是一種網絡結構,所有設備(如計算機、打印機等)都連接到一個共同的通信介質上,通常是一根電纜,這個介質被稱為"總線"(bus)。總線拓撲在工業控制和嵌入式系統等特定領域中被廣泛應用。在圖撲 HT 框架中,我們可以利用 ht.Shape 組件繪制總線,并通過 ht.Edge 組件將各個設備節點連接到總線上。這些連接的視覺表現可通過自定義連線類型靈活定義,從而實現精確的總線拓撲圖表示。
上面展示的是一個總線的示例效果,可以直觀看到所有設備都連接到了總線上。在具體實現過程中,最具挑戰性的問題是:如何計算出總線上距離目標節點坐標最近的點?
計算節點到總線距離
總線通常由多條直線段組成,因此計算某一節點到總線的最短距離可按以下思路進行:
將總線分割為多段直線
總線由多個直線段構成,可以取總線上相鄰兩點構成一條直線。具體實現時,遍歷 points 數據,獲取 points[index] 和 points[index+1] 作為線段的兩個端點。注意,如果設置了 segments,其中 1 代表新路徑的起點,所以當 segments[index+1] 為 1 時應跳過。
計算點到每條直線的距離
獲取每條直線段后,計算節點坐標到各線段的距離,并將距離值存入一個集合中。
獲取最短距離
從距離集合中找出最小值,即為節點到總線的最短距離。
基于上述思路,我們可以實現一個總線連線類型。以下是具體的實現代碼:
// 計算點到直線的距離,返回結果是個對象結構
var pointToInsideLine = function (p1, p2, p) {
var x1 = p1.x,
y1 = p1.y,
x2 = p2.x,
y2 = p2.y,
x = p.x,
y = p.y,
result = {},
dx = x2 - x1,
dy = y2 - y1,
d = Math.sqrt(dx * dx + dy * dy),
ca = dx / d, // cosine
sa = dy / d, // sine
mX = (-x1 + x) * ca + (-y1 + y) * sa;
result.x = x1 + mX * ca;
result.y = y1 + mX * sa;
if (!isPointInLine(result, p1, p2)) {
result.x = Math.abs(result.x - p1.x) < Math.abs(result.x - p2.x) ? p1.x : p2.x;
result.y = Math.abs(result.y - p1.y) < Math.abs(result.y - p2.y) ? p1.y : p2.y;
}
dx = x - result.x;
dy = y - result.y;
result.z = Math.sqrt(dx * dx + dy * dy);
return result;
};
// 判斷點是否在線上
var isPointInLine = function (p, p1, p2) {
return p.x >= Math.min(p1.x, p2.x) &&
p.x <= Math.max(p1.x, p2.x) &&
p.y >= Math.min(p1.y, p2.y) &&
p.y <= Math.max(p1.y, p2.y);
};
// 注冊連線類型
ht.Default.setEdgeType('bus', function (edge) {
var source = edge.getSourceAgent(),
target = edge.getTargetAgent();
var targetP = target.p();
var points = source.getPoints().toArray();
var segments = source.getSegments();
var beginPoint;
for (let i = 0; i < points.length - 1; i++) {
if (segments) {
if (segments[i + 1] === 1) continue;
}
const point1 = points[i];
const point2 = points[i + 1];
const minPosition = pointToInsideLine(point1, point2, targetP);
if (!beginPoint || minPosition.z < beginPoint.z) {
beginPoint = minPosition;
}
}
return {
points: new ht.List([ beginPoint, targetP ]),
segments: new ht.List([1, 2])
};
});
執行上述代碼后,我們將得到如下效果:
從上圖可以清楚看出,示例成功獲取了節點到總線的最近點,并繪制了相應的連線節點。值得注意的是,對于直線段而言,節點在直線上的投影點即為其距總線最近的點。
視覺美感優化
雖然示例已實現了基礎總線效果,但由于拓撲圖采用 2.5D 效果,僅計算投影點可能無法呈現理想的視覺效果。為了增強視覺表現,我們可以考慮讓連線旋轉一定角度。為此,我們可以在現有功能的基礎上添加旋轉代碼,使連線與整體圖形更加協調,提升視覺美感。
ht.Default.setEdgeType('bus', function (edge) {
var source = edge.getSourceAgent(),
target = edge.getTargetAgent();
var targetP = target.p();
var points = source.getPoints().toArray();
var segments = source.getSegments();
var beginPoint, linePoints;
for (let i = 0; i < points.length - 1; i++) {
if (segments) {
if (segments[i + 1] === 1) continue;
}
const point1 = points[i];
const point2 = points[i + 1];
const minPosition = pointToInsideLine(point1, point2, targetP);
if (!beginPoint || minPosition.z < beginPoint.z) {
beginPoint = minPosition;
linePoints = [point1, point2]
}
}
var rotation = angleBetweenLineAndHorizontal(linePoints[0], linePoints[1]);
var rotatePoint = findIntersection([rotatePointAroundAnotherPoint(beginPoint, targetP, rotation), targetP], linePoints);
if(isPointInLine(rotatePoint, linePoints[0], linePoints[1])){
beginPoint = rotatePoint;
}
return {
points: new ht.List([
beginPoint, targetP
]),
segments: new ht.List([1, 2])
};
});
/**
* 計算兩點之間直線與水平線的夾角
*/
function angleBetweenLineAndHorizontal(p1, p2) {
if (new ht.Math.Vector2(p1.x, p1.y).length() > new ht.Math.Vector2(p2.x, p2.y).length()) {
var p = p2;
p2 = p1;
p1 = p;
}
var x1 = p1.x,
y1 = p1.y,
x2 = p2.x,
y2 = p2.y;
var dx = x2 - x1;
var dy = y2 - y1;
var angleRadians = Math.atan2(dy, dx); // 計算夾角(弧度)
var angleDegrees = angleRadians * (180 / Math.PI); // 弧度轉角
// 確保角度在 0 到 360 之間
if (angleDegrees < 0) {
angleDegrees += 360;
}
return angleDegrees;
}
function rotatePointAroundAnotherPoint(point, center, angleDegrees) {
var angleRadians = angleDegrees * (Math.PI / 180);
var cosTheta = Math.cos(angleRadians);
var sinTheta = Math.sin(angleRadians);
var translatedX = point.x - center.x;
var translatedY = point.y - center.y;
var rotatedX = translatedX * cosTheta - translatedY * sinTheta;
var rotatedY = translatedX * sinTheta + translatedY * cosTheta;
var finalX = rotatedX + center.x;
var finalY = rotatedY + center.y;
return { x: finalX, y: finalY };
}
/**
* 給定兩個點,計算直線的系數 A, B, C
* 直線方程:Ax + By = C
*/
function getLineEquation(x1, y1, x2, y2) {
var A = y2 - y1;
var B = x1 - x2;
var C = A * x1 + B * y1;
return { A, B, C };
}
/**
* 計算兩條直線的交點
*/
function calculateIntersection(line1, line2) {
var { A: A1, B: B1, C: C1 } = line1;
var { A: A2, B: B2, C: C2 } = line2;
var determinant = A1 * B2 - A2 * B1;
if (determinant === 0) {
// 平行或重合
return null;
} else {
var x = (C1 * B2 - C2 * B1) / determinant;
var y = (A1 * C2 - A2 * C1) / determinant;
return { x, y };
}
}
/**
* 找到兩條線的交點,或者延長線的交點
*/
function findIntersection(line1Points, line2Points) {
var [p1, p2] = line1Points;
var [p3, p4] = line2Points;
var line1 = getLineEquation(p1.x, p1.y, p2.x, p2.y);
var line2 = getLineEquation(p3.x, p3.y, p4.x, p4.y);
var intersection = calculateIntersection(line1, line2);
return intersection;
}
實現的最終效果如下:
圖撲軟件 HT 自定義連線功能為圖形交互設計開辟了廣闊的新天地。從基本的"橫-豎-橫"連線到復雜的總線拓撲圖,不僅提升了數據可視化的靈活性,還大幅增強了用戶體驗。通過精細調整連線的旋轉角度和投影點,在 2.5D 效果中呈現更加美觀和直觀的拓撲關系。
不僅適用于網絡結構的展示,還可擴展到各種復雜系統的可視化中。為設計師和開發者提供了強大的工具,幫助他們創造出更加豐富、富有表現力的圖形界面。
審核編輯 黃宇
-
拓撲圖
+關注
關注
1文章
20瀏覽量
14667 -
數據可視化
+關注
關注
0文章
476瀏覽量
10805
發布評論請先 登錄
基于 HT 的 3D 可視化智慧礦山開發實現

如何使用協議分析儀進行數據分析與可視化
可視化組態物聯網平臺是什么
基于圖撲 HT 技術的電纜廠 3D 可視化管控系統深度解析
基于 HT 2D&3D 渲染引擎的新能源充電樁可視化運營系統技術剖析

VirtualLab Fusion中的可視化設置
VirtualLab Fusion應用:光波導k域布局可視化(“神奇的圓環”)
七款經久不衰的數據可視化工具!
智慧能源可視化監管平臺——助力可視化能源數據管理

HT for Web并力ARMxy工業計算機實現數字化轉型可視化解決方案






 圖撲 HT 總線式拓撲圖的可視化實現
圖撲 HT 總線式拓撲圖的可視化實現














評論