細思極恐
既然圓周率是無限不循環小數,那么其中是否可能包括這個世界上可用數字描述的任何信息,也就是包含了這個世界?
電話號, 生日, QQ號可能運算量比較大,但是6位的銀行卡密碼還是沒問題的。題目本身和Pi是不是正規數沒關系,但假如承認 Pi 是個正規數會有幫助
一個產生六位隨機數的發生器多久能生成所有六位數?
這是贈券收集問題,那么期望就是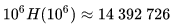 ?,H 是調和級數
?,H 是調和級數
所以我算這么多大概就能搜索到所有的可能
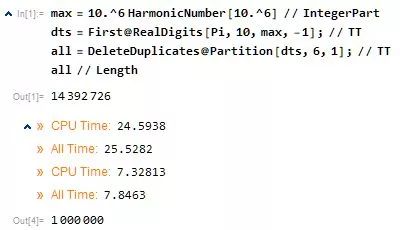
嗯,真的把十萬個個全部搜出來了
加起來也就一分鐘就不另外放下載了,自己跑一遍就行
當然你說要是沒搜到怎么辦?
這倒是有可能的,但是還是根據贈券收集原理
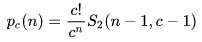
搞定的概率只有:57%
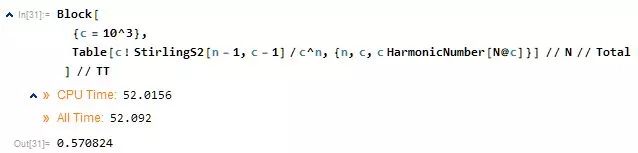
我在想這個數好眼熟....
這個數是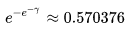
如果要以一半概率找到生日的話需要計算3.51億位,如果要找手機號要計算4606億位

查了下現在的記錄是22,459,157,718,361(224591億位), 那么找到手機號的幾率>99.9%
http://www.numberworld.org/digits/Pi/#Download
另外很多網站都提供這個服務
當然一個非超越無理數以概率1是個正規數,那么同樣適用這樣的推理
我的生日是你的生日開平方后351084058位開始8個數字我的手機是你的手機號開立方后460653489114位開始11個數字
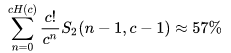
但是有個問題,斯特林數有精細結構沒法給出漸進表達式
那么考慮非均勻贈券收集問題
n,i為第$n$次選取后第$i$個樣本未被選中的情形,于是概率即為相應情形之并
然后依容斥原理展開:
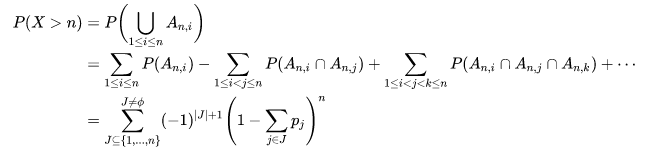
其中,$J$代表一種選法集合,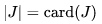 ?,即集合$J$中元素的數量。
?,即集合$J$中元素的數量。
其概率生成函數為:
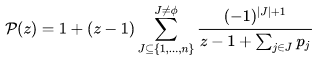
接下來對于期望而言:
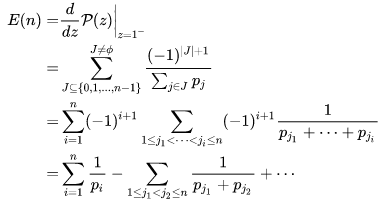
注意到
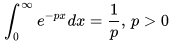
所以上式可以進一步可以寫成:
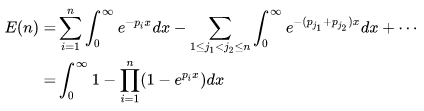
另一方面從累積分布而言:
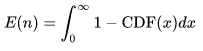
于是令
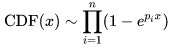
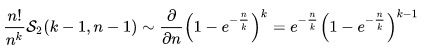
我們成功把問題轉化為連續情形:
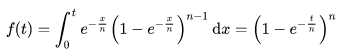
其中 n 為規模,t為計算的位數
其一階近似就是 n H(n)
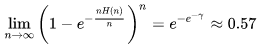
這也是臨界情況,加一個微擾全部找到的概率就是1,減一個微擾概率就是0。
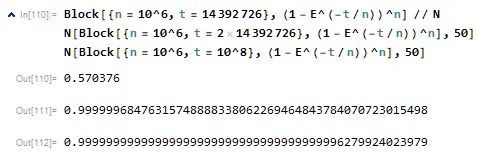
算10億位還找不全的概率幾乎為0
本文由超級數學建模編輯整理
-
數學建模
+關注
關注
0文章
49瀏覽量
14003
原文標題:π是不是真的包含了我們每個人的銀行卡密碼?
文章出處:【微信號:mcuworld,微信公眾號:嵌入式資訊精選】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
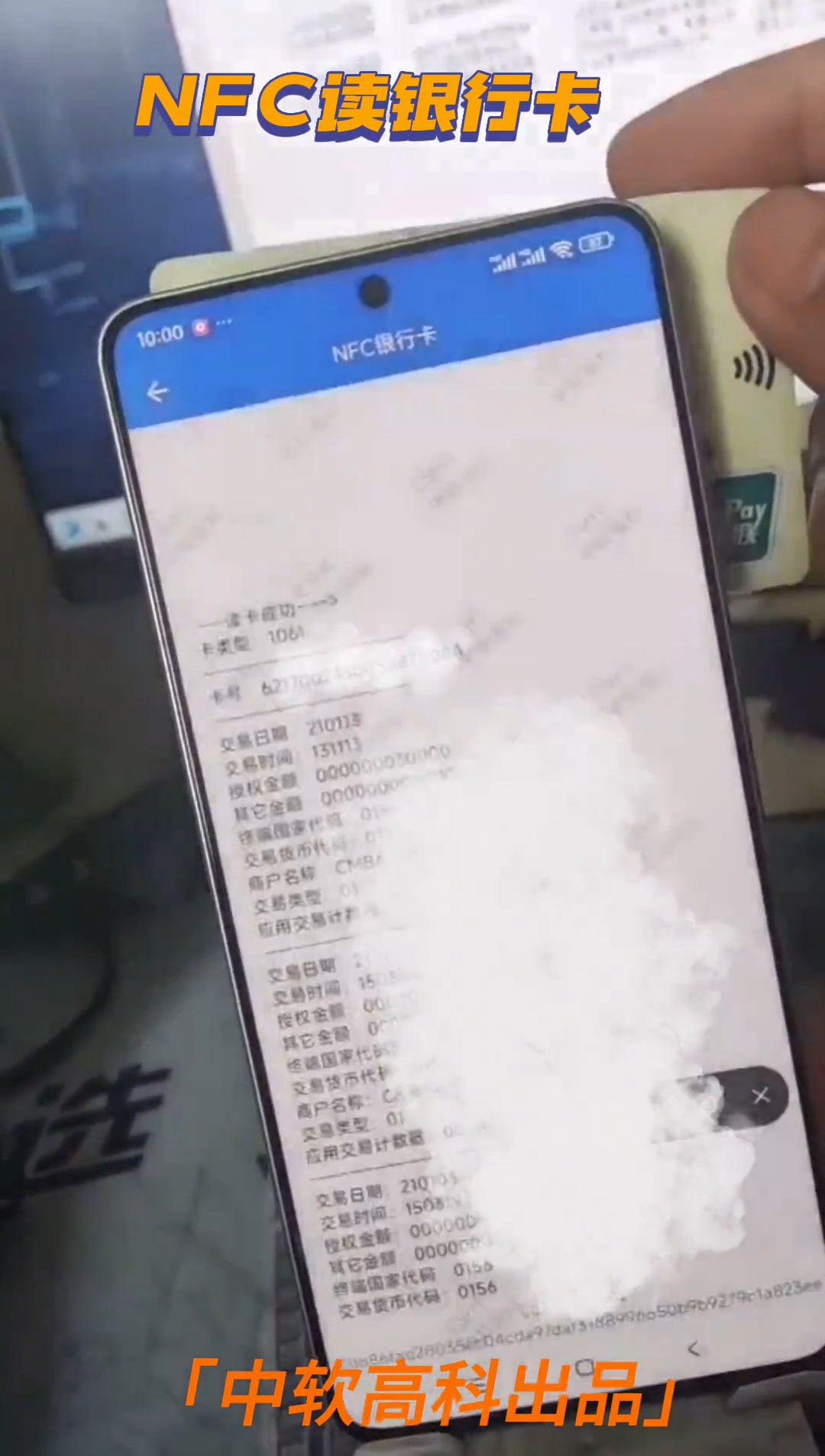
從原理到實操:SIM卡&銀行卡芯片推力測試全解

如何給軟件上密碼鎖?
Dataedo Data Catalog每個人都能養數據
科思創受邀出席2024第十屆女性領導力論壇
專家:10年后每個人需要兩臺機器人
PCM2704的ROM編程好了,竟然是亂碼,為什么?






 細思極恐:π竟然包含了我們每個人的銀行卡密碼?
細思極恐:π竟然包含了我們每個人的銀行卡密碼?












評論