現(xiàn)在,假設(shè)你已經(jīng)為某一特定問題選中了最佳的模型,并在進(jìn)一步提升其精確度上遇到了困難。在這一情形下,你將需要應(yīng)用一些更高級(jí)的機(jī)器學(xué)習(xí)技術(shù)——集成(ensemble)。
集成是一組協(xié)作貢獻(xiàn)的元素。一個(gè)熟悉的例子是合奏,組合不同的樂器創(chuàng)建動(dòng)聽的和聲。在集成中,最終的整體輸出比任何單個(gè)部分的表現(xiàn)更重要。
1. 集成
某種意義上,孔多塞陪審團(tuán)定理描述了我們之前提到的集成。該定理的內(nèi)容為,如果評(píng)審團(tuán)的每個(gè)成員做出獨(dú)立判斷,并且每個(gè)陪審員做出正確決策的概率高于0.5,那么整個(gè)評(píng)審團(tuán)做出正確的總體決策的概率隨著陪審員數(shù)量的增加而增加,并趨向于一。另一方面,如果每個(gè)陪審員判斷正確的概率小于0.5,那么整個(gè)陪審團(tuán)做出正確的總體決策的概率隨著陪審員數(shù)量的增加而減少,并趨向于零。
該定理形式化的表述為:
N為陪審員總數(shù);
m是構(gòu)成多數(shù)的最小值,即m= (N+1)/2;
p為評(píng)審員做出正確決策的概率;
μ是整個(gè)評(píng)審團(tuán)做出正確決策的概率。
則:
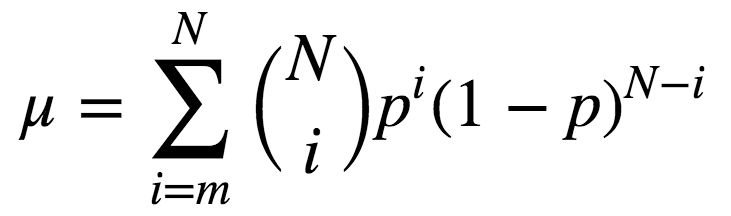
由上式可知,若p > 0.5,則μ > p。此外,若N -> ∞,則μ -> 1。
讓我們看另一個(gè)集成的例子:群體的智慧。1906年,F(xiàn)rancis Galton訪問了普利茅斯的一個(gè)農(nóng)村集市,在那里他看到一項(xiàng)競賽。800個(gè)參與者嘗試估計(jì)一頭屠宰的牛的重量。真實(shí)重量為1198磅。盡管沒人猜中這一數(shù)值,所有參與者的預(yù)測的平均值為1197磅。
機(jī)器學(xué)習(xí)領(lǐng)域采用類似的思路以降低誤差。
2. Bootstraping
Leo Breiman于1994年提出的Bagging(又稱Bootstrap aggregation,引導(dǎo)聚集)是最基本的集成技術(shù)之一。Bagging基于統(tǒng)計(jì)學(xué)中的bootstraping(自助法),該方法使得評(píng)估許多復(fù)雜模型的統(tǒng)計(jì)數(shù)據(jù)更可行。
bootstrap方法的流程如下:假設(shè)有尺寸為N的樣本X。我們可以從該樣本中有放回地隨機(jī)均勻抽取N個(gè)樣本,以創(chuàng)建一個(gè)新樣本。換句話說,我們從尺寸為N的原樣本中隨機(jī)選擇一個(gè)元素,并重復(fù)此過程N(yùn)次。選中所有元素的可能性是一樣的,因此每個(gè)元素被抽中的概率均為1/N。
假設(shè)我們從一個(gè)袋子中抽球,每次抽一個(gè)。在每一步中,將選中的球放回袋子,這樣下一次抽取是等概率的,即,從同樣數(shù)量的N個(gè)球中抽取。注意,因?yàn)槲覀儼亚蚍呕亓耍聵颖局锌赡苡兄貜?fù)的球。讓我們把這個(gè)新樣本稱為X1。
重復(fù)這一過程M次,我們創(chuàng)建M個(gè)bootstrap樣本X1,……,XM。最后,我們有了足夠數(shù)量的樣本,可以計(jì)算原始分布的多種統(tǒng)計(jì)數(shù)據(jù)。
讓我們看一個(gè)例子,我們將使用之前的telecom_churn數(shù)據(jù)集。我們?cè)?jīng)討論過這一數(shù)據(jù)集的特征重要性,其中最重要的特征之一是呼叫客服次數(shù)。讓我們可視化這一數(shù)據(jù),看看該特征的分布。
import pandas as pd
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = 10, 6
import seaborn as sns
%matplotlib inline
telecom_data = pd.read_csv('../../data/telecom_churn.csv')
fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == False]['Customer service calls'],
label = 'Loyal')
fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == True]['Customer service calls'],
label = 'Churn')
fig.set(xlabel='Number of calls', ylabel='Density')
plt.show()
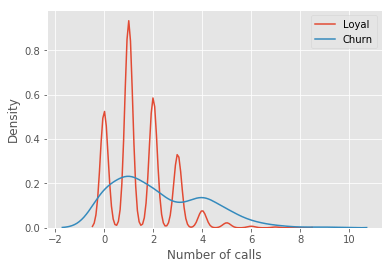
如你所見,相比那些逐漸離網(wǎng)的客戶,忠實(shí)客戶呼叫客服的次數(shù)更少。估計(jì)每組客戶的平均呼叫客服數(shù)可能是個(gè)好主意。由于我們的數(shù)據(jù)集很小,如果直接計(jì)算原樣本的均值,我們得到的估計(jì)可能不好。因此我們將應(yīng)用bootstrap方法。讓我們基于原樣本生成1000新bootstrap樣本,然后計(jì)算均值的區(qū)間估計(jì)。
import numpy as np
def get_bootstrap_samples(data, n_samples):
"""使用bootstrap方法生成bootstrap樣本。"""
indices = np.random.randint(0, len(data), (n_samples, len(data)))
samples = data[indices]
return samples
def stat_intervals(stat, alpha):
"""生成區(qū)間估計(jì)。"""
boundaries = np.percentile(stat, [100 * alpha / 2., 100 * (1 - alpha / 2.)])
return boundaries
分割數(shù)據(jù)集,分組為忠實(shí)客戶和離網(wǎng)客戶:
loyal_calls = telecom_data[telecom_data['Churn']
== False]['Customer service calls'].values
churn_calls= telecom_data[telecom_data['Churn']
== True]['Customer service calls'].values
固定隨機(jī)數(shù)種子,以得到可重現(xiàn)的結(jié)果。
np.random.seed(0)
使用bootstrap生成樣本,計(jì)算各自的均值。
loyal_mean_scores = [np.mean(sample)
for sample in get_bootstrap_samples(loyal_calls, 1000)]
churn_mean_scores = [np.mean(sample)
for sample in get_bootstrap_samples(churn_calls, 1000)]
打印區(qū)間估計(jì)值。
print("忠實(shí)客戶呼叫客服數(shù): 均值區(qū)間",
stat_intervals(loyal_mean_scores, 0.05))
print("離網(wǎng)客戶呼叫客服數(shù):均值區(qū)間",
stat_intervals(churn_mean_scores, 0.05))
結(jié)果:
忠實(shí)客戶呼叫客服數(shù): 均值區(qū)間 [1.40771931.49473684]
離網(wǎng)客戶呼叫客服數(shù):均值區(qū)間 [2.06211182.39761905]
因此,我們看到,有95%的概率,忠實(shí)客戶平均呼叫客服的次數(shù)在1.4到1.49之間,而離網(wǎng)客戶平均呼叫客服的次數(shù)在2.06到2.40之間。另外,注意忠實(shí)客戶的區(qū)間更窄,這是合理的,因?yàn)椋啾榷啻魏艚锌头罱K受夠了轉(zhuǎn)換運(yùn)營商的離網(wǎng)客戶,忠實(shí)客戶呼叫客服的次數(shù)更少(0、1、2)。
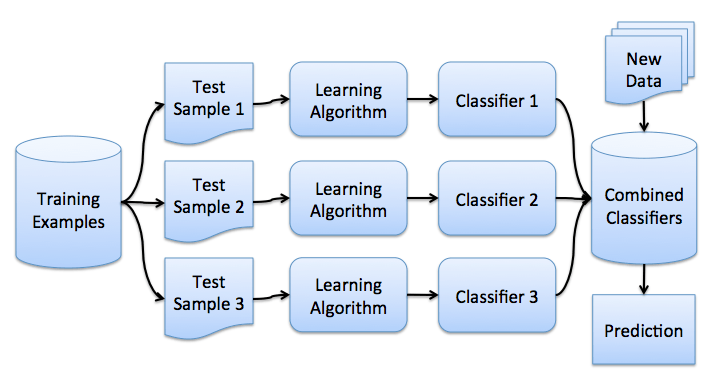
3. Bagging
理解了bootstrap概念之后,我們來介紹bagging。
假設(shè)我們有一個(gè)訓(xùn)練集X。我們使用bootstrap生成樣本X1, ..., XM。現(xiàn)在,我們?cè)诿總€(gè)bootstrap樣本上分別訓(xùn)練分類器ai(x)。最終分類器將對(duì)所有這些單獨(dú)的分類器的輸出取均值。在分類情形下,該技術(shù)對(duì)應(yīng)投票(voting):
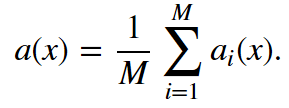
在回歸問題中,通過對(duì)回歸結(jié)果取均值,bagging將均方誤差降至1/M(M為回歸器數(shù)量)。
回顧一下上一課的內(nèi)容,模型的預(yù)測誤差有三部分構(gòu)成:
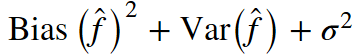
bagging通過在不同數(shù)據(jù)集上訓(xùn)練模型降低分類器的方差。換句話說,bagging可以預(yù)防過擬合。bagging的有效性來自不同訓(xùn)練數(shù)據(jù)集上單獨(dú)模型的不同,它們的誤差在投票過程中相互抵消。此外,某些bootstrap訓(xùn)練樣本很可能略去離散值。
讓我們看下bagging的實(shí)際效果,并與決策樹比較下。我們將使用sklearn文檔中的一個(gè)例子。
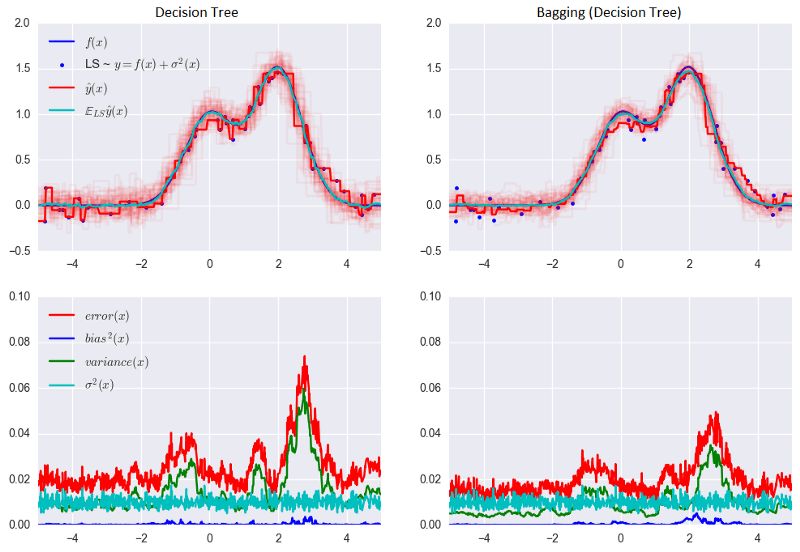
從上圖可以看到,就bagging而言,誤差中的方差顯著降低了。
上面的例子不太可能在實(shí)際工作中出現(xiàn)。因?yàn)槲覀冏隽艘粋€(gè)很強(qiáng)的假定,單獨(dú)誤差是不相關(guān)的。對(duì)現(xiàn)實(shí)世界的應(yīng)用而言,這經(jīng)常是過于樂觀了。當(dāng)這個(gè)假定為假時(shí),誤差的下降不會(huì)那么顯著。在后續(xù)課程中,我們將討論一些更復(fù)雜的集成方法,能夠在現(xiàn)實(shí)世界的問題中做出更精確的預(yù)測。
4. 袋外誤差
隨機(jī)森林不需要使用交叉驗(yàn)證或留置樣本,因?yàn)樵谶@一集成技術(shù)內(nèi)置了誤差估計(jì)。
隨機(jī)森林中的決策樹基于原始數(shù)據(jù)集中不同的bootstrap樣本構(gòu)建。對(duì)第K棵樹而言,其特定bootstrap樣本大約留置了37%的輸入。
這很容易證明。設(shè)數(shù)據(jù)集中有l(wèi)個(gè)樣本。在每一步,每個(gè)數(shù)據(jù)點(diǎn)最終出現(xiàn)在有放回的bootstrap樣本中的概率均為1/l。bootstrap樣本最終不包含特定數(shù)據(jù)集元素的概率(即,該元素在l次抽取中都沒抽中)等于(1 - 1/l)l。當(dāng)l -> +∞時(shí),這一概率等于1/e。因此,選中某一特定樣本的概率為1 - 1/e,約等于63%。
下面讓我們可視化袋外誤差(Out-of-BagError,OOBE)估計(jì)是如何工作的:
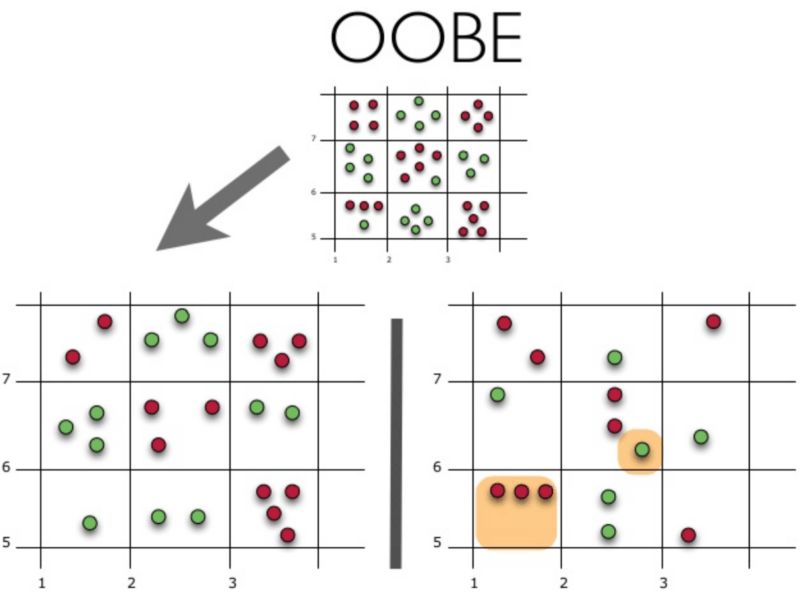
示意圖上方為原始數(shù)據(jù)集。我們將其分為訓(xùn)練集(左)和測試集(右)。在測試集上,我們繪制一副網(wǎng)格,完美地實(shí)施了分類。現(xiàn)在,我們應(yīng)用同一副網(wǎng)格于測試集,以估計(jì)分類的正確率。我們可以看到,分類器在4個(gè)未曾在訓(xùn)練中使用的數(shù)據(jù)點(diǎn)上給出了錯(cuò)誤的答案。而測試集中共有15個(gè)數(shù)據(jù)點(diǎn),這15個(gè)數(shù)據(jù)點(diǎn)未在訓(xùn)練中使用。因此,我們的分類器的精確度為11/15 * 100% = 73.33%.
總結(jié)一下,每個(gè)基礎(chǔ)算法在約63%的原始樣本上訓(xùn)練。該算法可以在剩下的約37%的樣本上驗(yàn)證。袋外估計(jì)不過是基礎(chǔ)算法在訓(xùn)練過程中留置出來的約37%的輸入上的平均估計(jì)。
5. 隨機(jī)森林
Leo Breiman不僅將bootstrap應(yīng)用于統(tǒng)計(jì),同時(shí)也將其應(yīng)用于機(jī)器學(xué)習(xí)。他和Adel Cutler擴(kuò)展并改進(jìn)了Tin Kam Ho提出的的隨機(jī)森林算法。他們組合使用CART、bagging、隨機(jī)子空間方法構(gòu)建無關(guān)樹。
在bagging中,決策樹是一個(gè)基礎(chǔ)分類器的好選項(xiàng),因?yàn)樗鼈兿喈?dāng)復(fù)雜,并能在任何樣本上達(dá)到零分類誤差。隨機(jī)子空間方法降低樹的相關(guān)性,從而避免過擬合。基于bagging,基礎(chǔ)算法在不同的原始特征集的隨機(jī)子集上訓(xùn)練。
以下算法使用隨機(jī)子空間方法構(gòu)建模型集成:
設(shè)樣本數(shù)等于n,特征維度數(shù)等于d。
選擇集成中單個(gè)模型的數(shù)目M。
對(duì)于每個(gè)模型m,選擇特征數(shù)dm < d。所有模型使用相同的dm值。
對(duì)每個(gè)模型m,通過在整個(gè)d特征集合上隨機(jī)選擇dm個(gè)特征創(chuàng)建一個(gè)訓(xùn)練集。
訓(xùn)練每個(gè)模型。
通過組合M中的所有模型的結(jié)果,應(yīng)用所得集成模型于新輸入。可以使用大多數(shù)投票(majority voting)或后驗(yàn)概率加總(aggregation of the posterior probabilities)。
5.1 算法
構(gòu)建N樹隨機(jī)森林的算法如下:
對(duì)每個(gè)k = 1, ..., N:
生成bootstrap樣本Xk。
在樣本Xk上創(chuàng)建一棵決策樹bk:
根據(jù)給定的標(biāo)準(zhǔn)選擇最佳的特征維度。根據(jù)該特征分割樣本以創(chuàng)建樹的新層次。重復(fù)這一流程,直到竭盡樣本。
創(chuàng)建樹,直到任何葉節(jié)點(diǎn)包含不超過nmin個(gè)實(shí)例,或者達(dá)到特定深度。
對(duì)每個(gè)分割,我們首先從d個(gè)原始特征中隨機(jī)選擇m個(gè)特征,接著只在該子集上搜索最佳分割。
最終分類器定義為:
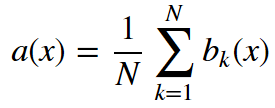
分類問題使用多數(shù)投票,回歸問題使用均值。
在分類問題中,建議將m設(shè)定為d的平方根,取nmin= 1。回歸問題中,一般取m = d/3,nmin= 5。
你可以將隨機(jī)森林看成決策樹bagging加上一個(gè)改動(dòng),在每個(gè)分割處選擇一個(gè)隨機(jī)特征子空間。
5.2 與決策樹和bagging的比較
導(dǎo)入所需包,配置環(huán)境:
import warnings
import numpy as np
warnings.filterwarnings('ignore')
%matplotlib inline
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = 10, 6
import seaborn as sns
from sklearn.ensemble importRandomForestRegressor, RandomForestClassifier
from sklearn.ensemble importBaggingClassifier, BaggingRegressor
from sklearn.tree importDecisionTreeRegressor, DecisionTreeClassifier
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
n_train = 150
n_test = 1000
noise = 0.1
生成數(shù)據(jù):
def f(x):
x = x.ravel()
return np.exp(-x ** 2) + 1.5 * np.exp(-(x - 2) ** 2)
def generate(n_samples, noise):
X = np.random.rand(n_samples) * 10 - 5
X = np.sort(X).ravel()
y = np.exp(-X ** 2) + 1.5 * np.exp(-(X - 2) ** 2)\
+ np.random.normal(0.0, noise, n_samples)
X = X.reshape((n_samples, 1))
return X, y
X_train, y_train = generate(n_samples=n_train, noise=noise)
X_test, y_test = generate(n_samples=n_test, noise=noise)
單棵決策樹回歸:
dtree = DecisionTreeRegressor().fit(X_train, y_train)
d_predict = dtree.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, d_predict, "g", lw=2)
plt.xlim([-5, 5])
plt.title("Decision tree, MSE = %.2f"
% np.sum((y_test - d_predict) ** 2))
決策樹回歸bagging:
bdt = BaggingRegressor(DecisionTreeRegressor()).fit(X_train, y_train)
bdt_predict = bdt.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, bdt_predict, "y", lw=2)
plt.xlim([-5, 5])
plt.title("Bagging for decision trees, MSE = %.2f" % np.sum((y_test - bdt_predict) ** 2));
隨機(jī)森林:
rf = RandomForestRegressor(n_estimators=10).fit(X_train, y_train)
rf_predict = rf.predict(X_test)
plt.figure(figsize=(10, 6))
plt.plot(X_test, f(X_test), "b")
plt.scatter(X_train, y_train, c="b", s=20)
plt.plot(X_test, rf_predict, "r", lw=2)
plt.xlim([-5, 5])
plt.title("Random forest, MSE = %.2f" % np.sum((y_test - rf_predict) ** 2));
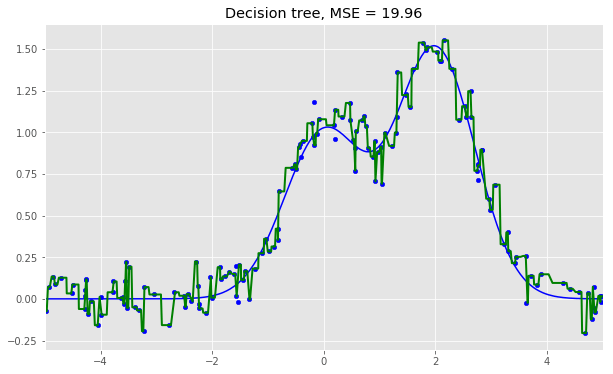
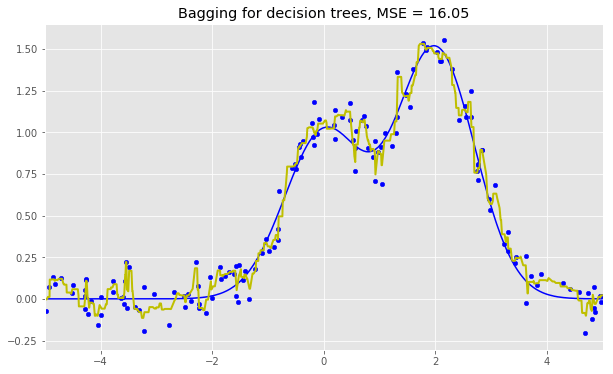
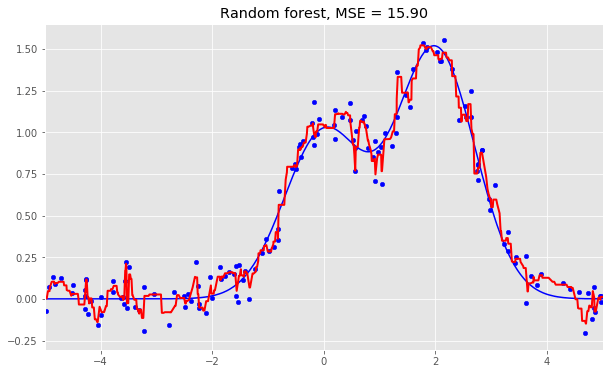
從上面的圖像和MSE值可以看到,10樹隨機(jī)森林比單棵決策樹和10樹bagging的表現(xiàn)要好。(譯者注:實(shí)際上,在這個(gè)例子中,隨機(jī)森林的表現(xiàn)并不穩(wěn)定,多次運(yùn)行的結(jié)果是,隨機(jī)森林和bagging互有勝負(fù)。)隨機(jī)森林和bagging的主要差別在于,在隨機(jī)森林中,分割的最佳特征是從一個(gè)隨機(jī)特征子空間中選取的,而在bagging中,分割時(shí)將考慮所有特征。
接下來,我們將查看隨機(jī)森林和bagging在分類問題上的表現(xiàn):
np.random.seed(42)
X, y = make_circles(n_samples=500, factor=0.1, noise=0.35, random_state=42)
X_train_circles, X_test_circles, y_train_circles, y_test_circles = train_test_split(X, y, test_size=0.2)
dtree = DecisionTreeClassifier(random_state=42)
dtree.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = dtree.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
plt.title("Decision tree")
plt.show()
b_dtree = BaggingClassifier(DecisionTreeClassifier(),n_estimators=300, random_state=42)
b_dtree.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = b_dtree.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
plt.title("Bagging (decision trees)")
plt.show()
rf = RandomForestClassifier(n_estimators=300, random_state=42)
rf.fit(X_train_circles, y_train_circles)
x_range = np.linspace(X.min(), X.max(), 100)
xx1, xx2 = np.meshgrid(x_range, x_range)
y_hat = rf.predict(np.c_[xx1.ravel(), xx2.ravel()])
y_hat = y_hat.reshape(xx1.shape)
plt.contourf(xx1, xx2, y_hat, alpha=0.2)
plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn')
plt.title("Random forest")
plt.show()
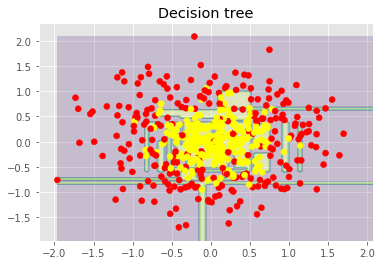
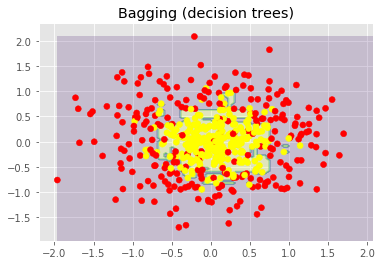
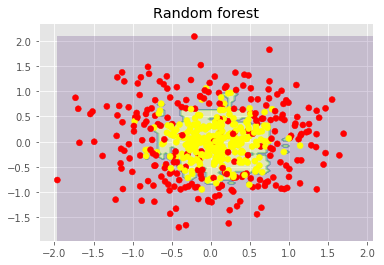
上圖顯示了決策樹判定的邊界相當(dāng)凹凸不平,有大量銳角,這暗示了過擬合,概括性差。相反,隨機(jī)森林和bagging的邊界相當(dāng)平滑,沒有明顯的過擬合的跡象。
現(xiàn)在,讓我們查看一些有助于提高模型精確度的參數(shù)。
5.3 參數(shù)
scikit-learn庫提供了BaggingRegressor和BaggingClassifier。
下面是創(chuàng)建新模型時(shí)需要注意的一些參數(shù):
n_estimators是森林中樹的數(shù)量;
criterion是衡量分割質(zhì)量的函數(shù);
max_features是查找最佳分割時(shí)考慮的特征數(shù);
min_samples_leaf是葉節(jié)點(diǎn)的最小樣本數(shù);
max_depth是樹的最大深度。
在真實(shí)問題中練習(xí)隨機(jī)森林
我們將使用之前的離網(wǎng)預(yù)測作為例子。這是一個(gè)分類問題,我們將使用精確度評(píng)估模型。
import pandas as pd
from sklearn.model_selection import cross_val_score, StratifiedKFold, GridSearchCV
from sklearn.metrics import accuracy_score
df = pd.read_csv("../../data/telecom_churn.csv")
首先,讓我們創(chuàng)建一個(gè)簡單的分類器作為基線。出于簡單性,我們將只使用數(shù)值特征。
cols = []
for i in df.columns:
if (df[i].dtype == "float64") or (df[i].dtype == 'int64'):
cols.append(i)
分離數(shù)據(jù)集為輸入和目標(biāo):
X, y = df[cols].copy(), np.asarray(df["Churn"],dtype='int8')
為驗(yàn)證過程進(jìn)行分層分割:
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
基于默認(rèn)參數(shù)初始化分類器:
rfc = RandomForestClassifier(random_state=42, n_jobs=-1, oob_score=True)
在訓(xùn)練集上進(jìn)行訓(xùn)練:
results = cross_val_score(rfc, X, y, cv=skf)
在測試集上評(píng)估精確度:
print("交叉驗(yàn)證精確度評(píng)分: {:.2f}%".format(results.mean()*100))
結(jié)果:
交叉驗(yàn)證精確度評(píng)分:91.48%
現(xiàn)在,讓我們嘗試改進(jìn)結(jié)果,同時(shí)查看下修改基本參數(shù)時(shí)學(xué)習(xí)曲線的表現(xiàn)。
讓我們從樹的數(shù)量開始:
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
創(chuàng)建列表儲(chǔ)存訓(xùn)練集和測試集上的精確度數(shù)值:
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
進(jìn)行網(wǎng)格搜索:
trees_grid = [5, 10, 15, 20, 30, 50, 75, 100]
在訓(xùn)練集上訓(xùn)練:
for ntrees in trees_grid:
rfc = RandomForestClassifier(n_estimators=ntrees, random_state=42, n_jobs=-1, oob_score=True)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
打印結(jié)果:
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("交叉驗(yàn)證最佳精確度為 {:.2f}% 在 {} 樹時(shí)達(dá)到".format(max(test_acc.mean(axis=1))*100,
trees_grid[np.argmax(test_acc.mean(axis=1))]))
結(jié)果:
交叉驗(yàn)證最佳精確度為 92.44% 在 50 樹時(shí)達(dá)到
接下來,我們繪制相應(yīng)的學(xué)習(xí)曲線:
plt.style.use('ggplot')
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(trees_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(trees_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(trees_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(trees_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("N_estimators");
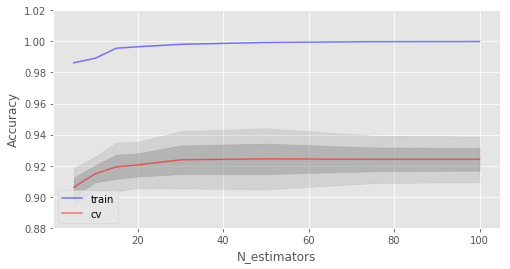
如你所見,當(dāng)達(dá)到特定數(shù)量時(shí),測試集上的精確度非常接近漸近線。
上圖同時(shí)顯示了我們?cè)谟?xùn)練集上達(dá)到了100%精確度,這意味著我們過擬合了。為了避免過擬合,我們需要給模型加上正則化參數(shù)。
下面我們將樹的數(shù)目固定為100,然后看看不同的max_depth效果如何:
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
max_depth_grid = [3, 5, 7, 9, 11, 13, 15, 17, 20, 22, 24]
for max_depth in max_depth_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1, oob_score=True, max_depth=max_depth)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("交叉驗(yàn)證最佳精確度為 {:.2f}% 當(dāng) max_depth 為 {} 時(shí)達(dá)到".format(max(test_acc.mean(axis=1))*100,
max_depth_grid[np.argmax(test_acc.mean(axis=1))]))
結(jié)果:
交叉驗(yàn)證最佳精確度為 92.68% 當(dāng) max_depth 為 17 時(shí)達(dá)到
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(max_depth_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(max_depth_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("Max_depth");
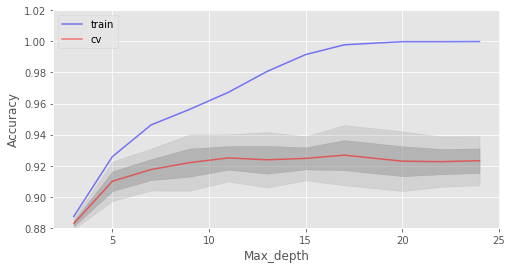
max_depth在我們的模型中起到了正則化的作用,模型不像之前過擬合得那么嚴(yán)重了。模型精確度略有提升。
另一個(gè)值得調(diào)整的重要參數(shù)是min_samples_leaf,它也能起到正則化作用。
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
min_samples_leaf_grid = [1, 3, 5, 7, 9, 11, 13, 15, 17, 20, 22, 24]
for min_samples_leaf in min_samples_leaf_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1,
oob_score=True, min_samples_leaf=min_samples_leaf)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("交叉驗(yàn)證最佳精確度為 {:.2f}% 當(dāng) min_samples_leaf 為 {} 時(shí)達(dá)到".format(max(test_acc.mean(axis=1))*100,
min_samples_leaf_grid[np.argmax(test_acc.mean(axis=1))]))
結(jié)果:
交叉驗(yàn)證最佳精確度為 92.41% 當(dāng) min_samples_leaf 為 3 時(shí)達(dá)到
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(min_samples_leaf_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(min_samples_leaf_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("Min_samples_leaf");
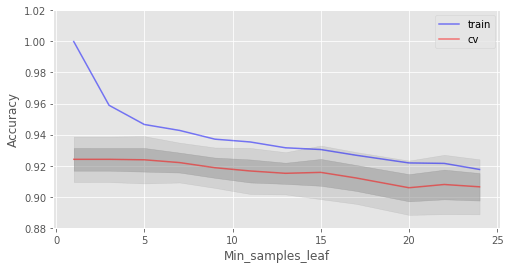
在這一情形下,我們沒在驗(yàn)證集上看到精確度提升,但在驗(yàn)證集上精確度保持92%以上的同時(shí),降低了2%的過擬合。
考慮max_features這一參數(shù)。在分類問題中,所有特征數(shù)的平方根是默認(rèn)選擇。讓我們看下4個(gè)特征是否是這個(gè)例子中的最佳選擇:
train_acc = []
test_acc = []
temp_train_acc = []
temp_test_acc = []
max_features_grid = [2, 4, 6, 8, 10, 12, 14, 16]
for max_features in max_features_grid:
rfc = RandomForestClassifier(n_estimators=100, random_state=42, n_jobs=-1,
oob_score=True, max_features=max_features)
temp_train_acc = []
temp_test_acc = []
for train_index, test_index in skf.split(X, y):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y[train_index], y[test_index]
rfc.fit(X_train, y_train)
temp_train_acc.append(rfc.score(X_train, y_train))
temp_test_acc.append(rfc.score(X_test, y_test))
train_acc.append(temp_train_acc)
test_acc.append(temp_test_acc)
train_acc, test_acc = np.asarray(train_acc), np.asarray(test_acc)
print("交叉驗(yàn)證最佳精確度為 {:.2f}% 當(dāng) max_features 為 {} 時(shí)達(dá)到".format(max(test_acc.mean(axis=1))*100,
max_features_grid[np.argmax(test_acc.mean(axis=1))]))
結(jié)果:
交叉驗(yàn)證最佳精確度為 92.59% 當(dāng) max_features 為 10 時(shí)達(dá)到
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(max_features_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train')
ax.plot(max_features_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv')
ax.fill_between(max_features_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4)
ax.fill_between(max_features_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2)
ax.legend(loc='best')
ax.set_ylim([0.88,1.02])
ax.set_ylabel("Accuracy")
ax.set_xlabel("Max_features");
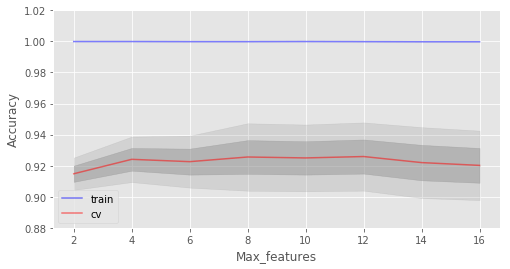
在我們的例子中,最佳特征數(shù)是10。
我們已經(jīng)查看了基本參數(shù)的不同值的學(xué)習(xí)曲線。下面讓我們使用GridSearch查找最佳參數(shù):
parameters = {'max_features': [4, 7, 10, 13], 'min_samples_leaf': [1, 3, 5, 7], 'max_depth': [5,10,15,20]}
rfc = RandomForestClassifier(n_estimators=100, random_state=42,
n_jobs=-1, oob_score=True)
gcv = GridSearchCV(rfc, parameters, n_jobs=-1, cv=skf, verbose=1)
gcv.fit(X, y)
gcv.best_estimator_, gcv.best_score_
返回:
(RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=10, max_features=10, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=-1,
oob_score=True, random_state=42, verbose=0, warm_start=False),
0.9270927092709271)
隨機(jī)森林最重要的一點(diǎn)是它的精確度不會(huì)隨著樹的增加而下降,所以樹的數(shù)量不像max_depth和min_samples_leaf那樣錯(cuò)綜復(fù)雜。這意味著你可以使用,比如說,10棵樹調(diào)整超參數(shù),接著增加樹的數(shù)量至500,放心,精確度只會(huì)更好。
5.4 方差和去相關(guān)
隨機(jī)森林的方差可以用下式表達(dá):
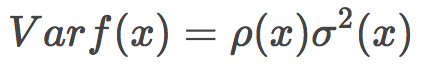
其中
p(x)為任何兩棵樹之間的樣本相關(guān)性;
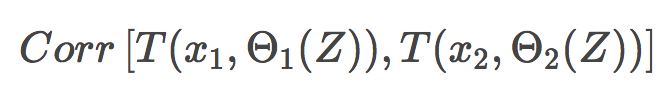
Θ1(Z)和Θ2(Z)為樣本Z上隨機(jī)選擇的元素上隨機(jī)選擇的一對(duì)樹;
T(x, Θi(Z))為第i個(gè)樹分類器在輸入向量x上的輸出;
σ2(x)為任何隨機(jī)選擇的樹上的樣本方差:
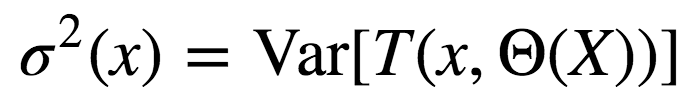
很容易將p(x)誤認(rèn)為給定的隨機(jī)森林中訓(xùn)練好的樹的平均相關(guān)性(將樹視為N維向量)。其實(shí)并非如此。
事實(shí)上,這一條件相關(guān)性并不和平均過程直接相關(guān),p(x)的自變量x提醒了我們這一差別。p(x)是一對(duì)隨機(jī)樹在輸入x上的估計(jì)的理論相關(guān)性。它的值源自重復(fù)取樣訓(xùn)練集以及之后隨機(jī)選擇的決策樹對(duì)。用統(tǒng)計(jì)學(xué)術(shù)語來說,這是由Z和Θ取樣分布導(dǎo)致的相關(guān)性。
任何一對(duì)樹的條件相關(guān)性等于0,因?yàn)閎ootstrap和特征選取是獨(dú)立同分布。
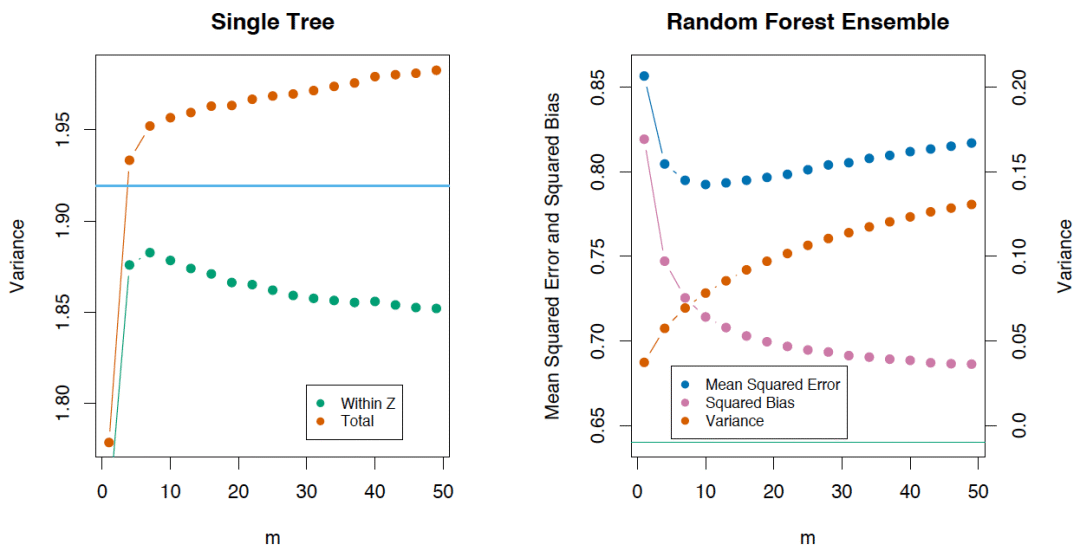
如果我們考慮單棵樹的方差,它幾乎不受分割參數(shù)的影響(m)。但這一參數(shù)在集成中是關(guān)鍵。另外,單棵決策樹的方差要比集成高很多。The Elements of Statistical Learning一書中有一個(gè)很好的例子:
5.5 偏差
隨機(jī)森林、bagging的偏差和單棵決策樹一樣:
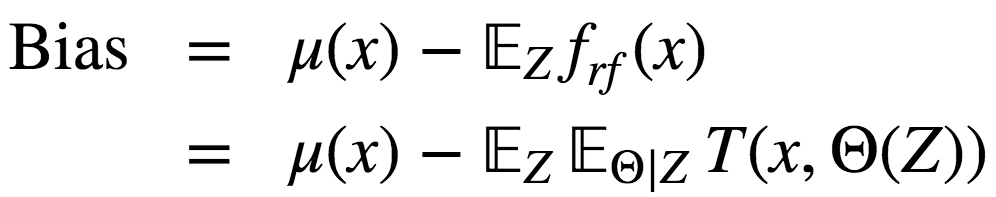
從絕對(duì)值上說,偏差通常比單棵樹要大,因?yàn)殡S機(jī)過程和樣本空間縮減在模型上施加了它們各自的限制。因此,bagging和隨機(jī)森林在預(yù)測精確度上的提升單純?cè)醋苑讲罱档汀?/p>
5.6 極端隨機(jī)樹
極端隨機(jī)樹(Extremely Randomized Trees)在節(jié)點(diǎn)分岔時(shí)應(yīng)用了更多隨機(jī)性。和隨機(jī)森林一樣,極端隨機(jī)樹使用一個(gè)隨機(jī)特征子空間。然而,極端隨機(jī)數(shù)并不搜尋最佳閾值,相反,為每個(gè)可能的特征隨機(jī)生成一個(gè)閾值,然后根據(jù)其中最佳隨機(jī)生成閾值對(duì)應(yīng)的特征來分割節(jié)點(diǎn)。這通常是用少量偏差的增加交換方差的略微下降。
scikit-learn庫實(shí)現(xiàn)了[ ExtraTreesClassifier]和ExtraTreesRegressor。
如果你使用隨機(jī)森林或梯度提升遇到了嚴(yán)重的過擬合,可以試試極端隨機(jī)樹。
5.7 隨機(jī)森林和k近鄰的相似性
隨機(jī)森林和最近鄰技術(shù)有相似之處。隨機(jī)森林預(yù)測基于訓(xùn)練集中相似樣本的標(biāo)簽。這些樣本越常出現(xiàn)在同一葉節(jié)點(diǎn),它們的相似度就越高。下面我們將證明這一點(diǎn)。
讓我們考慮一個(gè)二次損失函數(shù)的回歸問題。設(shè)Tn(x)為輸入x在隨機(jī)森林中第n棵樹的葉節(jié)點(diǎn)數(shù)。算法對(duì)輸入向量x的響應(yīng)等于所有落入葉節(jié)點(diǎn)Tn(x)的訓(xùn)練樣本的平均響應(yīng)。
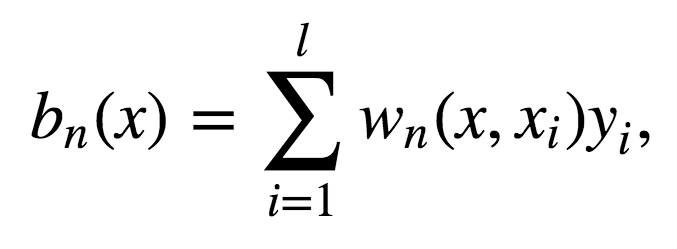
其中
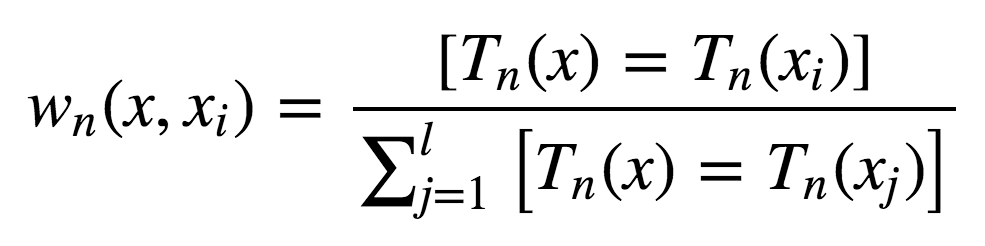
故響應(yīng)的構(gòu)成為:
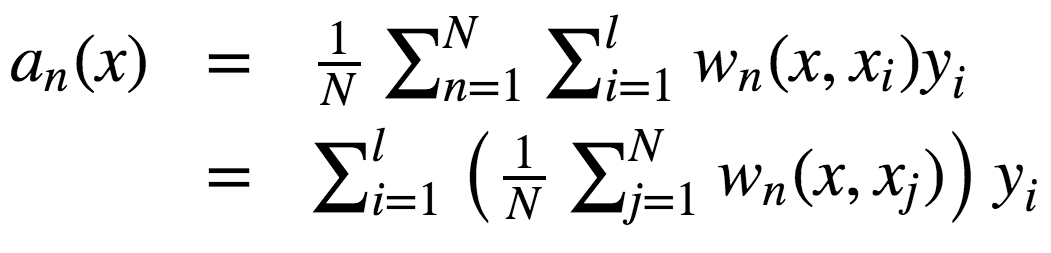
如你所見,隨機(jī)森林的響應(yīng)為所有訓(xùn)練樣本響應(yīng)的加權(quán)和。
同時(shí),值得注意的是,實(shí)例x最終出現(xiàn)的葉節(jié)點(diǎn)數(shù)Tn(x),本身是一個(gè)有價(jià)值的特征。例如,下面的方法效果不錯(cuò):
基于隨機(jī)森林或梯度提升技術(shù)在樣本上訓(xùn)練較小數(shù)目的決策樹的復(fù)合模型
將類別特征T1(x),...,Tn(x)加入樣本
這些新特征是非線性空間分割的結(jié)果,它們提供了關(guān)于樣本之間的相似性的信息。The Elements of Statistical Learning一書中有一個(gè)很好的說明樣例,演示了隨機(jī)森林和k-近鄰技術(shù)的相似性:
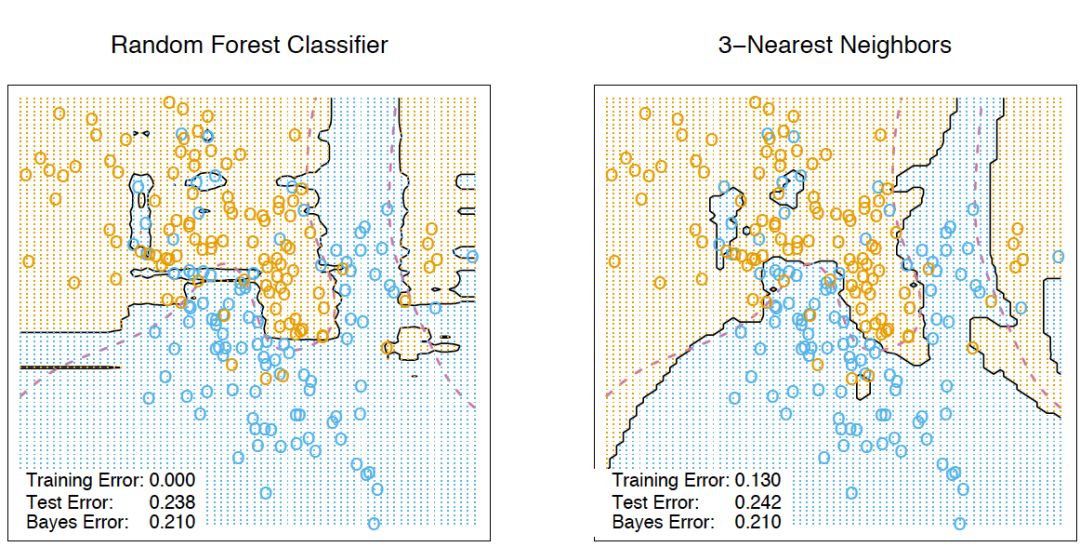
5.8 轉(zhuǎn)換數(shù)據(jù)集為高維表示
隨機(jī)森林主要用于監(jiān)督學(xué)習(xí),不過也可以在無監(jiān)督設(shè)定下應(yīng)用。
使用scikit-learn的RandomTreesEmbedding方法,我們可以將數(shù)據(jù)集轉(zhuǎn)換為高維的稀疏表示。我們首先創(chuàng)建一些極端隨機(jī)樹,接著使用包含樣本的葉節(jié)點(diǎn)索引作為新特征。
例如,如果第一個(gè)葉節(jié)點(diǎn)包含輸入,我們分配1為特征值,否則,分配0. 這稱為二進(jìn)制編碼(binary coding)。我們可以通過增減樹的數(shù)目和深度控制特征數(shù)量和稀疏性。由于鄰居的數(shù)據(jù)點(diǎn)傾向于落入同一葉節(jié)點(diǎn),這一轉(zhuǎn)換提供了對(duì)數(shù)據(jù)點(diǎn)的密度的一個(gè)隱式的非參數(shù)估計(jì)。
5.9 隨機(jī)森林的優(yōu)勢和劣勢
優(yōu)勢:
高預(yù)測精確度;在大多數(shù)問題上表現(xiàn)優(yōu)于線性算法;精確度與boosting相當(dāng);
多虧了隨機(jī)取樣,對(duì)離散值的魯棒性較好;
隨機(jī)子空間選取導(dǎo)致對(duì)特征縮放及其他單調(diào)轉(zhuǎn)換不敏感;
不需要精細(xì)的參數(shù)調(diào)整,開箱即用。取決于問題設(shè)定和數(shù)據(jù),調(diào)整參數(shù)可能取得0.5%到3%的精確度提升;
在具有大量特征和分類的數(shù)據(jù)集上很高效;
既可處理連續(xù)值,也可處理離散值;
罕見過擬合。在實(shí)踐中,增加樹的數(shù)量幾乎總是能提升總體表現(xiàn)。不過,當(dāng)達(dá)到特定數(shù)量后,學(xué)習(xí)曲線非常接近漸近線;
有成熟方法用于估計(jì)特征重要性;
能夠很好地處理數(shù)據(jù)缺失,即使當(dāng)很大一部分?jǐn)?shù)據(jù)缺失時(shí),仍能保持較好的精確度;
支持整個(gè)數(shù)據(jù)集及單棵樹樣本上的加權(quán)分類;
決策樹底層使用的實(shí)例親近性計(jì)算可以在后續(xù)用于聚類、檢測離散值、感興趣數(shù)據(jù)表示;
以上功能和性質(zhì)可以擴(kuò)展到未標(biāo)注數(shù)據(jù),以支持無監(jiān)督聚類,數(shù)據(jù)可視化和離散值檢測;
易于并行化,伸縮性強(qiáng)。
劣勢:
相比單棵決策樹,隨機(jī)森林的輸出更難解釋。
特征重要性估計(jì)沒有形式化的p值。
在稀疏數(shù)據(jù)情形(比如,文本輸入、詞袋)下,表現(xiàn)不如線性模型好。
和線性回歸不同,隨機(jī)森林無法外推。不過,這也可以看成優(yōu)勢,因?yàn)殡x散值不會(huì)在隨機(jī)森林中導(dǎo)致極端值。
在某些問題上容易過擬合,特別是處理高噪聲數(shù)據(jù)。
處理數(shù)量級(jí)不同的類別數(shù)據(jù)時(shí),隨機(jī)森林偏重?cái)?shù)量級(jí)較高的變量,因?yàn)檫@能提高更多精確度;
如果數(shù)據(jù)集包含對(duì)預(yù)測分類重要度相似的相關(guān)特征分組,那么隨機(jī)森林將偏重較小的分組;
所得模型較大,需要大量RAM。
6. 特征重要性
我們常常需要給出算法輸出某個(gè)特定答案的原因。或者,在不能完全理解算法的情況下,我們至少想要找出哪個(gè)輸入特征對(duì)結(jié)果的貢獻(xiàn)最大。基于隨機(jī)森林,我們可以相當(dāng)容易地獲取這類信息。
方法精要
下圖很直觀地呈現(xiàn)了,在我們的信用評(píng)分問題中,年齡比收入更重要。基于信息增益這一概念,我們可以形式化地解釋這一點(diǎn)。
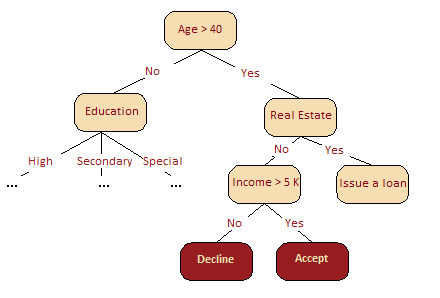
在隨機(jī)森林中,某一特征在所有樹中離樹根的平均距離越近,這一特征在給定的分類或回歸問題中就越重要。按照分割標(biāo)準(zhǔn),在每棵樹的每處最優(yōu)分割中取得的增益,例如基尼不純度(Gini impurity),是與分割特征直接相關(guān)的重要度測度。每個(gè)特征的評(píng)分值不同(通過累加所有樹得出)。
讓我們深入一些細(xì)節(jié)。
某個(gè)變量導(dǎo)致的平均精確度下降可以通過計(jì)算袋外誤差判定。由于除外或選定某一變量導(dǎo)致的精確度下降約大,該變量的重要性評(píng)分(importance score)就越高。
基尼不純度——或回歸問題中的MSE——的平均下降代表每個(gè)變量對(duì)所得隨機(jī)森林模型節(jié)點(diǎn)的同質(zhì)性的貢獻(xiàn)程度。每次選中一個(gè)變量進(jìn)行分割時(shí),計(jì)算子節(jié)點(diǎn)的基尼不純度,并與原節(jié)點(diǎn)進(jìn)行比較。
基尼不純度是位于0(同質(zhì))到1(異質(zhì))之間的同質(zhì)性評(píng)分。為每個(gè)變量累加分割標(biāo)準(zhǔn)對(duì)應(yīng)值的變動(dòng),并在計(jì)算過程的最后加以正則化。基尼不純度下降較高標(biāo)志著基于該變量進(jìn)行的分割可以得到純度更高的節(jié)點(diǎn)。
以上可以用分析形式表達(dá)為:
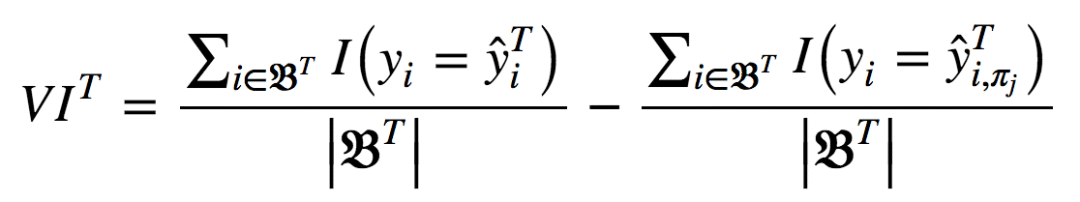
其中,πj表示選中或排除特征。當(dāng)xj不在樹T中時(shí),VIT(xj) = 0。
現(xiàn)在,我們可以給出集成的特征重要性計(jì)算公式。
未經(jīng)正則化:
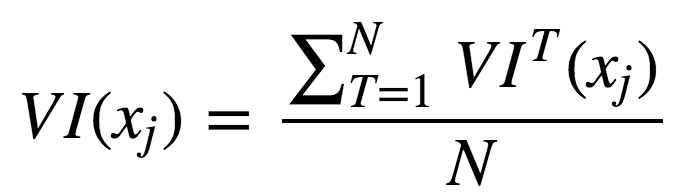
使用標(biāo)準(zhǔn)差正則化后:
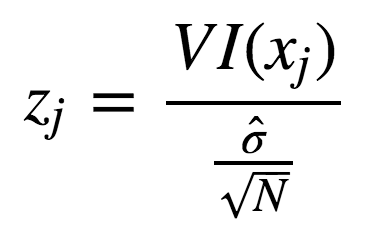
實(shí)際操作例子
讓我們考慮一項(xiàng)調(diào)查結(jié)果,關(guān)于Booking.com和TripAdvisor.com上列出的旅館。這里的特征是不同類別(包括服務(wù)質(zhì)量、房間狀況、性價(jià)比等)的平均評(píng)分。目標(biāo)變量為旅館在網(wǎng)站上的總評(píng)分。
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
from matplotlib import rc
font = {'family': 'Verdana',
'weight': 'normal'}
rc('font', **font)
import pandas as pd
import numpy as np
from sklearn.ensemble.forest importRandomForestRegressor
hostel_data = pd.read_csv("../../data/hostel_factors.csv")
features = {"f1":u"Staff",
"f2":u"Hostel booking",
"f3":u"Check-in and check-out",
"f4":u"Room condition",
"f5":u"Shared kitchen condition",
"f6":u"Shared space condition",
"f7":u"Extra services",
"f8":u"General conditions & conveniences",
"f9":u"Value for money",
"f10":u"Customer Co-creation"}
forest = RandomForestRegressor(n_estimators=1000, max_features=10,
random_state=0)
forest.fit(hostel_data.drop(['hostel', 'rating'], axis=1),
hostel_data['rating'])
importances = forest.feature_importances_
indices = np.argsort(importances)[::-1]
num_to_plot = 10
feature_indices = [ind+1for ind in indices[:num_to_plot]]
plt.figure(figsize=(15,5))
plt.title(u"Feature Importance")
bars = plt.bar(range(num_to_plot),
importances[indices[:num_to_plot]],
color=([str(i/float(num_to_plot+1))
for i in range(num_to_plot)]),
align="center")
ticks = plt.xticks(range(num_to_plot),
feature_indices)
plt.xlim([-1, num_to_plot])
plt.legend(bars, [u''.join(features["f"+str(i)])
for i in feature_indices]);
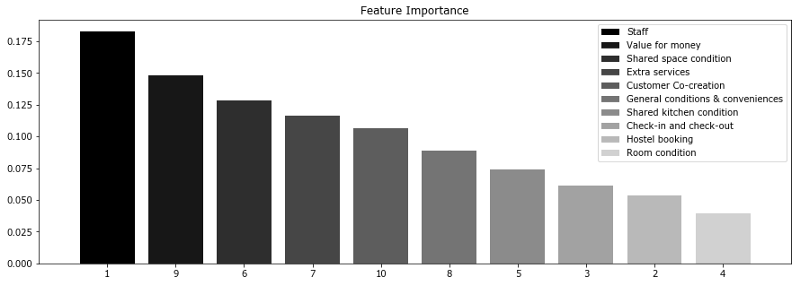
上圖顯示,消費(fèi)者常常更為關(guān)心服務(wù)人員和性價(jià)比。這兩個(gè)因子對(duì)最終評(píng)分的影響最大。然而,這兩項(xiàng)特征和其他特征的差別不是非常大。因此,排除任何特征都會(huì)導(dǎo)致模型精確度的下降。基于我們的分析,我們可以建議旅館業(yè)主重點(diǎn)關(guān)注服務(wù)人員培訓(xùn)和性價(jià)比。
-
集成
+關(guān)注
關(guān)注
1文章
177瀏覽量
30583 -
隨機(jī)森林
+關(guān)注
關(guān)注
1文章
22瀏覽量
4351 -
Bagging
+關(guān)注
關(guān)注
0文章
2瀏覽量
2323
原文標(biāo)題:機(jī)器學(xué)習(xí)開放課程(五):Bagging與隨機(jī)森林
文章出處:【微信號(hào):jqr_AI,微信公眾號(hào):論智】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
深入淺出解析低功耗藍(lán)牙協(xié)議棧
《零基礎(chǔ)開發(fā)AI Agent——手把手教你用扣子做智能體》
隨機(jī)化在PCIe IDE驗(yàn)證中的重要性






 深入淺出地介紹集成、Bagging、隨機(jī)森林、特征重要性
深入淺出地介紹集成、Bagging、隨機(jī)森林、特征重要性











評(píng)論