編者按:如下圖所示,這是一個非常基礎的分類問題:空間中存在兩個高維聚類(兩簇藍點),它們被一個超平面分離(橙線)。其中兩個白色圓點表示兩個聚類的質心,它們到超平面的歐氏距離決定了模型的性能,而橙色虛線正是它們垂直的方向。
在這類線性分類問題中,通過調整L2正則化的水平,我們能不斷調整這個垂直方向的角度。但是,你能解釋這是為什么嗎?

許多研究已經證實,深層神經網絡容易受對抗樣本影響。通過在圖像中加入一些細微擾動,分類模型會突然臉盲,開始指貓為狗、指男為女。如下圖所示,這是一個美國演員人臉分類器,輸入一張正常的Steve Carell圖像后,模型認為照片是他本人的概率有0.95。但當我們往他臉上稍微加了點料,他在模型眼里就成了女演員Zooey Deschanel。
這樣的結果令人憂心。首先,它挑戰了一個基礎共識,即新數據的良好泛化和模型對小擾動的穩健性(魯棒性)是相互促進的,上圖讓這個說法站不住腳。其次,它會對現實應用構成潛在威脅,去年11月,MIT的研究人員曾把擾動添加到3D物品上,成功讓模型把海龜分類成槍支。鑒于這兩個原因,理解這種現象并提高神經網絡的穩健性已經成為學界的一個重要研究目標。
近年來,一些研究人員已經探索了幾種方法,比如描述現象、提供理論分析和設計更強大的架構,對抗訓練現在也已經成了新的正則化技術。不幸的是,它們都沒能從根本上解決這個問題。面對這一困難,一種可行的思路是從最基礎的線性分類出發,去逐步分解問題的復雜度。
玩具問題
在線性分類問題中,我們一般認為對抗性擾動就是高維空間中的點積。對此,一種非常普遍的說法是:我們可以在高維問題中對輸入進行大量無限小的改變,從而使輸出發生巨變。但這種說法其實是有問題的。事實上,當分類邊界靠近數據流形時,對抗樣本依然存在——換句話說,它獨立于圖像空間維度。
建模
讓我們從一個最小的玩具問題開始:一個二維圖像空間,其中每個圖像都是關于a和b的函數。
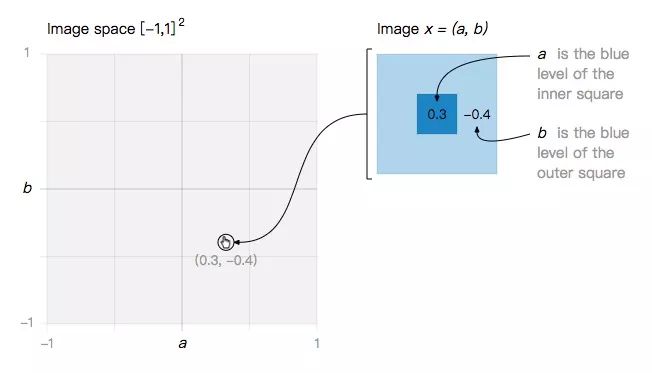
在這個簡單的圖像空間內,我們定義兩類圖像:

它們可以用無數個線性分類器進行分類,比如下圖的Lθ:
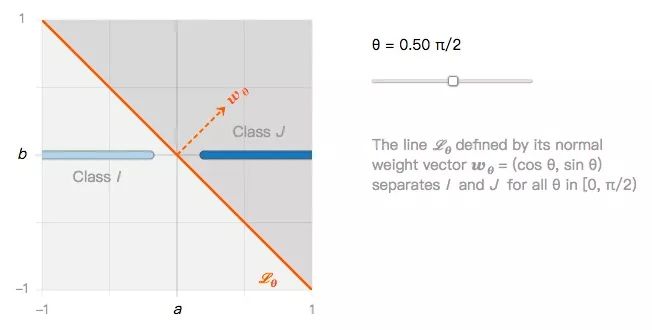
由此我們可以提出第一個問題:如果所有線性分類器都能很好地分類I類圖像和J類圖像,那它們是否也能同樣穩健地分類圖像擾動?
投影和鏡像
假設x是I中的一張圖像,它距離J類圖像的最近距離是它到分類邊界的投影,也就是x到Lθ的垂直距離:

當x和xp距離非常近時,我們把xp看做x的一個對抗樣本。聯系第一個問題,顯然,xp被分類為I的置信度非常低,并不穩健。那么有沒有置信度高的對抗樣本呢?在下圖中,我們根據之前的距離找到了x在J中的鏡像圖像xm:

不難理解,x和xm到分類邊界的距離是一樣的,它們的分類置信度也應該相同。
基于鏡像構建關于θ的函數
讓我們回到之前的玩具問題。有了圖像x和它的鏡像圖像xm,我們可以據此構建一個包含θ的函數。
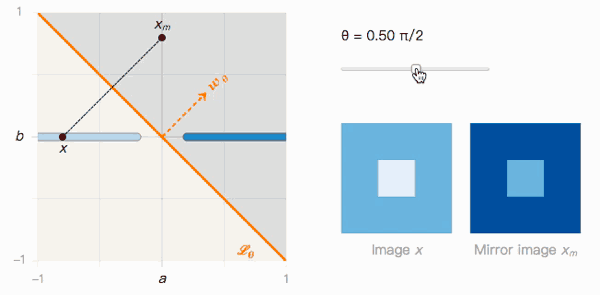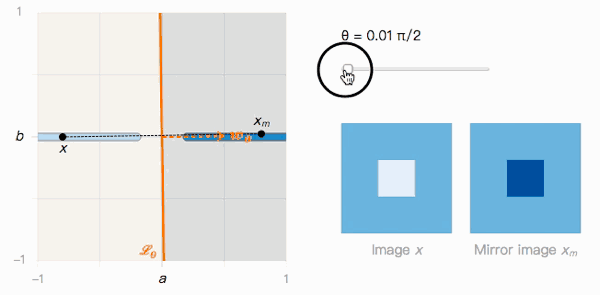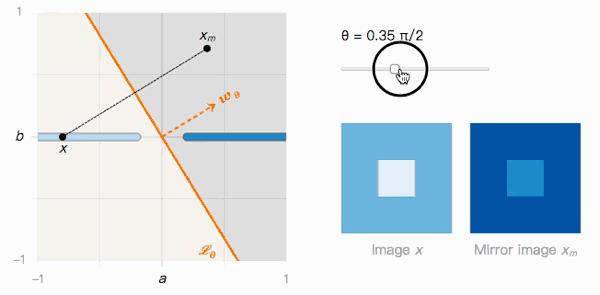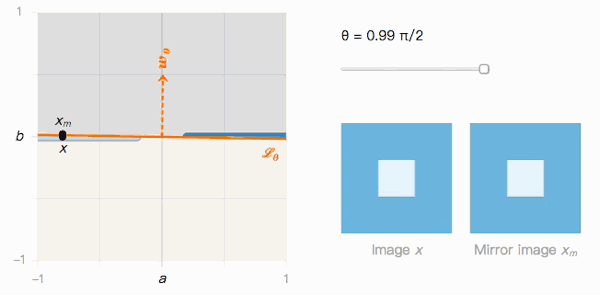
如上圖所示,x到xm的距離取決于分類邊界的夾角θ。我們來觀察一下它的兩個極值:

當θ=0時,Lθ沒有受到對抗樣本影響。x被分類為I的置信度很高,xm被分類為J的置信度也很高,我們可以輕松區分兩者。
當θ→π/2時,Lθ很明顯受到對抗樣本影響。x被分類為I的置信度很高,xm被分類為J的置信度也很高,但它們在視覺上幾乎不可區分。
這就帶來了第二個問題:如果Lθ傾斜的越厲害,對抗樣本存在的幾率就越高,那事實上究竟是什么在影響Lθ?
過擬合和L2正則化
對于這個問題,本文的假設是標準線性模型,比如SVM、邏輯回歸,是因為過擬合訓練集中的噪聲數據才導致過度傾斜的。Huan Xu等人在論文Robustness and Regularization of Support Vector Machines中的理論結果支持了這一假設,認為分類器的穩健性和正則化有一定關聯。
要證明這一點不難,我們來做個實驗:L2正則化是否可以削弱對抗樣本的影響?
設訓練集中存在一個噪聲數據點p:
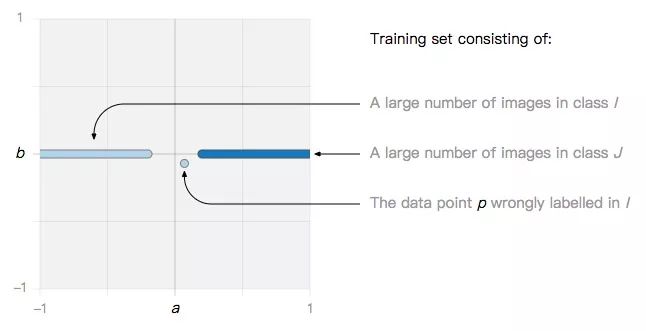
如果我們用的算法是SVM或邏輯回歸,最后可能會觀察到這兩種情況。
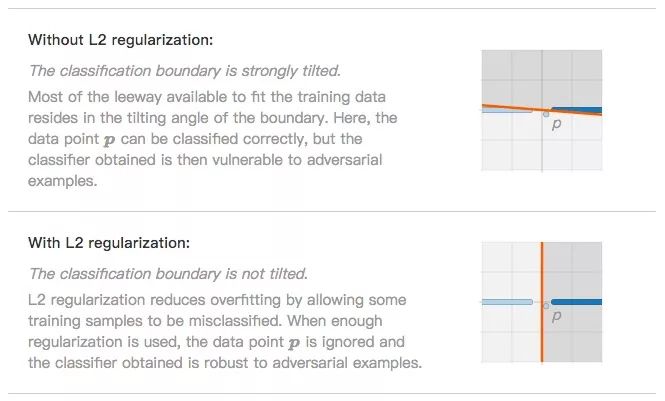
分類邊界嚴重傾斜(無L2正則化)。為了盡量擬合數據點,分類邊界會努力傾斜,讓模型最終能準確分類p。這時分類器是過擬合的,也更易于受到對抗樣本影響。
分類邊界不傾斜(L2正則化)。L2正則化防止過擬合的思路是允許一小部分數據被分類錯誤,如噪聲數據p。忽略它后,分類器在面對對抗樣本時更穩健了。
看到這里,也許有人會有異議:上述數據是二維的,它和高維數據又有什么關系?
線性分類中的對抗樣本
之前我們得出了兩個結論:(1)分類邊界越靠近數據流形,越容易出現對抗樣本;(2)L2正則化可以控制邊界的傾斜角度。雖然都是基于二維圖像空間提出的,但對于一般情況,它們實際上都是成立的。
縮放損失函數
讓我們從最簡單的開始。L2正則化就是在損失函數后再加一個正則化項,不同于L1把權重往0靠,L2正則化的權重向量是不斷下降的,因此它也被稱為權重衰減。
建模
設I和J為高維圖像空間Rd中的兩類圖像,C為線性分類器輸出的超平面邊界,它和權重向量w和偏置項b有關。x是Rd中的一幅圖,則x到C的原始得分為:
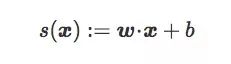
這個原始得分其實是x關于C的符號距離(signed distance,帶正負號):
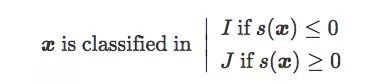
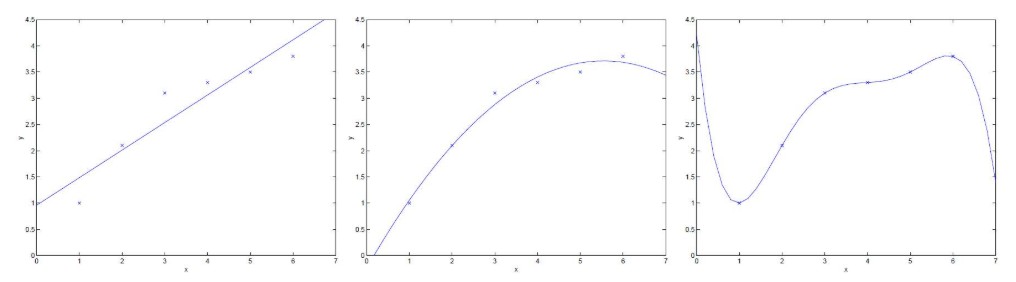
設存在一個包含n對(x,y)的訓練集T,其中x是圖像樣本,當x∈I時,y=-1;當x∈J時,y=1。下面是T的三種分布:

分類器C的期望風險R(w,b),就是對訓練集T的平均懲罰:
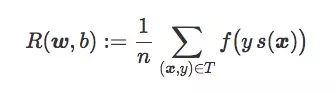
通常情況下,我們訓練線性分類器時會用合適的損失函數f找到權重向量w和偏置項b,使R(w,b)最小。在一般二元分類問題中,下面是三個值得關注的損失函數:
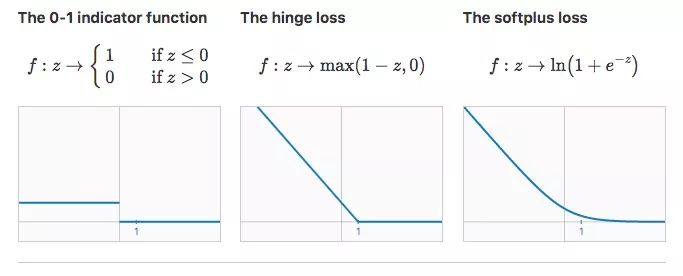
如上圖所示,對于第一個損失函數,分類器的期望風險就是它的分類錯誤率。從某種意義上來說,這個損失函數是最理想的,因為我們只需最小化誤差就能達成目標。但它的缺點是導數始終為0,我們不能在這個基礎上用梯度下降。
事實上,上述問題現在已經被解決了,一些線性回歸模型使用改進版損失函數,比如SVM的hinge loss和邏輯回歸的softplus loss。它們不再繼續在分類錯誤數據上使用固定懲罰項,而是用了一個嚴格遞減的懲罰項。作為代價,這些損失函數也會給正確分類的數據帶去副作用,但最終能保證找出一個較為準確的分類邊界。
縮放參數‖w‖
之前介紹符號距離s(x)時,我們沒有詳細說明它的縮放參數w。如果d(x)是x到C的歐氏距離,我們有:
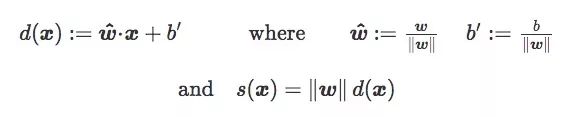
因此,‖w‖也可以被看作損失函數的縮放參數:

也就是:f‖w‖:z→f(‖w‖×z) 。
可以發現,這個縮放對之前提到的第一個損失函數沒有影響,但對hinge loss和softplus loss卻影響劇烈。

值得注意的是,對于縮放參數的極值,后兩個損失函數變化一致。

更確切地說,兩種損失函數都滿足:
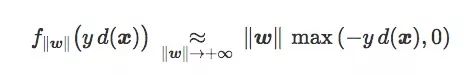
方便起見,我們將錯誤分類的數據定義為:

所以期望風險可以被改寫成:

這個表達式包含了一個我們稱之為“誤差距離”的概念:

它是正的,可以解釋為每個訓練樣本被C錯誤分類的平均距離(對正確分類數據的貢獻為零)。它與訓練誤差有關,但不完全等同。
最后,我們可以得到:
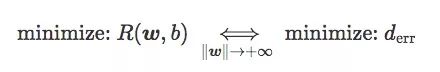
換句話說,當‖w‖足夠大時,最小化hinge loss和softplus loss的期望風險就等于最小化誤差距離,也就是最小化訓練集上的錯誤率。
小結
綜上所述,通過在損失函數后加上正則化項,我們能控制‖w‖的值,從而輸出正則化的損失。

一個較小的正則化參數λ會讓‖w‖失控增大,一個較大的λ會讓‖w‖縮小。
總之,線性分類(SVM和邏輯回歸)中使用的兩個標準模型在兩個目標之間取得平衡:它們在正則化參數低時最小化誤差距離,并且在正則化系數高時最大化對抗距離。
對抗距離和傾斜角度
看到這里,我們又接觸了一個新詞——“對抗距離”——對抗性擾動的穩健性的度量。和之前二維圖像空間的例子一樣,它可以表示為包含單個參數的函數,這個參數即分類邊界和最近的質心分類器之間的角度。
對于訓練集T,如果我們按圖像類別I和J把它分成TI和TJ,我們可以得到:
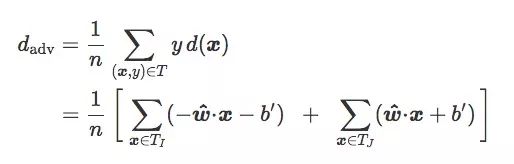
如果TI和TJ是均等的(n=2nI=2nJ):
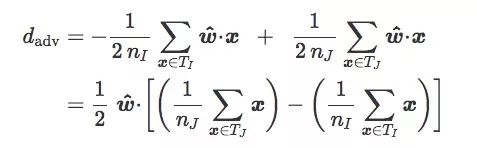
設TI和TJ的質心分別是i和j:

現在有一個離分類邊界最近的質心分類器,它的法向量是z^=(j?i)/‖j?i‖:
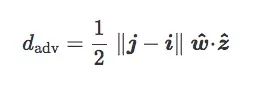
最后,我們將包含w^和z^的平面稱為C的傾斜平面,我們稱之為w^和z^之間的夾角θ為C的傾斜角度:

這個等式的幾何含義如下圖所示:

綜合以上推算,在給定訓練集T上,如果兩個質心‖j?i‖之間的距離是個固定值,那對抗距離dadv僅取決于傾斜角θ。通俗地講:
當θ=0時,對抗距離最大,對抗樣本影響最小;
當θ→π/2時,對抗距離最小,對抗樣本對分類器的影響最大。
最后的話
盡管對抗樣本已經被研究了很多年,盡管它在理論和實踐中都對機器學習領域具有重要意義,但學界對它的研究還非常有限,它對很多人來說還是個迷。這篇文章給出了線性模型下對抗樣本的生成情況,希望能給對這方面感興趣的新人提供一定見解。
可惜的是,現實并沒有文章描述的這么簡單,隨著數據集變大、神經網絡不斷加深,對抗樣本也正變得越來越復雜。根據我們的經驗,模型包含的非線性因素越多,權重衰減似乎就越有用。這個發現可能只是淺層次的,但更深層次的內容將交給不斷涌現的新人來解決。可以肯定的一點是,如果要對這個困難給出一個令人信服的解決方案,我們需要在深度學習中見證一種新的革命性觀念的誕生。
-
神經網絡
+關注
關注
42文章
4810瀏覽量
102918 -
圖像
+關注
關注
2文章
1094瀏覽量
41056 -
分類器
+關注
關注
0文章
153瀏覽量
13413
原文標題:L2正則化視角下的對抗樣本
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
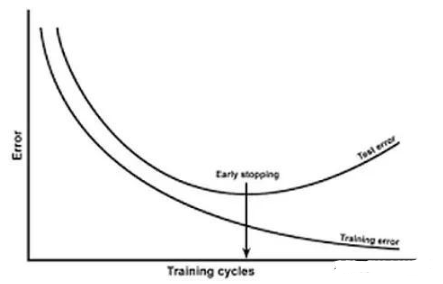
過擬合的概念和用幾種用于解決過擬合問題的正則化方法






 基于鏡像構建關于θ的函數,過擬合和L2正則化
基于鏡像構建關于θ的函數,過擬合和L2正則化










評論