編者按:Feedly聯合創始人、大數據與機器學習主管Kireet Reddy講解了LogSumExp原理。
機器學習中有很多巧妙的竅門,可以加速訓練,提升表現……今天我將討論LogSumExp這一機器學習中常見的模式。首先給出定義:
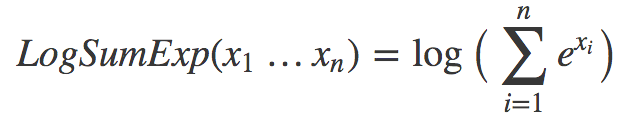
我們什么時候會見到這樣的式子?常見的一個地方是計算softmax函數的交叉熵損失。如果這聽起來冗長難解,那么:1) 習慣一下,ML中太多東西有著瘋狂的名字;2) 直接意識到這沒什么復雜的。有必要的話可以看看斯坦福cs231n的出色講解,或者,就本文而言,只需了解softmax是這樣一個函數就可以:
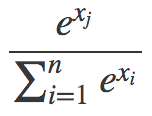
其中,分子中的xj是分母中的一個值(其中一個xi)。所以softmax做的基本上是對一些值取冪,然后歸一化,使得所有xj的可能值總和為1,以生成所需的概率分布。
所以,你可以把softmax函數看成一種接受任何數字并轉換為概率分布的非線性方法。至于交叉熵,只需了解它是對函數取對數。這就涌現出了LogSumExp模式:
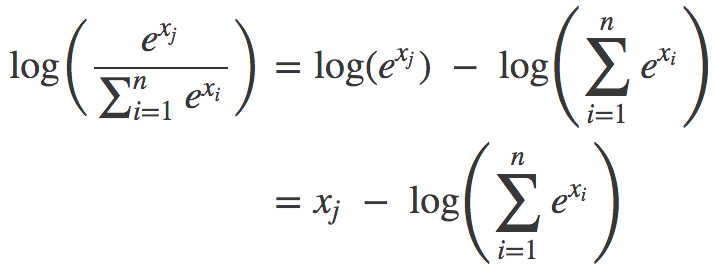
為什么這是一種生成概率分布的好方法,也許看起來有點神秘。目前而言,不妨把這當成是信條。
數值穩定性
我們還是接著談談LogSumExp吧。首先,從純數學的角度來說,LogSumExp沒什么特別的。但是,當我們討論計算機上的數學時,LogSumExp就特別起來了。原因在于計算機表示數字的方式。計算機使用固定數目的位元表示數字。幾乎所有時刻這都沒什么問題,但是,因為不可能用固定數目的位元精確表示數字的無限集合,所以有時這會導致誤差。
讓我們舉例演示這個問題,從xi中取樣兩個樣本:{1000, 1000, 1000}和{-1000, -1000, -1000}。將這兩個序列傳入softmax函數會得到同一概率分布{1/3, 1/3, 1/3},然后1/3的對數是一個合理的負數。現在讓我們嘗試用Python算下求和中的一項:
>>> import math
>>> math.e**1000
Traceback (most recent call last):
File "", line 1, in
OverflowError: (34, 'Result too large')
哎喲。也許-1000的運氣要好些:
>>> math.e**-1000
0.0
也不對勁。所以我們碰到了某種數值穩定性問題,即使看起來合理的輸入值也會導致溢出。
迂回方案
幸運的是,人們找到了一個很好的緩解方法,根據冪的乘法法則:
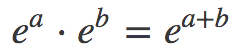
以及對數的和差公式:
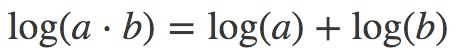
我們有:
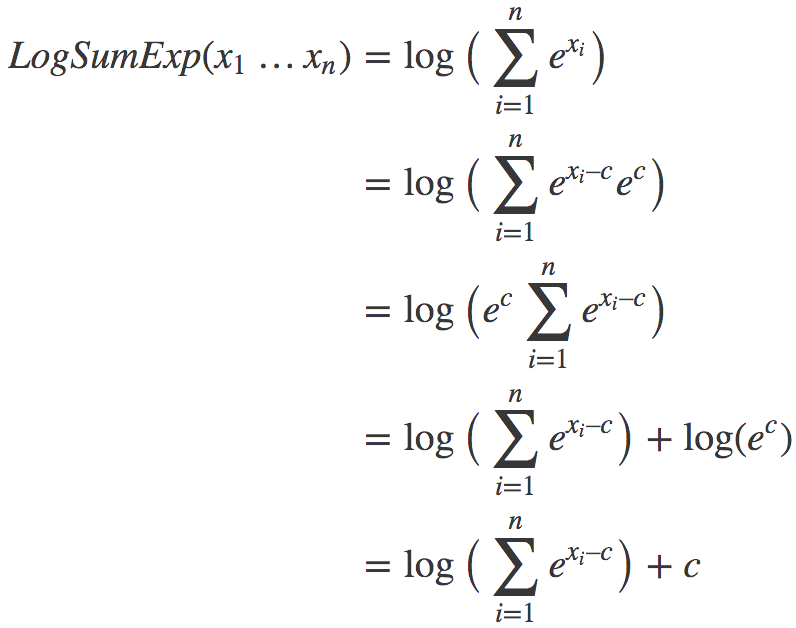
上述變換的關鍵在于,我們引入了一個不牽涉log或exp函數的常數項c。現在我們只需為c選擇一個在所有情形下有效的良好的值。結果發現,max(x1…xn)很不錯。
由此我們可以構建對數softmax的新表達式:
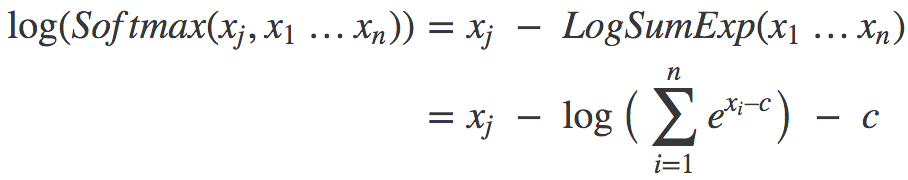
現在我們用這個新表達式計算之前的兩個樣本。對{1000, 1000, 1000}而言,c = 1000,所以xi-c恒為零,代入上式,我們有:
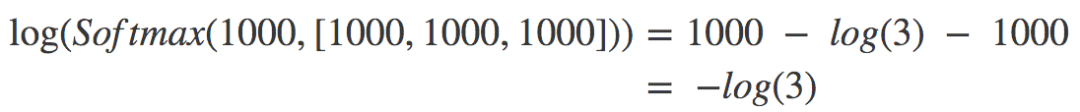
log(3)是一個很合理的數字,計算機計算起來毫無問題。所以上面的樣本沒問題。同理,{-1000, -1000, -1000}也沒問題。
關鍵點
思考一些例子后,我們可以得到以下結論:
如果xi的值都不會造成穩定性問題,那么“樸素”版本的LogSumExp可以很好地工作。但“改良”版同樣可以工作。
如果至少有一個xi的值很大,那么樸素版本會溢出,改良版不會。其他類似的大數值xi同理,而并不大的那些xi,基本上逼近零。
對于絕對值較大的負數,翻轉下符號,道理是一樣的。
所以,盡管并不完美,我們在大多數情況下能夠得到相當合理的表現,而不會溢出。我創建了一個簡單的python腳本,這樣,你可以通過親自試驗驗證這一點:git.io/fx5Vx
LogSumExp是一個巧妙的竅門,分解了它的機制后,實際上相當容易理解。一旦了解了LogSumExp和數值穩定性問題,你就不會感到一些庫的文檔和源代碼難以理解了。
為了鞏固記憶(同時操練下數學),我建議你過一段時間嘗試自行推導下數學,并在腦海中設想各種例子,做下推理。接著運行我的代碼(或者自己動手重寫),以驗證你的直覺。
-
函數
+關注
關注
3文章
4372瀏覽量
64367 -
機器學習
+關注
關注
66文章
8496瀏覽量
134209
原文標題:機器學習常見模式LogSumExp解密
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄





 LogSumExp這一機器學習中常見的模式
LogSumExp這一機器學習中常見的模式

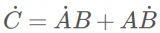
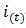











評論