什么是異常檢測?
異常檢測是一個發現“少數派”的過程,由于它們與大多數數據不一樣而引起我們的注意。在幾個典型場景中,異常數據能為我們關聯到一些潛在的問題,如銀行欺詐行為、藥品問題、結構缺陷、設備故障等。這些關聯關系能幫助我們挑出哪些點可能是異常的,從商業角度來看,查出這些事件是非常有價值的。
這樣就引出我們的主要目標:我們如何分辨每個點是正常還是異常呢?在一些簡單的場景中,如下圖所示,數據可視化就可以給出重要信息。
圖 1:兩個變量的異常
在這個二維數據(X 和 Y)的例子中,判斷異常點是非常容易的,只需要觀察數據點在二維平面上的分布即可。然而,觀察右圖可以發現,只觀察一個變量是無法看出異常的,只有把變量 X 和變量 Y 結合起來觀察,才能發現異常點。當我們把數據維度從 2 提升到 10-100,這件事情就極其復雜了,實際場景的異常檢測也是如此。
什么是狀態監控?
無論任何機器,旋轉電機(泵、壓氣機、燃氣或蒸汽輪機等)或非旋轉機器(熱交換器、分裂蒸餾塔、閥門等),都會最終出現運轉異常的情況。出現這種情況時,機器并不一定是徹底壞掉了,可能只是無法以最佳狀態運轉,它可能需要進行維修以恢復完全的運轉能力。簡而言之,識別設備的“健康狀態”就是狀態監控領域所研究的問題。
在狀態監控中,最常用的方法是觀測機器的每個傳感器,并對其設置一個最小值和最大值。如果當前值在所設置范圍之內,說明機器運轉正常。如果當前值超出范圍,系統會給出預警信號,提醒機器運轉不正常。
對機器硬性施加報警閾值這一過程,會導致系統發出大量假的預警信號,即機器運轉正常時卻收到了異常報警。同時也存在預警信號遺漏的問題,即機器運轉異常卻沒有收到警示。第一個問題不僅浪費時間精力,也影響機器壽命。第二個問題更為嚴重,可能導致機器損壞,進而損失大量維修費用和生產損失。
而兩個問題都源于一個原因:設備的健康程度是一個高維的復雜問題,不能依賴于某個單獨的指標進行判斷(和圖 1 展示的異常檢測問題同理)。我們必須結合考慮多個檢測值,從而獲得一個更為真實的信號。
主要方法
說到異常檢測,很難把機器學習和統計分析全部覆蓋,我會避免在理論知識上過于深入(但會提供一些有詳細介紹的鏈接)的同時介紹一些常用方法。如果你對機器學習和統計分析在狀態監控方面的實際應用更感興趣,可以往下看“狀態監控實例”部分。
方法一:多變量統計分析
使用主成分分析法進行降維:PCA
處理高維數據總是充滿挑戰的,減少變量個數(降維)的方法有很多。其中最主要的方法是主成分分析法(PCA, principal component analysis),該方法將數據映射到一個低維空間,使數據在低維空間的方差最大化。在實際應用中,需要建立數據的協方差矩陣,并計算矩陣的特征向量。對應最大特征值(即主要成分)的特征向量可用作重新構建原數據集。如今原特征空間被減小了(部分數據丟失了,但保留了最重要的信息),得到了由部分特征向量構成的空間。
降維:
https://en.wikipedia.org/wiki/Dimensionality_reduction
PCA:
https://en.wikipedia.org/wiki/Principal_component_analysis
協方差矩陣:
https://en.wikipedia.org/wiki/Covariance_matrix
特征向量:
https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors
多變量異常檢測
當處理單變量或兩個變量的異常檢測時,數據可視化常常是一個好的方法。然而,當拓展到高維數據時(同時也是大多數實際應用中的情況),這種方法就會極其難處理。幸運的是,多變量分析可以幫得上忙。
當處理一個數據點的集合時,這些點會有典型的特定分布(如高斯分布)。要想定量地檢測異常點,我們要先計算數據點的概率分布 p(x)。之后出現新的點 x,我們就可以用 p(x) 與閾值 r 作對比了。如果 p(x)
狀態監控場景中的異常檢測很有趣,因為異常可以告訴我們有關被監控設備是否“健康”的訊息:當設備臨近故障或非最優操作所產生的數據,與設備正常運轉所產生的數據在分布上不同。
多變量統計/多元統計:
https://en.wikipedia.org/wiki/Multivariate_statistics
高斯分布:
https://en.wikipedia.org/wiki/Normal_distribution
概率分布:
https://en.wikipedia.org/wiki/Probability_distribution
馬氏距離
試考慮一個數據點是否屬于某一分布的概率問題。第一個步驟是找到質心或者說樣本點的質量中心。直觀上來看,該點離質心越近,越可能屬于這個集合。然而,我們也要注意該集合的范圍大小,這樣我們才能判斷給定的離質心的距離是否值得注意。簡化的方法是去估計樣本點與質心距離的標準差。將其插入標準分布中,我們可以得出數據點是否屬于同一分布的概率值。
上述方法也存在缺陷,我們假設了樣本點相對于質心是球形分布的。如果它們的分布不是球狀的,而是橢圓狀的,我們在判斷測試點是否屬于該集合時,不僅要考慮與質心的距離,還要考慮方向。在那些橢圓短軸的方向上,測試點的距離一定更近,但那些長軸方向上測試點是遠離質心的。從數學角度看,我們可以通過計算樣本的協方差矩陣,來估計出最能代表集合分布的橢圓。馬氏分布是指從測試點到質心的距離除以橢圓在測試點方向上的寬度。
為了使用馬氏距離來判別一個測試點屬于 N 個分類中的哪一個,首先應該基于已知樣本與各個分類的對應情況,來估計每個類的協方差矩陣。在我們的例子中,我們只對“正常”和“異常”兩個類別感興趣,我們使用只包含正常操作狀態的數據作為訓練數據,來計算協方差矩陣。接下來,拿來測試樣本,計算出它們與“正常”類別的馬氏距離,如果距離高于所設置的閾值,則說明該測試點為“異常”。
馬氏距離:
https://en.wikipedia.org/wiki/Mahalanobis_distance
方法二:人工神經網絡
自動編碼器網絡
第二種方法是基于自動編碼器神經網絡。它的基本思想與上面的統計分析相似,但略有差異。
自動編碼器是一種人工神經網絡,通過無監督的方式學習有效的數據編碼。自動編碼器的目的是學習一組數據的表示(編碼),通常用于降維過程。與降維的一層一起,通過學習得到重建層,自動編碼器嘗試將降維層進行編碼,得到盡可能接近于原數據集的結果。
在結構上,最簡單的自動編碼器形式是前饋非循環神經網絡,與許多單層感知器類似,它們構成了包含輸入層、輸出層和用于連接的一個或多個隱藏層的多層感知器(MLP, multilayer perceptron),但輸出層的節點數與輸入層相同,目的是對自身的輸入進行重建。
自動編碼器:
https://en.wikipedia.org/wiki/Autoencoder
人工神經網絡:
https://en.wikipedia.org/wiki/Artificial_neural_network
有效數據編碼:
https://en.wikipedia.org/wiki/Feature_learning
無監督:
https://en.wikipedia.org/wiki/Unsupervised_learning
多層感知器:
https://en.wikipedia.org/wiki/Multilayer_perceptron
圖2:自動編碼器網絡
在異常檢測和狀態監控場景中,基本思想是使用自動編碼器網絡將傳感器的讀數進行“壓縮”,映射到低維空間來表示,獲取不同變量間的聯系和相互影響。(與 PCA 模型的基本思想類似,但在這里我們也允許變量間存在非線性的影響)
接下來,用自動編碼器網絡對表示“正常”運轉狀態的數據進行訓練,首先對其進行壓縮然后將輸入變量重建。在降維過程中,網絡學習不同變量間的聯系(例如溫度、壓力、振動情況等)。當這種情況發生時,我們會看到通過網絡重構后的輸入變量的異常報錯增多了。通過對重構后的報錯進行監控,工作人員能夠收到所監控設備的“健康”信號,因為當設備狀態變差時,報錯會增多。與基于馬氏距離的第一種方法類似,我們在這里使用重建誤差的概率分布來判斷一個數據點是正常還是異常。
狀態監控實例:齒輪軸承故障
在這個部分,我會介紹上述兩個不同方法在狀態監控實例中的應用。由于實際工作中大部分客戶的數據是無法公開的,我們選擇使用 NASA 的數據來展示兩種方法,讀者也可以通過鏈接自行下載。
NASA 數據下載:
http://data-acoustics.com/measurements/bearing-faults/bearing-4/
在該實例中,目的是檢測發動機上的齒輪軸承退化,并發送警告,以幫助工作人員及時采取措施以免齒輪故障。
實驗細節和數據準備
在恒定負載和運行條件下,三個數據集各包含四個軸承運行出現異常的數據。數據集提供了軸承生命周期內的振動測量信號,直到出現故障。前連天的運行數據被用作訓練數據,以表示正常且“健康”的設備。剩余部分的數據包含軸承運轉直到故障的過程,這部分數據用作測試數據,以評估不同方法是否能在運轉故障前檢測到其軸承異常。
方法一:PCA + 馬氏距離
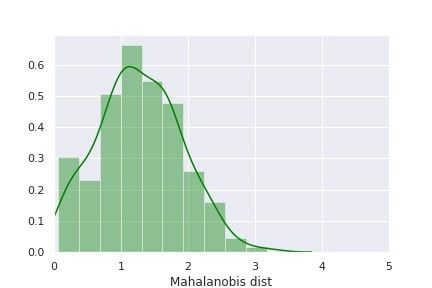
正如本文“技術部分”中所介紹的,第一種方法先進行主成分分析,然后計算其馬氏距離,來辨別一個數據點是正常的還是異常的(即設備退化的信號)。代表“健康”設備的訓練數據的馬氏距離的分布如下圖所示:
圖3:“健康”設備的馬氏距離分布
利用“健康”設備的馬氏距離分布,我們可以設定判斷是否為異常點的閾值。從上面的分布圖來看,我們可以定義馬氏距離大于 3 的部分為異常。這種檢測設備老化的估計方法,需要計算測試集中全部數據點的馬氏距離,并將其與所設置的閾值進行比較,來標記其是否異常。
基于測試數據的模型評估
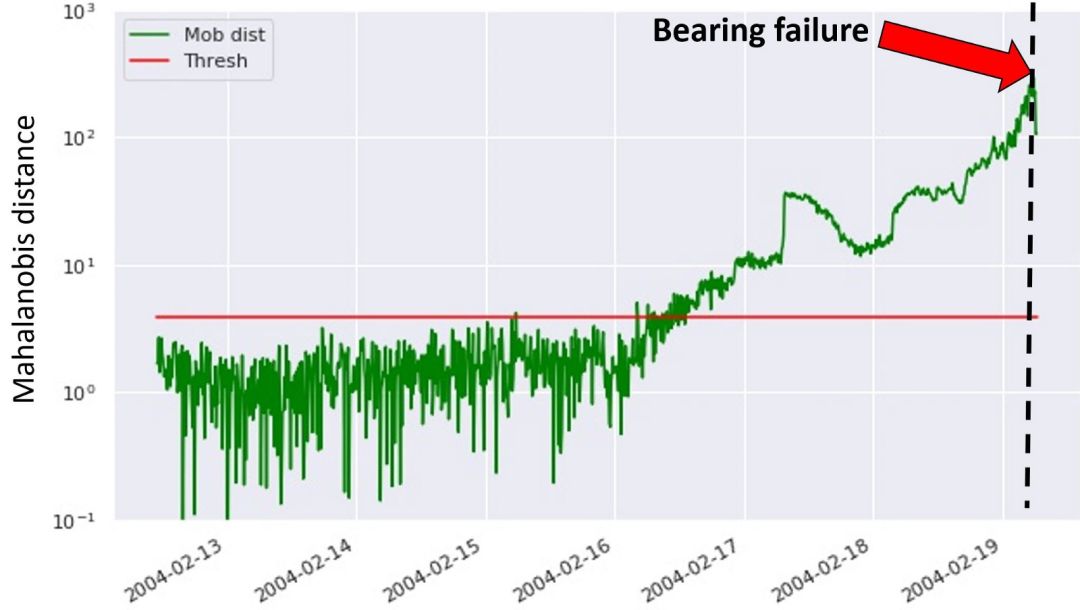
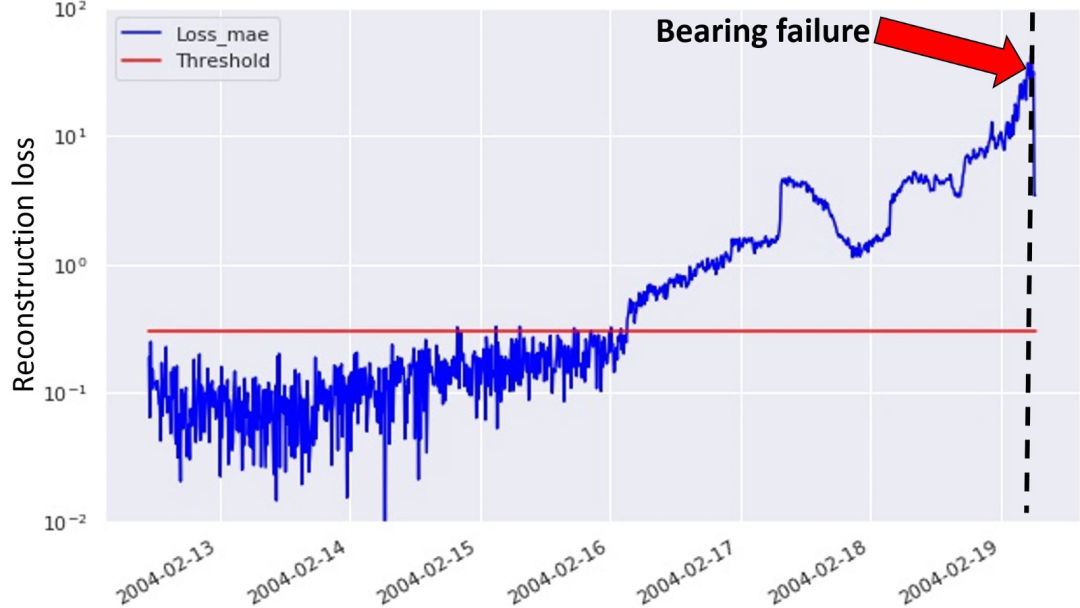
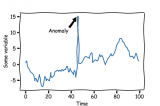
利用上述方法,我們計算測試數據,即運轉直到軸承故障這一時間段內數據的馬氏距離,如下圖所示:
圖 4:利用方法一檢測軸承故障
在上圖中,綠色點對應計算得到的馬氏距離,而紅線表示所設置的異常閾值。軸承故障發生在數據集的最末端,即黑色虛線標記處。這說明第一種方法可以檢測到 3 天后即將發生的設備故障。
現在我們用第二種建模方法做類似的實驗,以評估哪種方法更好。
方法二:人工神經網絡
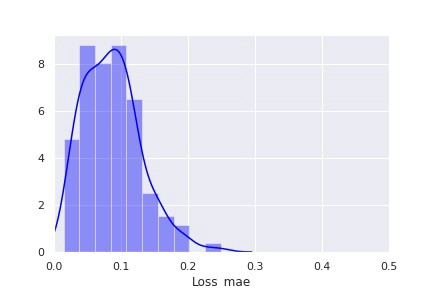
如本文“技術部分”中所寫的,第二種方法包括使用自動編碼器神經網絡來尋找異常點。和第一種方法類似,我們在此也是用模型輸出的分布,用表示“健康”設備的數據作為訓練數據,來進行異常檢測。訓練數據集的重建損失分布如下圖所示:
圖 5::“健康”設備的重建損失分布
利用“健康”設備的重建損失分布,我們可以設置判斷數據是否異常的閾值。由上圖中的分布,我們可以設置損失大于 0.25 的部分為異常。這種檢測設備老化的評估方法包括計算測試集中全部數據點的重建損失,將該損失與所設置閾值作比較,來判別其是否異常。
基于測試數據的模型評估
利用上述方法,我們計算測試數據,即運轉直到軸承故障這一時間段內數據的重建損失,如下圖所示:
圖 6:利用方法二檢測軸承故障
在上圖中,藍色點對應重建損失,而紅線表示所設置的異常閾值。軸承異常發生在數據集的末端,即黑色虛線標記處。這表示該建模方法也能夠檢測到未來 3 天即將發生的設備異常。
總結
綜上所述,兩種不同的方法都能用作異常檢測,在機器實際發生故障前幾天就檢測到即將發生的事故。在現實生活場景中,這項技術可以幫助我們早在故障前就采取預防措施,不僅可以節約開銷,也在設備故障的 HSE 方面具有潛在的重要性。
展望
使用傳感器收集數據的成本越來越低,設備間的連通度也日益提升,從數據中提取有價值的信息變得越來越重要。從大量數據中挖掘模式是機器學習和統計的重要領域,利用這些數據背后隱藏的信息來改善不同領域有極大的可能性。異常檢測和狀態監控只是諸多可能性中的一種。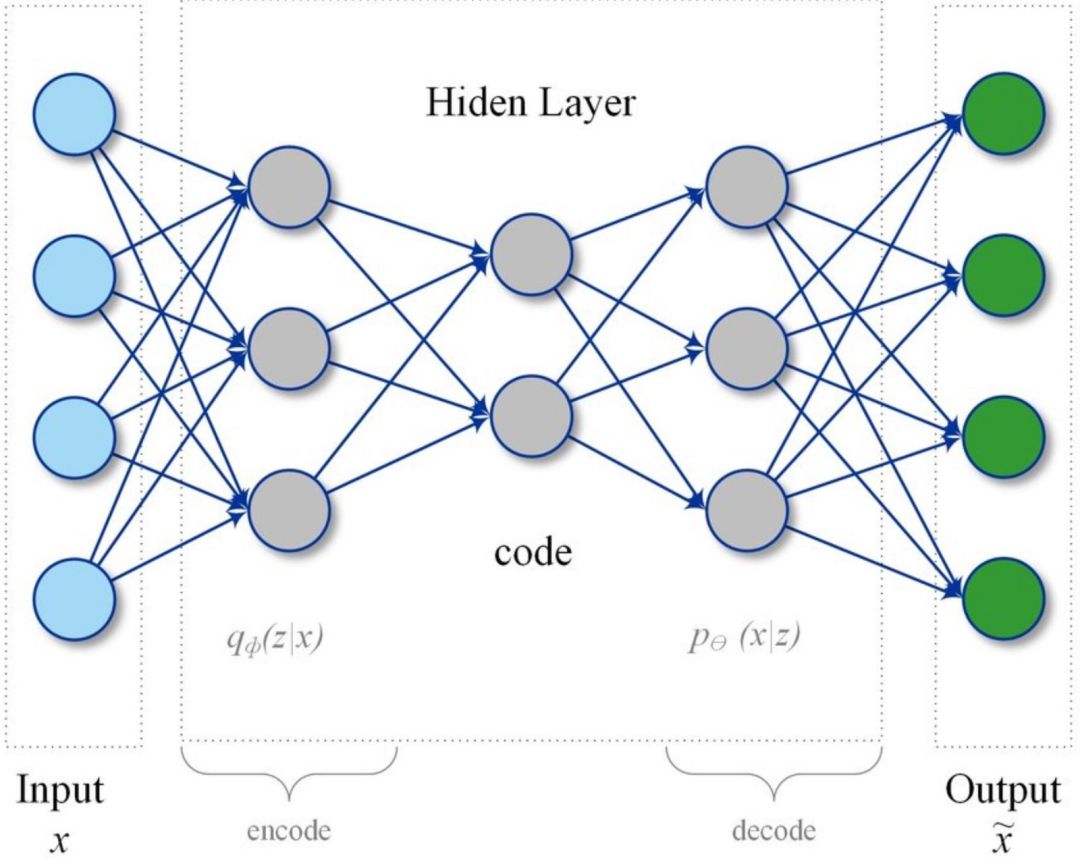
-
數據
+關注
關注
8文章
7233瀏覽量
90816 -
異常檢測
+關注
關注
1文章
43瀏覽量
9804
原文標題:一文掌握異常檢測的實用方法 | 技術實踐
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
基于transformer和自監督學習的路面異常檢測方法分享
基于深度學習的異常檢測的研究方法
基于深度學習的異常檢測的研究方法
基于ME-PGNMF的異常流量檢測方法





 什么是異常檢測_異常檢測的實用方法
什么是異常檢測_異常檢測的實用方法










評論