1.1 電子系統與信號
1.1.1 電子系統
所謂電子系統,通常是指由若干相互聯接、相互作用的基本電路組成的具有特定功能的電路整體。由于大規模集成電路和模擬-數字混合集成電路的大量出現,單個芯片也可以自成一個系統。例如,目前有多種單個芯片構成的數據采集系統產品,芯片內部往往包括多路模擬開關、可編程放大電路、取樣保持電路、模數轉換電路、數字信號傳輸與控制電路等多種功能電路,并且已互相聯接成為一個單片電子系統。這樣的單片系統是功能更為完善的電子系統中的一個組成部分。一個比較復雜而完善的電子系統,往往是由許多個子系統所構成。從結構上來看,它可能是兩組或是多級的。
在許多情況下,電子系統必須與其他物理系統相結合,才能構成完整的實用系統。例如,常見的VCD系統,在光盤上記錄的聲音和圖像信號,是通過激光傳感系統轉化為電信號的,而光盤的同步旋轉和激光探頭的移動則是通過電子系統控制的精密機械系統實現的。
1.1.2 信號及頻譜
一、信號與電信號
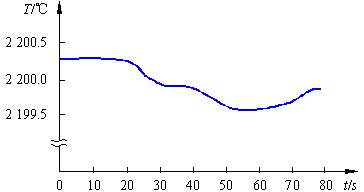
一般地說,信號是信息的載體。例如,聲音信號可以傳達語言、音樂或其他信息,圖像信號可以傳達人類視覺系統能夠接受的圖像信息。上一個知識點中的溫度波動曲線表示的是拉絲塔上加熱爐內溫度隨時間而變化的信號,它是以信號波形表達信息的。
上述聲音信號、圖像信號和溫度信號均為非電信號,無法直接傳遞給電子系統。這些非電物理量需要用適當的傳感器將其轉換為電信號,才能輸入到電子系統中。轉換后得到的電信號就代表相應物理量一定的信息。
|
| |
|
(a) |
(b) |
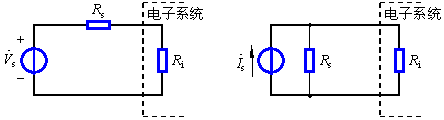
為一般化起見,常把傳感器看作信號源,如圖1所示。其中圖(a)是電壓源形式,Rs是內阻;而圖(b)是電流源。雖然二者是等效的(戴維寧-諾頓等效),并可相互轉換,但是在信號源電阻Rs遠小于電子系統輸入電阻Ri時,使用電壓源形式更為有利,反之則使用電流源形式較方便。類似地,在多級電子電路中對其中某一級進行分析時,前一級電路的輸出信號就是本級的輸入信號,也可以用這兩種信號源之一來簡化表達前級輸出。
二、信號的基本特性
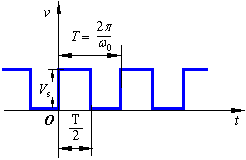
電信號是隨時間變化的電壓或電流。它可用其電壓或電流幅值與時間的函數關系來表示,也可用波形直觀的表達。下面以正弦波電壓信號和方波信號為例說明信號的表達方式及其基本特性。
圖1以最直觀的方式描述了正弦波電壓幅值與時間的函數關系,其數學表達式為
![]() (式1)
(式1)
式中,Vm是正弦波的幅值,w為角頻率,q為初始相角。當w=0時,則為直流電壓信號。當Vm、w、q 均為已知常數時,信號中就不再含有任何未知信息,是最簡單的信號。正因為如此,正弦波信號經常作為標準信號用來對模擬電子電路進行測試。當然實際的信號要比正弦信號復雜得多。
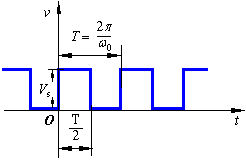
圖2是周期性方波信號,它的時間函數表達式為
|
|
![]() (式2)
(式2)
其中,Vs為方波幅值,T為周期,n為從-¥ 到+¥ 的整數。圖2和式2中的電壓v是時間t的函數,所以稱為方波信號的時域表達方式。
三、信號的頻譜
任意周期函數只要滿足狄利克雷條件都可以展開成傅里葉級數。上一知識點介紹的方波信號(如圖1(a))亦可展開為傅里葉級數表達式:
![]() (1.1.3)
(1.1.3)
?  |
|
(a) |
|
? |
|
(b) |
| 圖1 |
 |
| (a) |
 |
| (b) |
| 圖2 |
式中, ![]() ,
, ![]() 是方波信號的直流分量,
是方波信號的直流分量, ![]() 稱為該方波信號的基波,它的周期
稱為該方波信號的基波,它的周期 ![]() 與方波本身的周期相同。式(1.1.3)中其余各項都是高次諧波分量,它們的角頻率是基波角頻率的整數倍。
與方波本身的周期相同。式(1.1.3)中其余各項都是高次諧波分量,它們的角頻率是基波角頻率的整數倍。
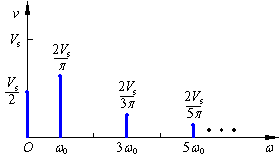
由于正弦函數的單純性,在作信號分析時,可以只考慮其幅值電壓與角頻率的函數關系,于是式(1.1.3)的正弦級數可以表達為圖(b)所示的圖解形式,其中包括直流項(ω=0)和每一正弦分量在相應角頻率處的幅值。像這樣把一個信號分解為正弦信號的集合,得到其正弦信號幅值隨角頻率變化的分布,稱為該信號的頻譜。圖(b)稱為方波信號的頻譜圖,是方波在頻域的表達方式。
從傅里葉級數特性可知,許多周期信號的頻譜都由直流分量、基波分量以及無窮多項高次諧波分量所組成,頻譜表現為一系列離散頻率上的幅值。
上述正弦信號和方波信號都是周期信號。客觀物理世界的信號遠沒有這樣簡單,如果從時間函數來看,往往很難直接用一個簡單的表達式來描述,如圖2(a)所示爐溫變化曲線就是—非周期性時間函數波形。
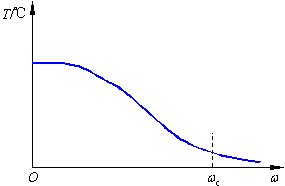
對于非周期信號,運用傅里葉變換可將其表達為—連續頻率函數形式的頻譜,它包含了所有可能的頻率(0≤ω<∞)成分。圖2(b)示意出圖2(a)的頻譜函數。實際物理世界的各種非周期信號,隨角頻率上升到一定程度,其頻譜函數總趨勢是衰減的。當選擇適當的ωc(截止角頻率)點把頻率高端截斷時,并不過多地影響信號的特性。通常把保留的部分稱為信號的帶寬。
由上分析可知,信號的頻域表達方式可以得到某些比時域表達方式更有意義的參數。信號的頻譜特性是電子系統有關頻率特性的主要設計依據。
確定一個任意非周期信號的頻譜在計算機普及應用之前并非易事。自從快速傅里葉變換(FFT)算法出現以后,人們可以用計算機將非周期時間函數信號的頻譜函數迅速求出。在PSPICE程序中就包含有FFT軟件,供讀者分析信號和電路的頻率特性。在某些現代電子設備中,甚至把FFT軟件裝入其中,可在程序控制下向實際電路輸入端注入已知波形的非周期信號,如矩形單脈沖,然后通過比較電路輸出端和輸入端的頻譜函數,直接計算出電路的頻率響應特性。這種快速測試電路頻率響應的方法經常用于電子裝置的自動生產線上,也可以安裝在所謂智能儀器中,用于對儀器本身的自校正和故障自診斷。
1.1.3 模擬信號與數字信號
一、模擬信號
模擬信號的特點是,在時間上和幅值上均是連續的,在一定動態范圍內可能取任意值。從宏觀上看,我們周圍的世界大多數物理量都是時間連續、數值連續的變量。
在信號分析中,按時間和幅值的連續性和離散性把信號分為4類:
(1)時間連續、數值連續信號;
(2)時間離散、數值連續信號;
(3)時間離散、數值離散信號;
(4)時間連續、數值離散信號。
其中第(1)類即前面所述的模擬信號。
處理模擬信號的電子電路稱為模擬電路。本課程主要討論各種模擬電子電路的基本概念、基本原理、基本分析方法及基本應用。
二、數字信號
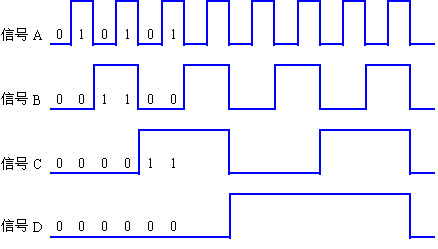
數字系統(如微處理器系統)中運行的信號都是數字信號。從時間函數波形看,它們只存在高、低兩種電平的相互轉換,這兩種電平分別代表了二元編碼中的1和0。圖1是一組數字信號的實例。
處理數字信號的電子電路稱為數字電路。
|
|
 電子發燒友App
電子發燒友App











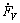
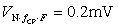
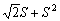
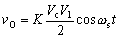
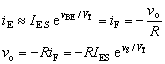
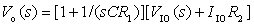










評論