十進制有權碼
是指表示一個十進制數位的4位基2碼的每一位有確定的位權。
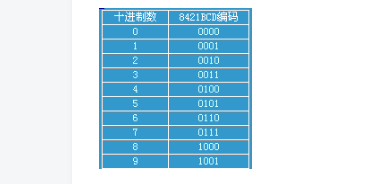
用得最普遍的是8421碼,即4個基2碼位的權從高向低分別為8、4、2和1,使用基2碼的0000、0001、…1001這10種組合,分別表示0到9這十個值。這種編碼的優點是這4位基2碼之間滿足二進制的規則,而十進制數位之間則是十進制規則,故稱這種編碼為以二進制編碼的十進制(Binary Coded Decimal)數,簡稱BCD碼或二-十進制碼。另一個優點是在數字符的ASCII碼與這種編碼之間的轉換方便,即取每個數字符的ASCII碼的低4位的值便直接得到該數字的BCD碼,入/出操作簡便。在計算機內實現BCD碼之間的算術運算要復雜一些,在某些情況下,需要對加法運算的結果進行修正。修正規則是:
若兩個8421碼數相加之和等于或小于1001,即10進制的9,不需要修正;
若相加之和在10到15之間,一方面應向高位產生一進位,本位還要進行加6修正,進位是在進行加6修正時產生的;
若相加之和在16和18之間時,向高位的進位會在相加過程中自己產生,對本位還需進行加6修正。下面給出三種情況下的具體例子。
例如,1+8=9的運算結果是正確的,不必修正。
0 0 0 1
+)1 0 0 0 (1)10+(8)10=(9)10
1 0 0 1
而4+9的結果就必須用 +6 修正,進位是在修正過程中產生的。
0 1 0 0
+)1 0 0 1 (4)10+(9)10 =(1)10 (3)10
1 1 0 1
+) 0 1 1 0
1 0 0 1 1
而7+9的結果也必須用 +6 修正,進位是在相同加過程中產生的。
0 1 1 1
+)1 0 0 1 (7)10+(9)10 =(1)10(6)10
1 0 0 0 0
+) 0 1 1 0
1 0 1 1 0
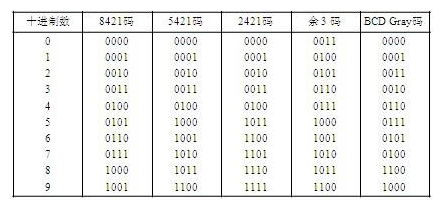
另外幾種有權碼,如2421、5211、84-2-1、4311碼(表2.9),也都是用4位有權基2碼表示一個十進制數位,但這4位基2碼之間并不符合二進制規則。這幾種有權碼的特性表現為:
當采用2421、5211和4311編碼時,任何兩個十進制數位相加產生10或大于10的結果,相應的基2碼相加會向高一位產生進位,有利于實現逢十進位的計數和加法規則。
任何兩個相加之和等于9的十進制數位的基2碼,互為反碼,即滿足十進制數按9互補(9's Complement)的關系,有利于簡化減法處理。表2.9給出的是上面提到的十進制數位的編碼方案。
表2.9 四位有權碼
|
十進制數 |
8421碼 |
2421碼 |
5211碼 |
840201碼 |
4311碼 |
 電子發燒友App
電子發燒友App












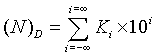










評論