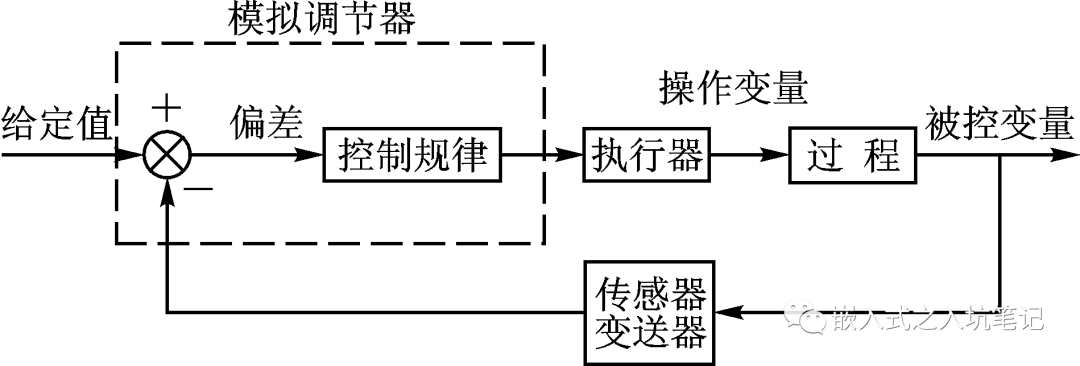
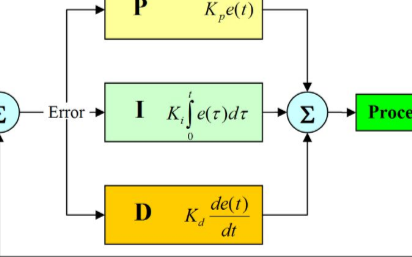
在過程控制中，按偏差的比例(P)、積分(I)和微分(D)進行控制的PID控制器(亦稱PID調節器)是應用最為廣泛的一種自動控制器。它具有原理簡單，易于實現，適用面廣，控制參數相互獨立，參數的選定比較簡單等優點;而且在理論上可以證明，對于過程控制的典型對象──“一階滯后+純滯后”與“二階滯后+純滯后”的控制對象，PID控制器是一種最優控制。PID調節規律是連續系統動態品質校正的一種有效方法，它的參數整定方式簡便，結構改變靈活(PI、PD、…)。

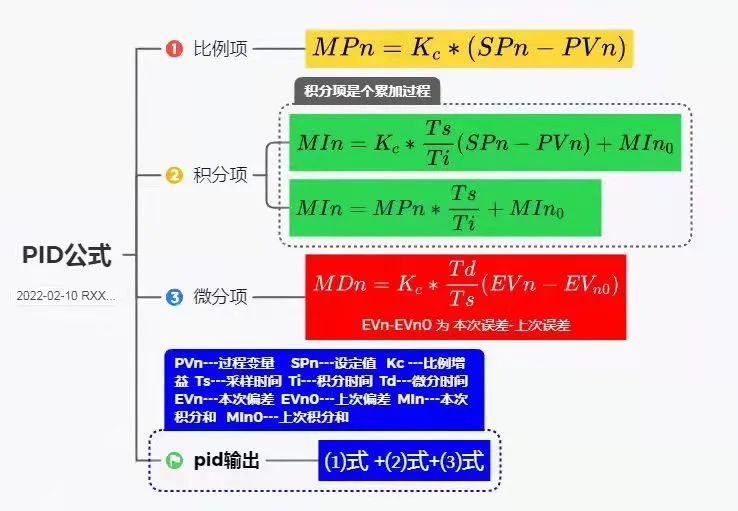
　　PID增量式算法

　　離散化公式：

　　注：各符號含義如下

　　u(t);;;;; 控制器的輸出值。

　　e(t);;;;; 控制器輸入與設定值之間的誤差。

　　Kp;;;;;;; 比例系數。

　　Ti;;;;;;; 積分時間常數。

　　Td;;;;;;; 微分時間常數。

　　T;;;;;;;; 調節周期。

　　對于增量式算法，可以選擇的功能有：

　　(1) 濾波的選擇

　　可以對輸入加一個前置濾波器，使得進入控制算法的給定值不突變，而是有一定慣性延遲的緩變量。

　　(2) 系統的動態過程加速

　　在增量式算法中，比例項與積分項的符號有以下關系：如果被控量繼續偏離給定值，則這兩項符號相同，而當被控量向給定值方向變化時，則這兩項的符號相反。

　　由于這一性質，當被控量接近給定值的時候，反號的比例作用阻礙了積分作用，因而避免了積分超調以及隨之帶來的振蕩，這顯然是有利于控制的。但如果被控量遠未接近給定值，僅剛開始向給定值變化時，由于比例和積分反向，將會減慢控制過程。

　　為了加快開始的動態過程，我們可以設定一個偏差范圍v，當偏差|e(t)|< β時，即被控量接近給定值時，就按正常規律調節，而當|e(t)|>= β時，則不管比例作用為正或為負，都使它向有利于接近給定值的方向調整，即取其值為|e(t)-e(t-1)|，其符號與積分項一致。利用這樣的算法，可以加快控制的動態過程。

　　(3) PID增量算法的飽和作用及其抑制

　　在PID增量算法中，由于執行元件本身是機械或物理的積分儲存單元，如果給定值發生突變時，由算法的比例部分和微分部分計算出的控制增量可能比較大，如果該值超過了執行元件所允許的最大限度，那么實際上執行的控制增量將時受到限制時的值，多余的部分將丟失，將使系統的動態過程變長，因此，需要采取一定的措施改善這種情況。

　　糾正這種缺陷的方法是采用積累補償法，當超出執行機構的執行能力時，將其多余部分積累起來，而一旦可能時，再補充執行。

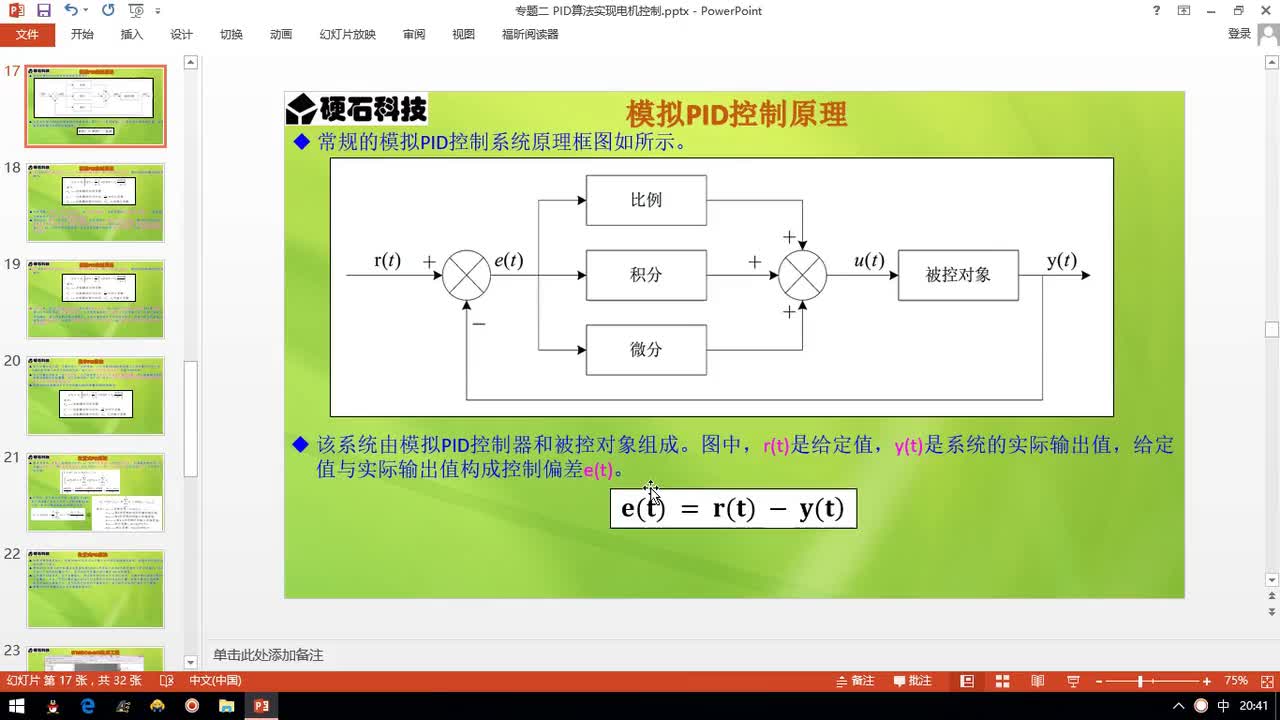
　　數字PID控制算法

　　首先，將連續的系統離散化。

　　計算機控制是一種采樣控制，它只能根據采樣時刻的偏差值計算控制量，因此，連續PID控制算法不能直接使用，需要采用離散化的方法。在計算機PID控制中，使用的是數字PID控制器。

　　采樣周期T為1ms，采用Z變換對G(S)進行離散化，離散化后的被控對象為：

　　Transfer function:

　　0.06684 z^2 - 0.1322 z + 0.06538

　　z^3 - 2.222 z^2 + 1.445 z - 0.2229

　　可得系統的差分方程：

　　y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3;

　　num =[0 0.0668 -0.1322 0.0654]

　　den =[1.0000 -2.2219 1.4448 -0.2229]

　　在輸入信號為單位階躍信號時，運行附錄2的數字PID程序，可得系統的響應如下：

?

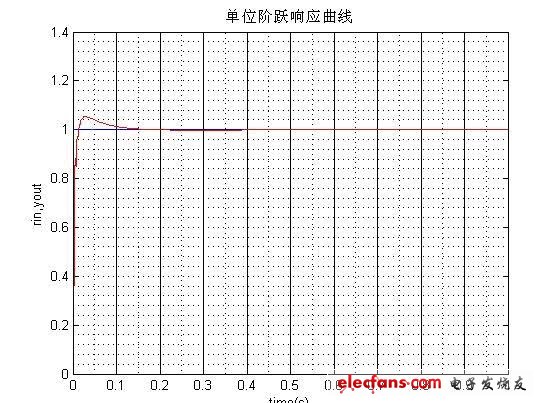
　　在PID參數：kp=10;ki=3000;kd=0; 調節時間0.15s<0.2s; 無穩態誤差, 超調量4%>2%。其中超調量過大不滿足系統的設計要求。

　　利用Matlab /Simulink軟件,構建了電機控制系統的速度仿真模型。通過仿真結果可以看出系統能平穩運行,具有較好的靜、動態特性。在此仿真模型基礎上,可以十分便捷地實現進行參數選擇、調整及仿真。因此,可以從整體角度出發對伺服系統整體參數的優化和調整進行研究。也為實際伺服系統的設計和調試提供了新的思路