四、卡諾圖化簡邏輯函數
1.幾個定義
蘊涵項:在函數的“與-或”表達式中,每個“與”項被稱為該函數的蘊涵項(Implicant)。
顯然,在函數卡諾圖中,任何一個1方格所對應的最小項或者卡諾圈中的2m個1方格所對應的“與”項都是函數的蘊涵項。
質蘊涵項:若函數的一個蘊涵項不是該函數中其他蘊涵項的子集,則此蘊涵項稱為質蘊涵項(PrimeImplicant),簡稱為質項。
顯然,在函數卡諾圖中,按照最小項合并規律,如果某個卡諾圈不可能被其他更大的卡諾圈包含,那么,該卡諾圈所對應的“與”項為質蘊涵項。
必要質蘊涵項:若函數的一個質蘊涵項包含有不被函數的其他任何質蘊涵項所包含的最小項,則此質蘊涵項被稱為必要質蘊涵項(EssentialPrimeImplicant),簡稱為必要質項。
在函數卡諾圖中,若某個卡諾圈包含了不可能被任何其他卡諾圈包含的1方格,那么,該卡諾圈所對應的“與”項為必要質蘊涵項。
2.求函數最簡“與-或”表達式
(1)一般步驟:
第一步:作出函數的卡諾圖。
第二步:在卡諾圖上圈出函數的全部質蘊涵項。按照卡諾圖上最小項的合并規律,對函數F卡諾圖中的1方格畫卡諾圈。為了圈出全部質蘊涵項,畫卡諾圈時在滿足合并規律的前題下應盡可能大,若卡諾圈不可能被更大的卡諾圈包圍,則對應的“與”項為質蘊涵項。
第三步:從全部質蘊涵項中找出所有必要質蘊涵項。在卡諾圖上只被一個卡諾圈包圍的最小項被稱為必要最小項,包含必要最小項的質蘊涵項即必要質蘊涵項。為了保證所得結果無一遺漏地覆蓋函數的所有最小項,函數表達式中必須包含所有必要質蘊涵項。
第四步:求出函數的最簡質蘊涵項集。若函數的所有必要質蘊涵項尚不能覆蓋卡諾圖上的所有1方格,則從剩余質蘊涵項中找出最簡的所需質蘊涵項,使它和必要質蘊涵項一起構成函數的最小覆蓋。
(2)舉例
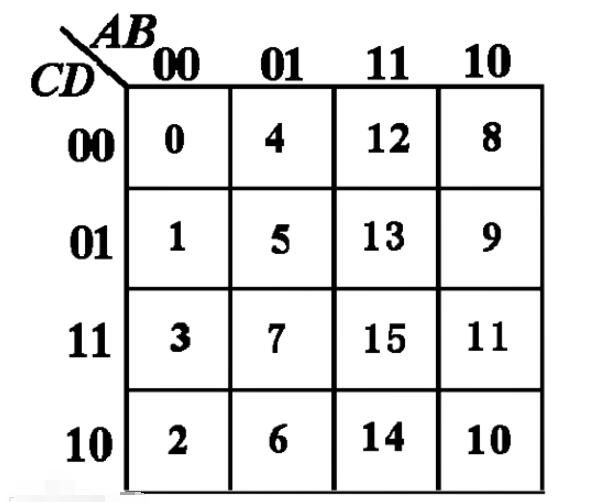
例1用卡諾圖化簡邏輯函數F(A,B,C,D)=∑m(0,3,5,6,7,10,11,13,15)。
解根據卡諾圖化簡的步驟,該題化簡過程如下:
該題中,5個必要質蘊涵項已將函數的全部最小項覆蓋,故將各卡諾圈對應的與項相或即可得到函數F的最簡“與-或”表達式為
F(A,B,C,D)=A·B·C·D+ABC+ABC+BD+CD
例2用卡諾圖化簡邏輯函數F(A,B,C,D)=∑m(2,3,6,7,8,10,12)。
解根據卡諾圖化簡的步驟,該題化簡過程如下:
由圖可知,該函數包含兩個必要質蘊涵項,即AC和AC·D。在選取必要質蘊涵項之后,尚有最小項m10未被覆蓋。為了覆蓋最小項m10,可選質蘊涵項BCD或者AB·D,由于這兩個質蘊涵項均由3個變量組成,故可任選其中之一作為所需質蘊涵項,即F的最簡質蘊涵項集可為
{AC,AC·D,BCD}或者{AC,AC·D,AB·D}
因而,可求得函數F的最簡“與-或”表達式為
F(A,B,C,D)=AC+AC·D+BCD或者F(A,B,C,D)=AC+AC·D+AB·D
這里,函數F的最簡“與-或”式有兩個,其復雜程度相同。由此可見,一個函數的最簡“與-或”表達式不一定是唯一的!
歸納起來,卡諾圖化簡的原則是:
☆在覆蓋函數中的所有最小項的前提下,卡諾圈的個數達到最少。
☆在滿足合并規律的前題下卡諾圈應盡可能大。
☆根據合并的需要,每個最小項可以被多個卡諾圈包圍。
3.求函數的最簡“或-與”表達式
當需要求一個函數的最簡“或-與”表達式時,可采用“兩次取反法”。
具體如下:
☆先求出函數F的反函數F的最簡“與-或”表達(合并卡諾圖上的0方格);
☆然后對F的最簡“與-或”表達式取反,從而得到函數F的最簡“或-與”表達式。
例如,用卡諾圖求邏輯函數F(A,B,C,D)=∑m(3,4,6,7,11,12,13,14,15)的最簡“或-與”表達式。
解首先畫出函數F的卡諾圖如圖2.13所示。
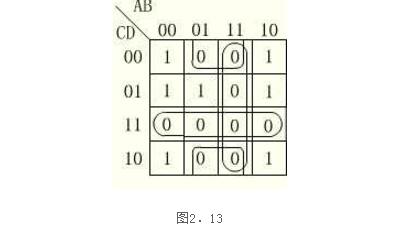
圖中,F的0方格即反函數F的1方格,它們代表F的各個最小項,將全部0方格合并就可得到反函數F的最簡“與-或”表達式
F(A,B,C,D)=AB+CD+BD
再對上述函數式兩邊取反,即可求得函數的最簡“或-與”表達式
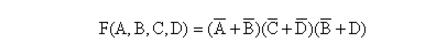
卡諾圖化簡邏輯函數具有方便、直觀、容易掌握等優點。但依然帶有試湊性。尤其當變量個數大于6時,畫圖以及對圖形的識別都變得相當復雜。
 電子發燒友App
電子發燒友App


























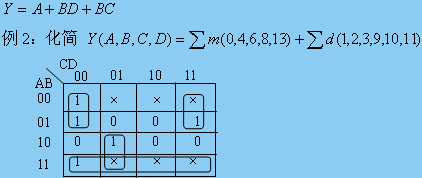










評論