次算法的缺點是運(yùn)行速度慢，但是對圖片的還原效果還是比較顯著的。

其他白平衡算法 鏡面法（PerfectReflectorModel）

根據(jù)圖像形成理論，對于純白色的反射面而言，無論光源是什么顏色，最終反射后的顏色總能完全表現(xiàn)出光源的顏色。如果景物中有純白的部分，那么就可以直接從這些像素中提取出光源信息?；谶@種思想的方法都被稱為是鏡面法。

與灰色世界法類似的，鏡面法也有多種調(diào)整方式。在本文中著重介紹兩種。

第一種方法較為基本也較為簡便。這種方法假設(shè)圖片中一定有純白色面存在，那么在經(jīng)典光源下，圖片中所有像素點三個信道的最大值都應(yīng)該等于255，或者是一個給定的純白色的值。在任何其他的光源下，圖片純白色點的像素值就會小于經(jīng)典光源下的純白色，并且這些點將代表整幅圖片中最亮的點。那么只要將各信道的值按比例規(guī)一化到最大值（純白色）就可以獲得在經(jīng)典光源下的圖片了。

假設(shè)經(jīng)典的白色表達(dá)形式可以用來表示。下標(biāo)i表示信道，上標(biāo)c表示經(jīng)典光源。假設(shè)RGB響應(yīng)的最值為，下標(biāo)i表示信道，上標(biāo)U表示未知光源。那么歸一化率的計算式為如下式所示：

根據(jù)光源轉(zhuǎn)換理論，從未知光源到經(jīng)典光源下圖片表達(dá)式的轉(zhuǎn)換同樣可以用下式定義：

其計算過程如下：

?

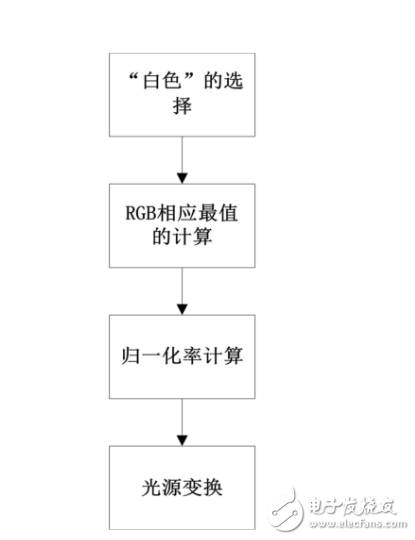
當(dāng)選擇（255，255，255）為白色值的時候只需把每個信道的像素值拉伸到最大值即可。這種鏡面法最為簡單，在有效性方面的表現(xiàn)也不錯。

第二鏡面法算法在第一步的基礎(chǔ)上改進(jìn)了對于白色點的定義。它不是將白色定義為各信道值最大的點。而是將滿足某個條件的點都定義為白色點，通過計算這些點的平均色溫，得到對于未知光源的估計值。這類算法首先將對于白色的定義形式轉(zhuǎn)換到了YCbCr空間：

在YCbCr空間中，Y是灰度，表示圖像的亮度，Cb和Cr是色度的藍(lán)色和紅色分量，代表圖像的色差。由于鏡面是圖像中亮度最大的部分，那么Y值最大的點就可以很好的代表圖像中的鏡面。

第二步就是在轉(zhuǎn)換完的空間中尋找到可以代表鏡面的點。在Y較小時，Cb和Cr較小的像素表現(xiàn)為接近白色的灰度值；而在Y較大時，Cb和Cr較大的像素仍可以認(rèn)為是白色物體受到光源污染得到的。因此我國的白平衡研究學(xué)者提出了下列約束條件：

由算法決定，不同鏡面算法的值不同。 在選出了合適的白色點之后，下一步就是要估計色溫，根據(jù)計算的色溫來還原已知光源下的圖片。色溫估計的計算式如下式所示： 其中下標(biāo)X標(biāo)示信道，在這種算法中X=Y、Cb、Cr。

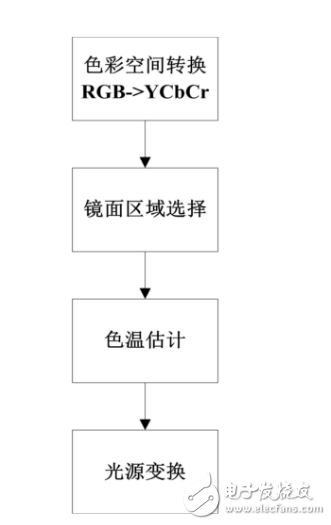
進(jìn)行色溫估計之后，利用光源轉(zhuǎn)換式可以獲得如下圖所示的計算過程：

?

音階映射法（gamutmappingmodel）

音階映射法采用了與前幾種方法完全不同的思路，是第一個很好的描述了圖片統(tǒng)計特性的算法，由Forsyth在1990年首次提出。此方法的第一步是建造一個所有可能的R、G、B值得集合，這些值是在經(jīng)典光源下拍攝所有現(xiàn)實世界可能出現(xiàn)的反射面獲得的。這個集合是一個凸多面體，因此可使用其頂點來表征。在第二步中，使用相似的方法，將圖片中所有出現(xiàn)的R、G、B值繪成一個凸多面體。第三步是將這兩個凸多面體相互映射從而獲得對角變換矩陣。根據(jù)映射得來的變換矩陣一般不是唯一的，而是一個由許多矩陣組成的集合。所以第四步就是從這個集合中挑選出最終的變換矩陣。

音階映射法的主要優(yōu)點在于對于其應(yīng)用環(huán)境沒有特別的限制，因此其平均表現(xiàn)水平要高于灰色世界法和完美反射法。其不足之處主要有三：

第一，要獲得在經(jīng)典光源下所有可能出現(xiàn)的R、G、B值集合非常困難，一般只能獲得近似集合。

第二，映射兩個三維集合的計算量比較大。

第三，獲得的變換矩陣是一個集合，沒有有效的方法獲得最優(yōu)解。 1996年Finlayson提出透視色彩法，在音階映射法的基礎(chǔ)上作了兩點改進(jìn)。第一，這種方法使用了色度空間（r，g）=（R/（R+B+G），G/（R+B+G））；第二，通過考慮可能出現(xiàn)的光源值來進(jìn)一步縮小得到的變換矩陣集合。使用色度空間之后，參數(shù)集合從三維降為兩維，降低了運(yùn)算復(fù)雜度?？紤]可能出現(xiàn)的光源以后縮小了目標(biāo)變換矩陣的范圍，使得最后得到的結(jié)果更接近最優(yōu)解。 透視色彩法的主要缺陷在于光源集合是一個非凸集合，也就說它無法僅僅使用頂點來精確表征。這樣就加大了運(yùn)算難度。

Barnard采用的方法是將其近似認(rèn)為一個凸集合，這樣就不需要增加額外的計算了，但是對最后變換矩陣集合的準(zhǔn)確獲得造成了一定負(fù)面影響。

接下來將對音階圖法的基本計算方法作一個闡述。所使用的色度空間為改進(jìn)后的二維色度空間（r，g）=（R/（R+B+G），G/（R+B+G））。

第一步為構(gòu)造色集合圖；第二步與第三步，構(gòu)造待測圖片的色集合圖并將其映射到測試色集合圖中。 經(jīng)過映射以后未知光源的圖片就與經(jīng)典光源下的可能圖像建立了映射關(guān)系。通常，建立的映射關(guān)系不是唯一的，而是一個集合，這樣就需要對這個集合中所有的映射關(guān)系進(jìn)行篩選從而獲得最佳結(jié)果。選擇的過程必須要建立額外的假設(shè)，因此不是唯一的。

色相關(guān)法（colorbycorrelationmodel）

Finlayson提出了色相關(guān)法作為對于透視色彩法的改進(jìn)。色相關(guān)法的實質(zhì)就是將色彩空間離散化，從而進(jìn)一步降低計算復(fù)雜度。色相關(guān)法的基本思想是預(yù)先計算一個矩陣，這個矩陣描述了不用光源與特定圖像色彩出現(xiàn)之間的相關(guān)度。

矩陣的每一行對應(yīng)于一個不同的訓(xùn)練光源，每一列為可能出現(xiàn)的色彩值，這些色彩值是通過離散化染色空間（r，g）獲得的。行和列可以任意排列而不影響此方法的有效性。矩陣元素A（i，j）的含義為：在光源i之下拍攝的圖片中出現(xiàn)色彩j。

色相關(guān)法中提出了兩種定義矩陣元素A（i，j）的方法。在第一種方法中，A（i，j）只能取0或1。取0表示色彩j不可能出現(xiàn)在光源i之下，取1表示色彩j可能出現(xiàn)在光源i之下。在第二種方法中，A（i，j）可以去0到1之間的任何一個值，代表色彩i出現(xiàn)在光源j之下的概率。在計算完相關(guān)矩陣之后，使用類似的方法將目標(biāo)圖片的色彩空間離散化，形成一個相關(guān)矢量，與相關(guān)矩陣相乘以獲得這個未知光源下的圖象與各個已知光源的相關(guān)度。選取相關(guān)度最大的

一個或幾個已知光源對未知光源特性進(jìn)行估計，求得未知光源特性。色相關(guān)法的好處在于，在充分考慮到圖像統(tǒng)計特性的前提下進(jìn)一步降低了計算復(fù)雜度。但是其不足也是明顯的。首先，與透視色彩法一樣，對于所有可能光源的估計是近似的，不完全的，可能影響到最后的估計結(jié)果。其次，離散化色彩空間的過程中丟失了許多色彩信息，在一些情況下，可能使相關(guān)矩陣和向量相乘后的結(jié)果為零向量。

以下將對色相關(guān)的計算步驟進(jìn)行簡要介紹： 第一步，建立相關(guān)矩陣，其過程：（a）找出在參考光源下的彩色圖像的色度；（b）計算出每個色彩在參考光源下的出現(xiàn)概率；（c）將b所計算出的概率加入色相關(guān)矩陣M。

可以看到（a）中所示的色度集合是離散的，因為色相關(guān)矩陣中的各種顏色分布也是離散的。（c）中相關(guān)矩陣的每一列代表不同的光源，在這一列中的每一個值代表了對應(yīng)的色彩區(qū)域出現(xiàn)的概率。

第二步是相關(guān)的過程。在進(jìn)行相關(guān)之前需要先構(gòu)造圖像向量，圖像向量的每一個元素值代表對應(yīng)的色彩區(qū)間是否出現(xiàn)在給定的需要進(jìn)行白平衡處理的圖片中。

接著就是相關(guān)過程了，相關(guān)矩陣與特征向量的相關(guān)過程可以簡要表示：（a）從圖像色度集合中求出圖像向量；（b）將圖像數(shù)據(jù)與可能的光源進(jìn)行相關(guān)；（c）選擇一個可能的光源。

第三步就是最佳光源的選取。最佳光源的選取有多種方法，包括最大相關(guān)值法：尋找所有相關(guān)向量中最大的元素；最大相關(guān)值平均法：將相關(guān)向量里最大的幾個值所對應(yīng)的光源色彩進(jìn)行平均，然后求出最佳光源；等等。

神經(jīng)網(wǎng)絡(luò)法（NeuralNetworkApproachtoColourConstancy）

神經(jīng)網(wǎng)絡(luò)法是處理視角比較獨(dú)特的一種白平衡算法。該方法同樣對染色空間（r，g）進(jìn)行了離散化處理，并將其與神經(jīng)網(wǎng)略結(jié)構(gòu)相聯(lián)系。目前提出的神經(jīng)網(wǎng)絡(luò)白平衡算法使用了3層結(jié)構(gòu)，輸入層有X000個節(jié)點，第一個隱藏層有X00個節(jié)點，第二個隱藏層有X0個節(jié)點，輸出層有2個節(jié)點。輸入層代表離散化的染色空間（r，g），每一個節(jié)點的輸入可取0或1，表示某個色彩值（ri，gi）是否在圖像中出現(xiàn)。輸出層表征了光源特性。上層為下層值得加權(quán)和。通過輸入不同的圖片，可以訓(xùn)練神經(jīng)網(wǎng)絡(luò)的權(quán)值，以獲得滿意的結(jié)果。

輸入神經(jīng)元有多個，輸出神經(jīng)元為兩個。神經(jīng)網(wǎng)絡(luò)的輸出描述了未知光源特性，輸入則代表了圖像的色彩特性。 對于各層結(jié)點數(shù)為多少時處理效果最優(yōu)這個問題，目前還沒有辦法在理論上進(jìn)行驗證。試驗經(jīng)驗表明，在一定的范圍內(nèi)，結(jié)點數(shù)的多少不影響處理的最終效果。但這也同時表明了，神經(jīng)網(wǎng)絡(luò)發(fā)的處理效果優(yōu)化存在一定難度。