摘要：在銀行金融界及非金融界，越來越多地用到了DES 算法， DES 全稱為Data Encryption Standard即數據加密算法。下面來說說DES算法的應用誤區及安全性分析。

　　DES算法詳述

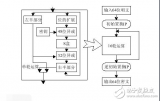
　　DES算法把64位的明文輸入塊變為64位的密文輸出塊，它所使用的密鑰也是64位，整個算法的主流程圖如下：

　　其功能是把輸入的64位數據塊按位重新組合，并把輸出分為L0、R0兩部分，每部分各長32位，其置換規則見下表：

　　58，50，12，34，26，18，10，2，60，52，44，36，28，20，12，4，

　　62，54，46，38，30，22，14，6，64，56，48，40，32，24，16，8，

　　57，49，41，33，25，17， 9，1，59，51，43，35，27，19，11，3，

　　61，53，45，37，29，21，13，5，63，55，47，39，31，23，15，7，

　　即將輸入的第58位換到第一位，第50位換到第2位，。。。，依此類推，最后一位是原來的第7位。L0、R0則是換位輸出后的兩部分，L0是輸出的左32位，R0 是右32位，例：設置換前的輸入值為D1D2D3.。。。。.D64，則經過初始置換后的結果為：L0=D58D50.。.D8；R0=D57D49.。.D7。

　　經過26次迭代運算后。得到L16、R16，將此作為輸入，進行逆置換，即得到密文輸出。逆置換正好是初始置的逆運算，例如，第1位經過初始置換后，處于第40位，而通過逆置換，又將第40位換回到第1位，其逆置換規則如下表所示：

　　40，8，48，16，56，24，64，32，39，7，47，15，55，23，63，31，

　　38，6，46，14，54，22，62，30，37，5，45，13，53，21，61，29，

　　36，4，44，12，52，20，60，28，35，3，43，11，51，19，59，27，

　　34，2，42，10，50，18，58 26，33，1，41， 9，49，17，57，25，

　　放大換位表

　　32， 1， 2， 3， 4， 5， 4， 5， 6， 7， 8， 9， 8， 9， 10，11，

　　12，13，12，13，14，15，16，17，16，17，18，19，20，21，20，21，

　　22，23，24，25，24，25，26，27，28，29，28，29，30，31，32， 1，

　　單純換位表

　　16，7，20，21，29，12，28，17， 1，15，23，26， 5，18，31，10，

　　2，8，24，14，32，27， 3， 9，19，13，30， 6，22，11， 4，25，

　　在f（Ri，Ki）算法描述圖中，S1，S2.。.S8為選擇函數，其功能是把6bit數據變為4bit數據。下面給出選擇函數Si（i=1，2.。。。。.8）的功能表：

　　選擇函數Si

　　S1：

　　14，4，13，1，2，15，11，8，3，10，6，12，5，9，0，7，

　　0，15，7，4，14，2，13，1，10，6，12，11，9，5，3，8，

　　4，1，14，8，13，6，2，11，15，12，9，7，3，10，5，0，

　　15，12，8，2，4，9，1，7，5，11，3，14，10，0，6，13，

　　S2：

　　15，1，8，14，6，11，3，4，9，7，2，13，12，0，5，10，

　　3，13，4，7，15，2，8，14，12，0，1，10，6，9，11，5，

　　0，14，7，11，10，4，13，1，5，8，12，6，9，3，2，15，

　　13，8，10，1，3，15，4，2，11，6，7，12，0，5，14，9，

　　S3：

　　10，0，9，14，6，3，15，5，1，13，12，7，11，4，2，8，

　　13，7，0，9，3，4，6，10，2，8，5，14，12，11，15，1，

　　13，6，4，9，8，15，3，0，11，1，2，12，5，10，14，7，

　　1，10，13，0，6，9，8，7，4，15，14，3，11，5，2，12，

　　S4：

　　7，13，14，3，0，6，9，10，1，2，8，5，11，12，4，15，

　　13，8，11，5，6，15，0，3，4，7，2，12，1，10，14，9，

　　10，6，9，0，12，11，7，13，15，1，3，14，5，2，8，4，

　　3，15，0，6，10，1，13，8，9，4，5，11，12，7，2，14，

　　S5：

　　2，12，4，1，7，10，11，6，8，5，3，15，13，0，14，9，

　　14，11，2，12，4，7，13，1，5，0，15，10，3，9，8，6，

　　4，2，1，11，10，13，7，8，15，9，12，5，6，3，0，14，

　　11，8，12，7，1，14，2，13，6，15，0，9，10，4，5，3，

　　S6：

　　12，1，10，15，9，2，6，8，0，13，3，4，14，7，5，11，

　　10，15，4，2，7，12，9，5，6，1，13，14，0，11，3，8，

　　9，14，15，5，2，8，12，3，7，0，4，10，1，13，11，6，

　　4，3，2，12，9，5，15，10，11，14，1，7，6，0，8，13，

　　S7：

　　4，11，2，14，15，0，8，13，3，12，9，7，5，10，6，1，

　　13，0，11，7，4，9，1，10，14，3，5，12，2，15，8，6，

　　1，4，11，13，12，3，7，14，10，15，6，8，0，5，9，2，

　　6，11，13，8，1，4，10，7，9，5，0，15，14，2，3，12，

　　S8：

　　13，2，8，4，6，15，11，1，10，9，3，14，5，0，12，7，

　　1，15，13，8，10，3，7，4，12，5，6，11，0，14，9，2，

　　7，11，4，1，9，12，14，2，0，6，10，13，15，3，5，8，

　　2，1，14，7，4，10，8，13，15，12，9，0，3，5，6，11，

　　在此以S1為例說明其功能，我們可以看到：在S1***有4行數據，命名為0，1、2、3行；每行有16列，命名為0、1、2、3，。。。。。。，14、15列。

　　現設輸入為： D＝D1D2D3D4D5D6

　　令：列＝D2D3D4D5

　　行＝D1D6

　　然后在S1表中查得對應的數，以4位二進制表示，此即為選擇函數S1的輸出。下面給出子密鑰Ki（48bit）的生成算法

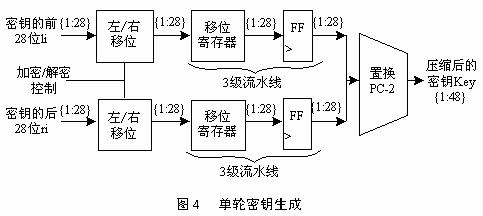
　　從子密鑰Ki的生成算法描述圖中我們可以看到：初始Key值為64位，但DES算法規定，其中第8、16、。。。。。.64位是奇偶校驗位，不參與DES運算。故Key 實際可用位數便只有56位。即：經過縮小選擇換位表1的變換后，Key 的位數由64 位變成了56位，此56位分為C0、D0兩部分，各28位，然后分別進行第1次循環左移，得到C1、D1，將C1（28位）、D1（28位）合并得到56位，再經過縮小選擇換位2，從而便得到了密鑰K0（48位）。依此類推，便可得到K1、K2、。。。。。。、K15，不過需要注意的是，16次循環左移對應的左移位數要依據下述規則進行：

　　循環左移位數

　　1，1，2，2，2，2，2，2，1，2，2，2，2，2，2，1

　　以上介紹了DES算法的加密過程。DES算法的解密過程是一樣的，區別僅僅在于第一次迭代時用子密鑰K15，第二次K14、。。。。。。，最后一次用K0，算法本身并沒有任何變化。

　　DES算法的安全性

　　自分組密碼（DES算法）1977年首次公諸于世以來，引起了學術界和企業界的廣泛重視。學術界對DES密碼進行了深入的研究，圍繞它的安全性和破譯方法展開了激烈的爭論，在一定意義上對密碼學的理論研究也起了推動作用。同時人們也一直對DES的安全性持懷疑態度，對密鑰的長度、迭代次數及S盒的設計眾說紛紜

　　1.對稱分組密碼算法的問題

　　DES是對稱的分組密碼算法。對稱的分組密碼算法最主要的問題是：由于加解密雙方都要使用相同的密鑰，因此在發送、接收數據之前，必須完成密鑰的分發。因而，密鑰的分發便成了該加密體系中的最薄弱、風險最大的環節，各種基本的手段均很難保障安全地完成此項工作，從而使密鑰更新的周期加長，給他人破譯密鑰提供了機會。實際上這與傳統的保密方法差別不大。在歷史戰爭中，破獲他國情報的紀錄不外是兩種方式：一種是在敵方更換“密碼本”的過程中截獲對方密碼本;另一種是敵人密鑰變動周期太長，被長期跟蹤，找出規律從而被破獲。在對稱算法中，盡管由于密鑰強度增強，跟蹤找出規律破獲密鑰的機會大大減小了，但密鑰分發的困難問題幾乎無法解決。如，設有n方參與通信，若n方都采用同一個對稱密鑰，一旦密鑰被破解，整個體系就會***;若采用不同的對稱密鑰則需n（n-1）個密鑰，密鑰數與參與通信人數的平方數成正比，這便使大系統密鑰的管理幾乎成為不可能。

　　2.DES算法的弱密鑰

　　由于算法各輪的子密鑰是通過改變初始密鑰這種方式得到的，因此有些初始密鑰成了弱密鑰（weakkey）。初始密鑰分成兩部分，每部分各自獨立的移動。如果每一部分的所有位都是0或1，那么算法的任意一個周期的密鑰都是相同的。當密鑰是全1、全0、或者一半全1、一半全0時，會發生這種情況。下面以十六進制編碼的方式給出了四種弱密鑰。

　　另外，還有一些密鑰對明文加密成相同的密文。換句話說，密鑰對里的一個密鑰能解密另外一個。

　　密鑰加密的信息。這是由DES產生子密鑰（subkey）的方式決定的。這些密鑰只產生2個不同的子密鑰，算法中每個這樣的子密鑰都使用了8次。這樣的子密鑰叫半弱密鑰（semiweakkey），下表以十六進制編碼方式給出它們。

　　另外，也只有產生4個子密鑰的密鑰，每個這樣的子密鑰在算法中使用了4次。下面給出他們的十六進制編碼形式

　　雖然DES有弱密鑰，但這張64個密鑰的密鑰表相對于總數位72，057，594，037，927，936個可能密鑰的密鑰集只是個零頭，如果隨機的選擇密鑰，選中這些弱密鑰的可能性可以忽略。而且我們可以在選擇密鑰時進行檢查，以防止產生弱密鑰

　　3.密鑰的長度

　　密鑰僅有56位二進制未免太短，多密碼學專家力薦使用更長的密鑰，理由是窮舉攻擊的可能性。設已知一段密碼文C及與它對應的明碼文M，用一切可能的密鑰K加密M，直到得到E（M）=C，這時所用的密鑰K即為要破譯的密碼的密鑰。窮舉法的時間復雜性是T=O（n），空間復雜性是S=O（1）。對于DES密碼，n=256≈7×106，即使使用每秒種可以計算一百萬個密鑰的大型計算機，也需要算106天才能求得所使用的密鑰，因此看來是很安全的。

　　但是密碼專家Diffie和Hellman指出，如果設計一種一微秒可以核算一個密鑰的超大規模集成片，那么它在一天內可以核算8.64×1010個密鑰。如果由一個百萬個這樣的集成片構成專用機，那么它可以在不到一天的時間內用窮舉法破譯DES密碼。他們當時（1977年）估計：這種專用機的造價約為兩千萬美元。如果在五年內分期償還，平均每天約需付一萬美元。由于用窮舉法破譯平均只需要計算半個密鑰空間，因此獲得解的平均時間為半天。這樣，破譯每個DES密碼的花銷只是五千美元。后來，Diffie在1981年又修改了他們的估計，認為以1980年的技術而論，用造價為五千萬美元的專用機破譯DES密碼平均要花兩天時間。但是他與Hellman都預計：1990年時，破譯DES密碼的專用機的造價將大幅度下降。

　　同時，DES的硬件實現方法逐步接近Diffie和Hellman的專用機所要求每秒百萬次的速度。在1993年，MuchaelWiener設計了一個一百萬美元的機器，它能在平均3.5小時內，完成DES的窮舉攻擊，到1990年時，DES是完全不安全的。

　　4.迭代次數

　　根據目前的計算技術和DES的分析情況，16-圈DES仍然是安全的，但提醒使用者不要使用低于16-圈的DES，特別是10-圈以下的DES，Bihan和Shamir的差分密鑰分析同樣也闡述了這一點：對于低于16輪的任意DES的已知明文攻擊要比窮舉攻擊有效，但當算法恰好有16輪時，只有窮舉攻擊最有效。

　　5.S盒和P盒的設計

　　實現替代函數Si所用的S盒的設計原理尚未公開，其中可能留有隱患。更有人擔心DES算法中有“陷阱”，知道秘密的人可以很容易地進行密文解密。目前人們仍然不知道DES中是否存在陷門。所謂陷門，通俗地講，就是在算法的設計中設計者留了一個后門，知道某一秘密的人可進入這一后門獲得使用該算法的用戶的秘密密鑰.DES的設計準則除了極少數被公布外，其余的仍然是保密的。圍繞S盒人們討論了一系列問題包括設計準則和構造等。在差分分析公開后，IBM公布了S盒和P盒的設計準則。

　　5.1 S盒的設計準則

　　1）每個S盒均為6位輸入，4位輸出。（這是在1974年的技術條件下，單個芯片所能容納的最大尺寸。）

　　2）沒有一個S盒的輸出位是接近輸入位的線性函數。

　　3）如果將輸入位的最左、最右端的位固定，變化中間的4位，每個可能的4位輸出只得到一次.4）如果S盒的兩個輸入僅有1位的差異，則其輸出必須至少有2位不同.5）如果S盒的兩個輸入僅有中間2位不同，則其輸出必須至少有2位不同。

　　6）如果S盒的兩個輸入前2位不同，后兩位已知，則其輸出必不同。

　　7）對于輸入之間的任何非零的6位差分，32對中至多有8對顯示出的差分導致了相同的輸出差分。

　　5.2 P盒的設計準則

　　1）在第i輪S盒的4位輸出中，2位將影響S盒第i+1輪的中間位，其余2位將影響最后位;2）每個S盒的4位輸出影響6個不同的S盒，但沒有一個影響同一個S盒;

　　3）如果一個S盒的4位輸出影響另一個S盒的中間1位，那么后一個的輸出位不會影響前一個S盒的中間1位。

　　在今天看來產生S盒很容易，但在70年代初，這是一個很復雜的工作.Tuchman曾經引述說，他們當時將計算機程序運行幾個月來產生S盒。在對DES密碼進行鑒定的期間，美國國家保密局和計算機科學技術學會組織各界專家研究了DES密碼體制的安全性問題，討論了破譯DES密碼體制的一切可能途徑。盡管有些專家和學者對它的安全性仍持懷疑態度，但官方卻得出了十分樂觀的結論。他們宣布：“沒有任何可以破譯DES密碼體制的系統分析法。若使用窮舉法，則在1990年以前基本上不可能產生出每天能破譯一個DES密鑰的專用計算機。即使屆時能制造出這樣的專用機，它的破譯成功率也只會在0.1到0.2之間，而且造價可能高達幾千萬美元

　　DES算法的漏洞

　　由DES算法我們可以看到：DES算法中只用到64位密鑰中的其中56位，而第8、16、24、……64位8個位并未參與DES運算。這一點，向我們提出了一個應用上的要求，即DES的安全性是基于除了8，16，24，……64位外的其余56位的組合變化256才得以保證的。因此，在實際應用中，我們應避開使用第8，16，24……64位作為DES密鑰的有效數據位，而使用其它的56位作為有效數據位。只有這樣，才能保證DES算法安全可靠地發揮作用。如果不了解這一點，把密鑰Key的8，16，24，……64位作為有效數據位使用，將不能保證DES加密數據的安全性，對運用DES來達到保密作用的系統將產生數據被破譯的危險，這正是DES算法在應用上的誤區，是各級技術人員、各級用戶在使用過程中應絕對避免的。

　　基于以上的問題，我們就不能用漢字作為密鑰。因為漢字由兩個字節組成，每個字節的ASCII碼都大于127，轉換成二進制就是8位，不能加奇偶校驗位，而且如果去掉第8、16、24、……64位，就會丟失密鑰，而且不同的漢字可能實際上是相同的密鑰.

　　DES算法的應用誤區

　　DES算法具有極高安全性，到目前為止，除了用窮舉搜索法對DES算法進行攻擊外，還沒有發現更有效的辦法。而56位長的密鑰的窮舉空間為256，這意味著如果一臺計算機的速度是每一秒種檢測一百萬個密鑰，則它搜索完全部密鑰就需要將近2285年的時間，可見，這是難以實現的，當然，隨著科學技術的發展，當出現超高速計算機后，我們可考慮把DES密鑰的長度再增長一些，以此來達到更高的保密程度。

　　由上述DES算法介紹我們可以看到：DES算法中只用到64位密鑰中的其中56位，而第8、16、24、。。。。。.64位8個位并未參與DES運算，這一點，向我們提出了一個應用上的要求，即DES的安全性是基于除了8，16，24，。。。。。.64位外的其余56位的組合變化256才得以保證的。因此，在實際應用中，我們應避開使用第8，16，24，。。。。。.64位作為有效數據位，而使用其它的56位作為有效數據位，才能保證DES算法安全可靠地發揮作用。如果不了解這一點，把密鑰Key的8，16，24，。。。。。 .64位作為有效數據使用，將不能保證DES加密數據的安全性，對運用DES來達到保密作用的系統產生數據被破譯的危險，這正是DES算法在應用上的誤區，是各級技術人員、各級領導在使用過程中應絕對避免的，而當今國內各金融部門及非金融部門，在運用DES工作，掌握DES工作密鑰Key的領導、主管們，極易忽略，給使用中貌似安全的系統，留下了被人攻擊、被人破譯的極大隱患。

　　DES算法應用誤區的驗證數據

　　筆者用Turbo C編寫了DES算法程序，并在PC機上對上述的DES 算法的應用誤區進行了騅，其驗證數據如下：

　　Key： 0x30 0x30 0x30 0x30.。。。。.0x30（8個字節）

　　Data： 0x31 0x31 0x31 0x31.。。。。.0x31（8個字節）

　　Mode： Encryption

　　結果：65 5e a6 28 cf 62 58 5f

　　如果把上述的Key換為8個字節的0x31，而Data和Mode均不變，則執行DES 后得到的密文完全一樣。類似地，用Key:8個0x32和用Key:8個0x33 去加密Data （8 個0x31），二者的圖文輸出也是相同的：5e c3 ac e9 53 71 3b ba

　　我們可以得到出結論：

　　Key用0x30與用0x31是一樣的；

　　Key用0x32與用0x33是一樣的，。。。。。。

　　當Key由8個0x32換成8個0x31后，貌似換成了新的Key，但由于0x30和0x31僅僅是在第8，16，24.。。。。.64有變化，而DES算法并不使用Key的第8，16，。。。。。.64位作為Key的有效數據位，故：加密出的結果是一樣的。

　　DES解密的驗證數據：

　　Key： 0x31 0x31.。。。。.0x31（8個0x31）

　　Data： 65 5e a6 28 cf 62 58 5f

　　Mode： Decryption

　　結果：0x31 0x31.。。。。.0x31（8個0x31）

　　由以上看出：DES算法加密與解密均工作正確。唯一需要避免的是：在應用中，避開使用Key的第8，16.。。。。.64位作為有效數據位，從而便避開了DES 算法在應用中的誤區。

　　避開DES算法應用誤區的具體操作

　　在DES密鑰Key的使用、管理及密鑰更換的過程中，應絕對避開DES 算法的應用誤區，即：絕對不能把Key的第8，16，24.。。。。.64位作為有效數據位，來對Key 進行管理。這一點，特別推薦給金融銀行界及非金融業界的領導及決策者們，尤其是負責管理密鑰的人，要對此點予以高度重視。有的銀行金融交易網絡，利用定期更換DES密鑰Key的辦法來進一步提高系統的安全性和可靠性，如果忽略了上述應用誤區，那么，更換新密鑰將是徒勞的，對金融交易網絡的安全運行將是十分危險的，所以更換密鑰一定要保證新Key與舊Key真正的不同，即除了第8，16，24，。。.64位外其它位數據發生了變化，請務必對此保持高度重視！