標簽　>　拉普拉斯變換

拉普拉斯變換

+關注1人關注

文章：26個瀏覽：10287次帖子：8個

全部技術資訊資料帖子視頻產(chǎn)品方案企業(yè)

拉普拉斯變換技術

拉普拉斯變換的作用及意義

拉普拉斯變換在工程數(shù)學中是一種重要的積分變換，其作用及意義主要體現(xiàn)在以下幾個方面：作用簡化求解過程：微分方程轉換為代數(shù)方程：拉普拉斯變換可以將...

2024-08-09 標簽：濾波器信號處理函數(shù) 2493 0

傅里葉變換和拉普拉斯變換的關系是什么

傅里葉變換和拉普拉斯變換是兩種重要的數(shù)學工具，常用于信號分析和系統(tǒng)理論領域。雖然它們在數(shù)學定義和應用上有所差異，但它們之間存在緊密的聯(lián)系和相互依存的關系...

2024-02-18 標簽：函數(shù)信號分析傅里葉變換 2578 0

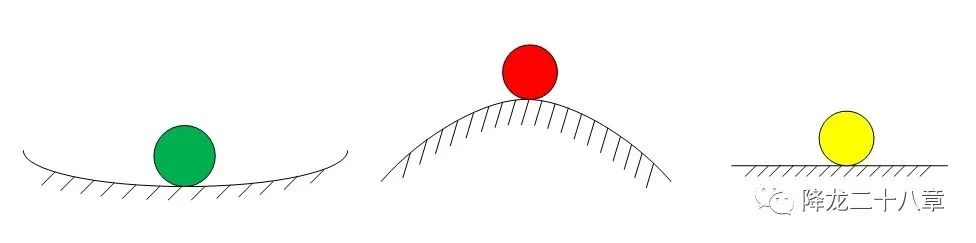
控制上是怎么描述穩(wěn)定性？如何判斷一個系統(tǒng)是否穩(wěn)定呢？

定的概念廣泛存在于各個領域，大到飛機火箭橋梁建筑，小到生活中常見的各類電子產(chǎn)品生活用品，只要涉及到“可控”的要求，一定會談到穩(wěn)定性（Stability）...

2023-12-05 標簽：電壓源 LCR 電容充放電 3359 0

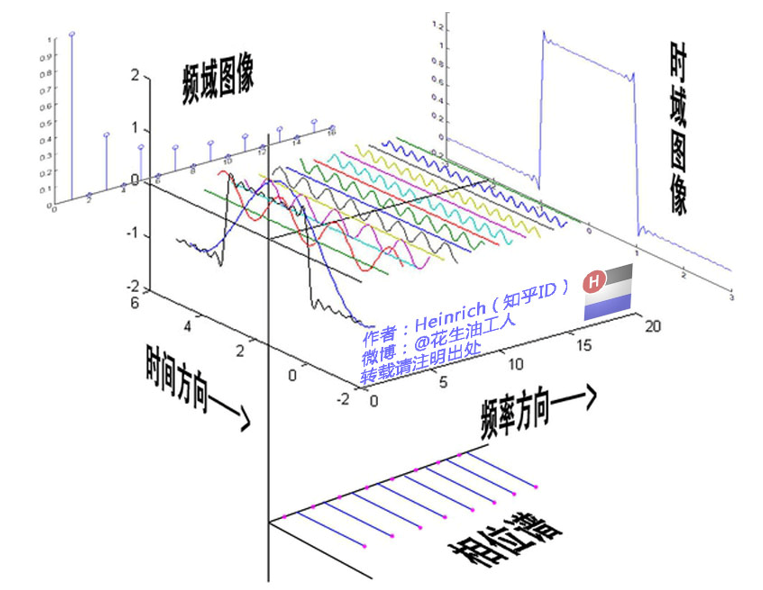
零極點的物理本質是什么？如何對系統(tǒng)產(chǎn)生影響？

每次想弄清楚零極點的物理本質是什么，如何對系統(tǒng)產(chǎn)生影響（大學信號與系統(tǒng)沒好好學)，網(wǎng)上找一下相關內(nèi)容，總能看到 ”Hs=A0/(s+a）極點為s=-...

2023-11-29 標簽：頻率響應傅里葉變換拉普拉斯變換 1695 0

電流環(huán)整定介紹

忽略前饋補償，并且反電動勢相對電流變化緩慢，可以假設看成常數(shù)，也就是等效為初始條件不為零

2023-10-25 標簽：永磁同步電機電流環(huán)反電動勢 709 0

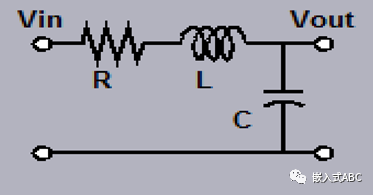
使用(s域)傳遞函數(shù)分析串聯(lián)RLC電路系統(tǒng)

線性非時變系統(tǒng)定義給我們帶來了許多數(shù)學工具，也包含卷積積分，傅里葉變換和拉普拉斯變換。

2023-10-17 標簽：串聯(lián)電路傅里葉變換拉普拉斯變換 8343 0

低通濾波器的傳遞函數(shù)簡析

濾波器的響應可以用s域傳遞函數(shù)表示；變量s來自拉普拉斯變換，代表復雜的頻率。

2023-09-19 標簽：電容器濾波器電阻器 8627 0

深入了解濾波器的原理

我們認識了音頻濾波器，講解了音頻濾波器同時具有相位調(diào)制的功能。但前文中我們略過了濾波器最重要的功能：移除頻譜中的一部分諧波從而創(chuàng)造新的聲音。但濾波器的工...

2023-07-11 標簽：電感器均衡器音頻濾波器 2019 0

電容1/sC與電感sL的由來

電容1/sC,電感sL的由來，想必很多人跟我一樣，大一大二上來就學模擬電子線路，直接給出電容可以表示為1/sC,電感可以表示sL，然后將其看成一個純粹的電阻。

2023-05-25 標簽：傅里葉變換 VCR 電容電感 2.2萬 0

為什么要進行拉普拉斯變換與傅里葉變換呢

數(shù)學變換是指數(shù)學函數(shù)從原向量空間在自身函數(shù)空間變換，或映射到另一個函數(shù)空間，或對于集合X到其自身（比如線性變換）或從X到另一個集合Y的可逆變換函數(shù)。

2022-07-23 標簽：傅里葉變換拉普拉斯變換 2811 0

如何用電路證明傅立葉變換成立？

傅立葉變換實際上有一個局限性，就是要求這個信號絕對可積，可實際上很多信號都不滿足這一條件。

2020-08-07 標簽：傅立葉拉普拉斯變換 3427 0

傅里葉變換和拉普拉斯變換的物理解釋及區(qū)別

Z變換和傅里葉變換之間有存在什么樣的關系呢？傅里葉變換的物理意義非常清晰：將通常在時域表示的信號，分解為多個正弦信號的疊加。

2019-09-29 標簽：傅里葉變換拉普拉斯變換 6312 0

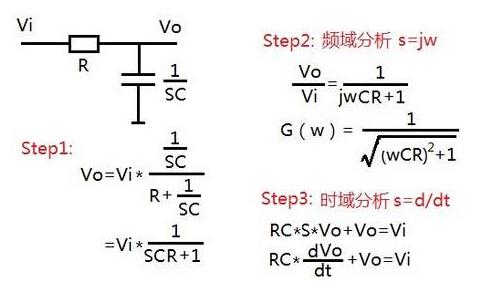
拉普拉斯變換的簡單應用

拉普拉斯變換是工程數(shù)學中常用的一種積分變換，又名拉氏變換。拉氏變換是一個線性變換，可將一個有引數(shù)實數(shù)t（t≥ 0）的函數(shù)轉換為一個引數(shù)為復數(shù)s的函數(shù)。

2018-09-17 標簽：電路設計拉普拉斯變換 1.3萬 0

RLC網(wǎng)絡直接可以利用相量分析方法給出穩(wěn)態(tài)解

這是個零狀態(tài)響應，輸入為一個余弦電壓信號：Uin = U0 cos(ωt)注意，其響應是兩個等幅度但不同頻率的余弦信號的疊加，那就是首帖的仿真結果——差拍。

2018-06-11 標簽：RLC 拉普拉斯變換 6151 0

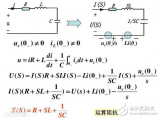
拉普拉斯變換有什么用?其物理意義是什么

拉普拉斯變換是工程數(shù)學中常用的一種積分變換，又名拉氏變換。拉氏變換是一個線性變換，可將一個有參數(shù)實數(shù)t（t≥ 0）的函數(shù)轉換為一個參數(shù)為復數(shù)s的函數(shù)。拉...

2017-12-06 標簽：拉普拉斯變換 8.3萬 0

拉普拉斯變換與傅里葉變換有什么關系嗎

一種積分變換，它來源于函數(shù)的傅里葉積分表示。積分稱為? 的傅里葉積分。拉普拉斯變換是工程數(shù)學中常用的一種積分變換，又名拉氏變換。拉氏變換是一個線性變換，...

2017-12-05 標簽：傅里葉變換拉普拉斯變換 9.1萬 2

相關話題

換一批

IOT

IOT

+關注

IoT是Internet of Things的縮寫，字面翻譯是“物體組成的因特網(wǎng)”，準確的翻譯應該為“物聯(lián)網(wǎng)”。物聯(lián)網(wǎng)（Internet of Things）又稱傳感網(wǎng)，簡要講就是互聯(lián)網(wǎng)從人向物的延伸。
海思

海思

+關注
STM32F103C8T6

STM32F103C8T6

+關注

STM32F103C8T6是一款集成電路，芯體尺寸為32位，程序存儲器容量是64KB，需要電壓2V~3.6V，工作溫度為-40°C ~ 85°C。
數(shù)字隔離

數(shù)字隔離

+關注

數(shù)字隔離技術常用于工業(yè)網(wǎng)絡環(huán)境的現(xiàn)場總線、軍用電子系統(tǒng)和航空航天電子設備中，尤其是一些應用環(huán)境比較惡劣的場合。數(shù)字隔離電路主要用于數(shù)字信號和開關量信號的傳輸。另一個重要原因是保護器件（或人）免受高電壓的危害。本文詳細介紹了數(shù)字隔離器工作原理及特點，選型及應用，各類數(shù)字隔離器件性能比較等內(nèi)容。
硬件工程師

硬件工程師

+關注

硬件工程師Hardware Engineer職位要求熟悉計算機市場行情；制定計算機組裝計劃；能夠選購組裝需要的硬件設備，并能合理配置、安裝計算機和外圍設備；安裝和配置計算機軟件系統(tǒng)；保養(yǎng)硬件和外圍設備；清晰描述出現(xiàn)的計算機軟硬件故障。
wifi模塊

wifi模塊

+關注

Wi-Fi模塊又名串口Wi-Fi模塊，屬于物聯(lián)網(wǎng)傳輸層，功能是將串口或TTL電平轉為符合Wi-Fi無線網(wǎng)絡通信標準的嵌入式模塊，內(nèi)置無線網(wǎng)絡協(xié)議IEEE802.11b.g.n協(xié)議棧以及TCP/IP協(xié)議棧。傳統(tǒng)的硬件設備嵌入Wi-Fi模塊可以直接利用Wi-Fi聯(lián)入互聯(lián)網(wǎng)，是實現(xiàn)無線智能家居、M2M等物聯(lián)網(wǎng)應用的重要組成部分。
MPU6050

MPU6050

+關注

MPU-6000（6050）為全球首例整合性6軸運動處理組件，相較于多組件方案，免除了組合陀螺儀與加速器時間軸之差的問題，減少了大量的封裝空間。
74ls74

74ls74

+關注

74LS74是雙D觸發(fā)器。功能多，可作雙穩(wěn)態(tài)、寄存器、移位寄存器、振蕩器、單穩(wěn)態(tài)、分頻計數(shù)器等功能。本章詳細介紹了74ls112的功能及原理，74ls74引腳圖及功能表，74ls112的應用等內(nèi)容。
Protues

Protues

+關注

Proteus軟件是英國Lab Center Electronics公司出版的EDA工具軟件（該軟件中國總代理為廣州風標電子技術有限公司）。它不僅具有其它EDA工具軟件的仿真功能，還能仿真單片機及外圍器件。
UHD

UHD

+關注

UHD是”超高清“的意思UHD的應用在電視機技術上最為普遍，目前已有不少廠商推出了UHD超高清電視。
STC12C5A60S2

STC12C5A60S2

+關注

在眾多的51系列單片機中，要算國內(nèi)STC 公司的1T增強系列更具有競爭力，因他不但和8051指令、管腳完全兼容，而且其片內(nèi)的具有大容量程序存儲器且是FLASH工藝的，如STC12C5A60S2單片機內(nèi)部就自帶高達60K FLASHROM，這種工藝的存儲器用戶可以用電的方式瞬間擦除、改寫。
循跡小車

循跡小車

+關注

做單片機的工程師相比都堆循跡小車有所認識，它是自動引導機器人系統(tǒng)的基本應用，那么今天小編就給大家介紹下自動自動循跡小車的原理，智能循跡小車的應用，智能循跡小車程序，循跡小車用途等知識吧！
LM2596

LM2596

+關注

LM2596是降壓型電源管理單片集成電路的開關電壓調(diào)節(jié)器，能夠輸出3A的驅動電流，同時具有很好的線性和負載調(diào)節(jié)特性。固定輸出版本有3.3V、5V、12V，可調(diào)版本可以輸出小于37V的各種電壓。
光立方

光立方

+關注

光立方是由四千多棵光藝高科技“發(fā)光樹”組成的，在2009年10月1日天安門廣場舉行的國慶聯(lián)歡晚會上面世。這是新中國成立六十周年國慶晚會最具創(chuàng)意的三大法寶之首。
光模塊

光模塊

+關注

光模塊(optical module)由光電子器件、功能電路和光接口等組成，光電子器件包括發(fā)射和接收兩部分。簡單的說，光模塊的作用就是光電轉換，發(fā)送端把電信號轉換成光信號，通過光纖傳送后，接收端再把光信號轉換成電信號。
K60

K60

+關注
STM32單片機

STM32單片機

+關注

STM32系列基于專為要求高性能、低成本、低功耗的嵌入式應用專門設計的ARM Cortex-M3內(nèi)核
Nexperia

Nexperia

+關注

Nexperia是大批量生產(chǎn)基本半導體的領先專家，這些半導體是世界上每個電子設計都需要的組件。該公司廣泛的產(chǎn)品組合包括二極管、雙極晶體管、ESD 保護器件、MOSFET、GaN FET 以及模擬和邏輯IC。
步進驅動器

步進驅動器

+關注

步進驅動器是一種將電脈沖轉化為角位移的執(zhí)行機構。當步進驅動器接收到一個脈沖信號，它就驅動步進電機按設定的方向轉動一個固定的角度（稱為“步距角”），它的旋轉是以固定的角度一步一步運行的。可以通過控制脈沖個數(shù)來控制角位移量，從而達到準確定位的目的；同時可以通過控制脈沖頻率來控制電機轉動的速度和加速度，從而達到調(diào)速和定位的目的。
CD4046

CD4046

+關注

cD4046是通用的CMOS鎖相環(huán)集成電路，其特點是電源電壓范圍寬（為3V－18V），輸入阻抗高（約100MΩ），動態(tài)功耗小，在中心頻率f0為10kHz下功耗僅為600μW，屬微功耗器件。本章主要介紹內(nèi)容有，CD4046的功能 cd4046鎖相環(huán)電路，CD4046無線發(fā)射，cd4046運用，cd4046鎖相環(huán)電路圖。
COMSOL

COMSOL

+關注

COMSOL集團是全球多物理場建模解決方案的提倡者與領導者。憑借創(chuàng)新的團隊、協(xié)作的文化、前沿的技術、出色的產(chǎn)品，這家高科技工程軟件公司正飛速發(fā)展，并有望成為行業(yè)領袖。其旗艦產(chǎn)品COMSOL Multiphysics 使工程師和科學家們可以通過模擬，賦予設計理念以生命。
加速度傳感器

加速度傳感器

+關注

加速度傳感器是一種能夠測量加速度的傳感器。通常由質量塊、阻尼器、彈性元件、敏感元件和適調(diào)電路等部分組成。
聯(lián)網(wǎng)技術

聯(lián)網(wǎng)技術

+關注
服務機器人

服務機器人

+關注

服務機器人是機器人家族中的一個年輕成員，到目前為止尚沒有一個嚴格的定義。不同國家對服務機器人的認識不同。
四軸飛行器

四軸飛行器

+關注

四軸飛行器，又稱四旋翼飛行器、四旋翼直升機，簡稱四軸、四旋翼。這四軸飛行器（Quadrotor）是一種多旋翼飛行器。四軸飛行器的四個螺旋槳都是電機直連的簡單機構，十字形的布局允許飛行器通過改變電機轉速獲得旋轉機身的力，從而調(diào)整自身姿態(tài)。具體的技術細節(jié)在“基本運動原理”中講述。
基站測試

基站測試

+關注

802.11ac與11基站測試（base station tests）在基站設備安裝完畢后，對基站設備電氣性能所進行的測量。n的區(qū)別，802.11n無線網(wǎng)卡驅動，802.11n怎么安裝。
SDK

SDK

+關注

　　SDK一般指軟件開發(fā)工具包，軟件開發(fā)工具包一般都是一些軟件工程師為特定的軟件包、軟件框架、硬件平臺、操作系統(tǒng)等建立應用軟件時的開發(fā)工具的集合。軟件開發(fā)工具廣義上指輔助開發(fā)某一類軟件的相關文檔、范例和工具的集合。
TMS320F28335

TMS320F28335

+關注

TMS320F28335是一款TI高性能TMS320C28x系列32位浮點DSP處理器
靜電防護

靜電防護

+關注

為防止靜電積累所引起的人身電擊、火災和爆炸、電子器件失效和損壞，以及對生產(chǎn)的不良影響而采取的防范措施。其防范原則主要是抑制靜電的產(chǎn)生，加速靜電泄漏，進行靜電中和等。
ESP8266

ESP8266

+關注

wifi模塊ESP8266的默認波特率是115200，但是單片機不能達到那么快的傳輸速率，只能使用4800bps，那么設置的時候，必不可少的要先用轉串口調(diào)試下載器。

換一批

電機控制	DSP	氮化鎵	功率放大器	ChatGPT	自動駕駛	TI	瑞薩電子
BLDC	PLC	碳化硅	二極管	OpenAI	元宇宙	安森美	ADI
無刷電機	FOC	IGBT	逆變器	文心一言	5G	英飛凌	羅姆
直流電機	PID	MOSFET	傳感器	人工智能	物聯(lián)網(wǎng)	NXP	賽靈思
步進電機	SPWM	充電樁	IPM	機器視覺	無人機	三菱電機	ST
伺服電機	SVPWM	光伏發(fā)電	UPS	AR	智能電網(wǎng)	國民技術	Microchip

瑞薩	沁恒股份	全志	國民技術	瑞芯微	兆易創(chuàng)新	芯海科技	Altium
德州儀器	Vishay	Micron	Skyworks	AMS	TAIYOYUDEN	納芯微	HARTING
adi	Cypress	Littelfuse	Avago	FTDI	Cirrus LogIC	Intersil	Qualcomm
st	Murata	Panasonic	Altera	Bourns	矽力杰	Samtec	揚興科技
microchip	TDK	Rohm	Silicon Labs	圣邦微電子	安費諾工業(yè)	ixys	Isocom Compo
安森美	DIODES	Nidec	Intel	EPSON	樂鑫	Realtek	ERNI電子
TE Connectivity	Toshiba	OMRON	Sensirion	Broadcom	Semtech	旺宏	英飛凌
Nexperia	Lattice	KEMET	順絡電子	霍尼韋爾	pulse	ISSI	NXP
Xilinx	廣瀨電機	金升陽	君耀電子	聚洵	Liteon	新潔能	Maxim
MPS	億光	Exar	菲尼克斯	CUI	WIZnet	Molex	Yageo
Samsung	風華高科	WINBOND	長晶科技	晶導微電子	上海貝嶺	KOA	Echelon
Coilcraft	LRC	trinamic

放大器	運算放大器	差動放大器	電流感應放大器	比較器	儀表放大器	可變增益放大器	隔離放大器
時鐘	時鐘振蕩器	時鐘發(fā)生器	時鐘緩沖器	定時器	寄存器	實時時鐘	PWM 調(diào)制器
視頻放大器	功率放大器	頻率轉換器	揚聲器放大器	音頻轉換器	音頻開關	音頻接口	音頻編解碼器
模數(shù)轉換器	數(shù)模轉換器	數(shù)字電位器	觸摸屏控制器	AFE	ADC	DAC	電源管理
線性穩(wěn)壓器	LDO	開關穩(wěn)壓器	DC/DC	降壓轉換器	電源模塊	MOSFET	IGBT
振蕩器	諧振器	濾波器	電容器	電感器	電阻器	二極管	晶體管
變送器	傳感器	解析器	編碼器	陀螺儀	加速計	溫度傳感器	壓力傳感器
電機驅動器	步進驅動器	TWS	BLDC	無刷直流驅動器	濕度傳感器	光學傳感器	圖像傳感器
數(shù)字隔離器	ESD 保護	收發(fā)器	橋接器	多路復用器	氮化鎵	PFC	數(shù)字電源

開關電源	步進電機	無線充電	LabVIEW	EMC	PLC	OLED	單片機
5G	m2m	DSP	MCU	ASIC	CPU	ROM	DRAM
NB-IoT	LoRa	Zigbee	NFC	藍牙	RFID	Wi-Fi	SIGFOX
Type-C	USB	以太網(wǎng)	仿真器	RISC	RAM	寄存器	GPU
語音識別	萬用表	CPLD	耦合	電路仿真	電容濾波	保護電路	看門狗
CAN	CSI	DSI	DVI	Ethernet	HDMI	I2C	RS-485
SDI	nas	DMA	HomeKit	閾值電壓	UART	機器學習	TensorFlow

Arduino	BeagleBone	樹莓派	STM32	MSP430	EFM32	ARM mbed	EDA
示波器	LPC	imx8	PSoC	Altium Designer	Allegro	Mentor	Pads
OrCAD	Cadence	AutoCAD	華秋DFM	Keil	MATLAB	MPLAB	Quartus

在线观看www成人影院-在线观看www日本免费网站-在线观看www视频-在线观看操-欧美18在线-欧美1级

搜索歷史

拉普拉斯變換

拉普拉斯變換技術

相關標簽

相關話題

關注此標簽的用戶(1人)

C++	Java	Python	JavaScript	node.js	RISC-V	verilog	Tensorflow
Android	iOS	linux	RTOS	FreeRTOS	LiteOS	RT-THread	uCOS
DuerOS	Brillo	Windows11	HarmonyOS

林超文PCB設計：PADS教程，PADS視頻教程	鄭振宇老師：Altium Designer教程，Altium Designer視頻教程
張飛實戰(zhàn)電子視頻教程	朱有鵬老師：海思HI3518e教程，HI3518e視頻教程
李增老師：信號完整性教程，高速電路仿真教程	華為鴻蒙系統(tǒng)教程，HarmonyOS視頻教程
賽盛：EMC設計教程，EMC視頻教程	杜洋老師：STM32教程，STM32視頻教程
唐佐林：c語言基礎教程，c語言基礎視頻教程	張飛：BUCK電源教程，BUCK電源視頻教程
正點原子：FPGA教程，F(xiàn)PGA視頻教程	韋東山老師：嵌入式教程，嵌入式視頻教程
張先鳳老師：C語言基礎視頻教程	許孝剛老師：Modbus通訊視頻教程
王振濤老師：NB-IoT開發(fā)視頻教程	Mill老師：FPGA教程，Zynq視頻教程
C語言視頻教程	RK3566芯片資料合集
朱有鵬老師：U-Boot源碼分析視頻教程	開源硬件專題