什么是拉普拉斯變換
拉普拉斯變換是工程數(shù)學中常用的一種積分變換,又名拉氏變換。拉氏變換是一個線性變換,可將一個有參數(shù)實數(shù)t(t≥ 0)的函數(shù)轉(zhuǎn)換為一個參數(shù)為復數(shù)s的函數(shù)。拉普拉斯變換在許多工程技術和科學研究領域中有著廣泛的應用,特別是在力學系統(tǒng)、電學系統(tǒng)、自動控制系統(tǒng)、可靠性系統(tǒng)以及隨機服務系統(tǒng)等系統(tǒng)科學中都起著重要作用。
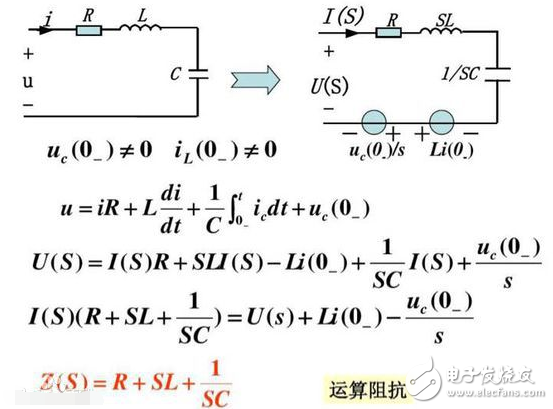
公式概念
拉普拉斯變換[2] 是對于t》=0函數(shù)值不為零的連續(xù)時間函數(shù)x(t)通過關系式
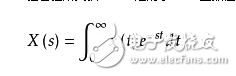
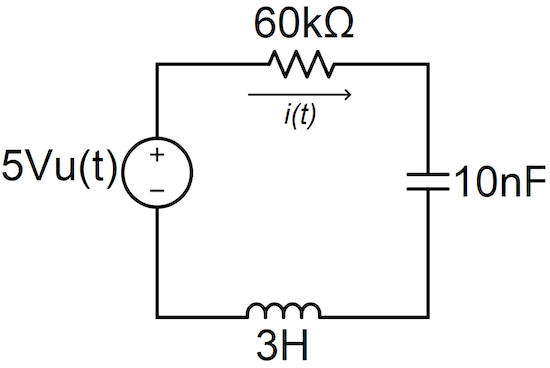
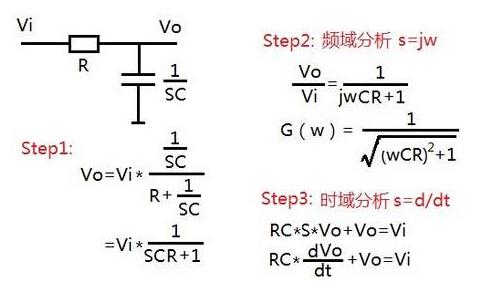
(式中st為自然對數(shù)底e的指數(shù))變換為復變量s的函數(shù)X(s)。它也是時間函數(shù)x(t)的“復頻域”表示方式。據(jù)此,在“電路分析”中,元件的伏安關系可以在復頻域中進行表示,即電阻元件:V=RI,電感元件:V=sLI,電容元件:I=sCV。如果用電阻R與電容C串聯(lián),并在電容兩端引出電壓作為輸出,那么就可用“分壓公式”得出該系統(tǒng)的傳遞函數(shù)為H(s)=(1/RC)/(s+(1/RC)),于是響應的拉普拉斯變換Y(s)就等于激勵的拉普拉斯變換X(s)與傳遞函數(shù)H(s)的乘積,即Y(s)=X(s)H(s)
如果定義:f(t)是一個關于t的函數(shù),使得當t《0時候,f(t)=0;s是一個復變量;mathcal 是一個運算符號,它代表對其對象進行拉普拉斯積分int_0^infty e‘ dt;F(s)是f(t)的拉普拉斯變換結(jié)果。
則f(t),的拉普拉斯變換由下列式子給出:F(s),=mathcal left =int_ ^infty f(t)’ e‘ dt 拉普拉斯逆變換,是已知F(s)’ 求解f(t)的過程。用符號 mathcal‘ 表示。
拉普拉斯逆變換的公式是:對于所有的t》0,f(t)= mathcal ^ left=frac int_ ^ F(s)’ e‘ds,c’ 是收斂區(qū)間的橫坐標值,是一個實常數(shù)且大于所有F(s)‘ 的個別點的實部值。
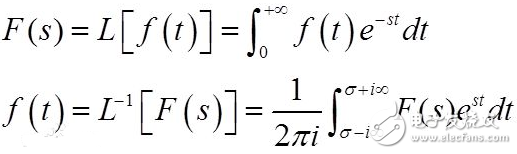
為簡化計算而建立的實變量函數(shù)和復變量函數(shù)間的一種函數(shù)變換。對一個實變量函數(shù)作拉普拉斯變換,并在復數(shù)域中作各種運算,再將運算結(jié)果作拉普拉斯反變換來求得實數(shù)域中的相應結(jié)果,往往比直接在實數(shù)域中求出同樣的結(jié)果在計算上容易得多。拉普拉斯變換的這種運算步驟對于求解線性微分方程尤為有效,它可把微分方程化為容易求解的代數(shù)方程來處理,從而使計算簡化。在經(jīng)典控制理論中,對控制系統(tǒng)的分析和綜合,都是建立在拉普拉斯變換的基礎上的。引入拉普拉斯變換的一個主要優(yōu)點,是可采用傳遞函數(shù)代替微分方程來描述系統(tǒng)的特性。這就為采用直觀和簡便的圖解方法來確定控制系統(tǒng)的整個特性(見信號流程圖、動態(tài)結(jié)構(gòu)圖)、分析控制系統(tǒng)的運動過程(見奈奎斯特穩(wěn)定判據(jù)、根軌跡法),以及綜合控制系統(tǒng)的校正裝置(見控制系統(tǒng)校正方法)提供了可能性。用 f(t)表示實變量t的一個函數(shù),F(xiàn)(s)表示它的拉普拉斯變換,它是復變量s=σ+j&owega;的一個函數(shù),其中σ和&owega; 均為實變數(shù),j2=-1。F(s)和f(t)間的關系由下面定義的積分所確定:
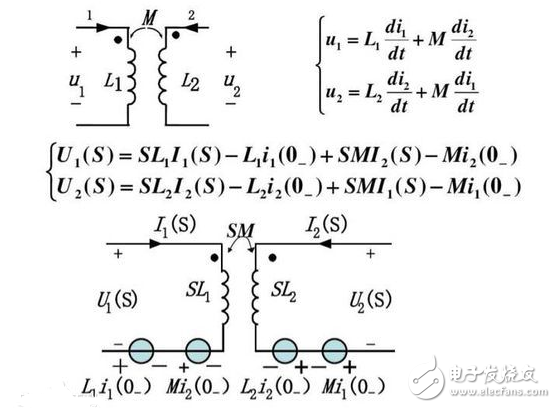
如果對于實部σ 》σc的所有s值上述積分均存在,而對σ ≤σc時積分不存在,便稱 σc為f(t)的收斂系數(shù)。對給定的實變量函數(shù) f(t),只有當σc為有限值時,其拉普拉斯變換F(s)才存在。習慣上,常稱F(s)為f(t)的象函數(shù),記為F(s)=L[f(t)];稱f(t)為F(s)的原函數(shù),記為f(t)=L-1[F(s)]。
函數(shù)變換對和運算變換性質(zhì) 利用定義積分,很容易建立起原函數(shù) f(t)和象函數(shù) F(s)間的變換對,以及f(t)在實數(shù)域內(nèi)的運算與F(s)在復數(shù)域內(nèi)的運算間的對應關系。表1和表2分別列出了最常用的一些函數(shù)變換對和運算變換性質(zhì)。
拉普拉斯變化的存在性:為使F(s)存在,積分式必須收斂。有如下定理:
如因果函數(shù)f(t)滿足:(1)在有限區(qū)間可積,(2)存在σ0使|f(t)|e-σt在t→∞時的極限為0,則對于所有σ大于σ0,拉普拉斯積分式絕對且一致收斂。
基本性質(zhì):線性性質(zhì)、微分性質(zhì)、積分性質(zhì)、位移性質(zhì)、延遲性質(zhì)、初值定理與終值。
應用領域定理
有些情形下一個實變量函數(shù)在實數(shù)域中進行一些運算并不容易,但若將實變量函數(shù)作拉普拉斯變換,并在復數(shù)域中作各種運算,再將運算結(jié)果作拉普拉斯反變換來求得實數(shù)域中的相應結(jié)果,
在經(jīng)典控制理論中,對控制系統(tǒng)的分析和綜合,都是建立在拉普拉斯變換的基礎上的。引入拉普拉斯變換的一個主要優(yōu)點,是可采用傳遞函數(shù)代替常系數(shù)微分方程來描述系統(tǒng)的特性。這就為采用直觀和簡便的圖解方法來確定控制系統(tǒng)的整個特性、分析控制系統(tǒng)的運動過程,以及提供控制系統(tǒng)調(diào)整的可能性。
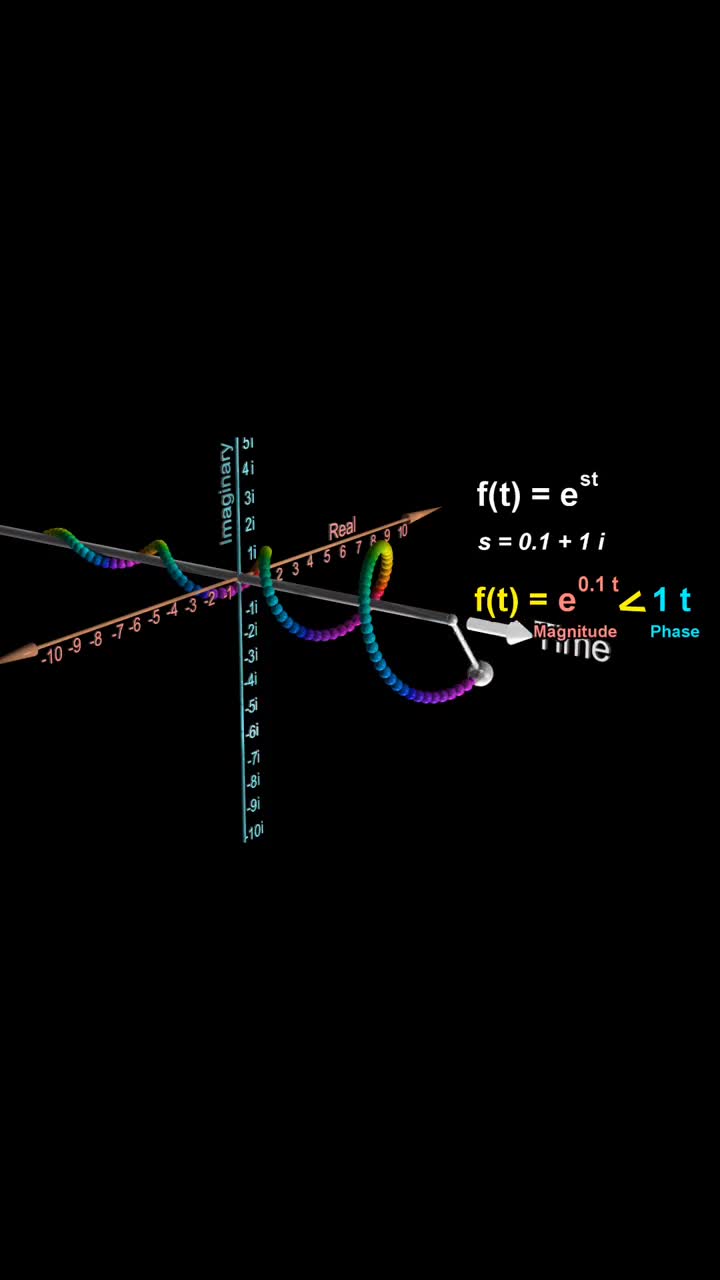
應用拉普拉斯變換解常變量齊次微分方程,可以將微分方程化為代數(shù)方程,使問題得以解決。在工程學上,拉普拉斯變換的重大意義在于:將一個信號從時域上,轉(zhuǎn)換為復頻域(s域)上來表示;在線性系統(tǒng),控制自動化上都有廣泛的應用。
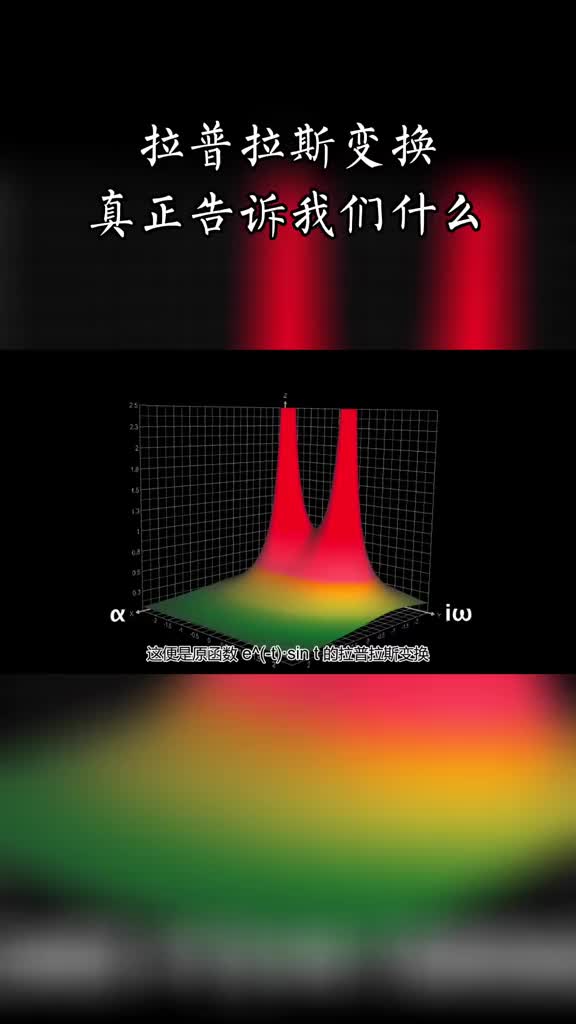
拉普拉斯變換的物理意義是什么?
從正則系綜配分函數(shù)切換到微正則系綜態(tài)密度或者說譜密度的時候,所用的是拉普拉斯逆變換;反之是拉普拉斯變換。其中核的指數(shù)上的復數(shù)也很好理解,它經(jīng)常出現(xiàn)于統(tǒng)計力學中的Lee-Yang理論(由李政道和楊振寧于1952年通過兩篇論文建立):即復化之后的溫度,化學勢或者外磁場。
他們通過這種復化的方法推導出出了在熱力學極限下,系統(tǒng)發(fā)生一級或者連續(xù)相變的條件(原文是對于自旋系統(tǒng)的):就像復分析里的branch cut一樣,Lee-Yang零點在復平面上聚集成一條線,只有取實數(shù)值的物理量在相變是跨過這條線,才會發(fā)生一級相變。這些零點解釋了為什么一個明明是解析函數(shù)的配分函數(shù)在相變時卻能導致發(fā)散的物理量,也給出了一個no-go theorem: 不取熱力學極限就不會發(fā)生相變;至今這套理論還是研究傳統(tǒng)非拓撲相變的利器。有人會說復的物理學量只是數(shù)學技巧罷了,但近來有實驗表明我們是能觀測到Lee-Yang零點的, 跑偏一點,這套理論還衍生出Lee-Yang edge,即高于相變溫度時,上述的Lee-Yang零點匯聚線終止于兩個臨界點,而用于描述該臨界點附近復物理量的理論是一個central charge為-22/5的2維共形場論,叫非幺正minimal model.
因此拉普拉斯變換在研究3維純量子引力(不含費米物質(zhì))特別是黑洞熵以及黑洞Hawking-Page相變的時候,經(jīng)常出現(xiàn)在半經(jīng)典近似中,因為如果假設AdS/CFT成立,復化的熱力學量既屬于2維漸進邊界上的引力邊界條件,也是邊界2維共形場論的參數(shù)。可以參照下列Witten和尹希的文章(Maloney-Witten里(5.7)式附近把拉普拉斯逆變換寫成拉普拉斯變換了)。
PS: Lee-Yang的原文里只考慮了復化的外磁場和化學勢,叫做field-driven transition;復溫度是1965年Michael E. Fisher引入的,叫temperature-driven transition,是一個nontrivial的推廣,注意不要和有限溫度場論中的虛時間混淆。
數(shù)學上,其實把拉普拉斯變換看成Borel變換的推廣比看成是傅里葉變換的推廣更合適,因為后者的指數(shù)上也沒有虛數(shù)單位,專治非收斂級數(shù),這和拉普拉斯變換代替傅里葉變換處理非收斂信號有異曲同工之妙。在物理中的用途嘛,最近在非微擾量子場論和弦論的resurgent analysis里火得不行呀
 電子發(fā)燒友App
電子發(fā)燒友App















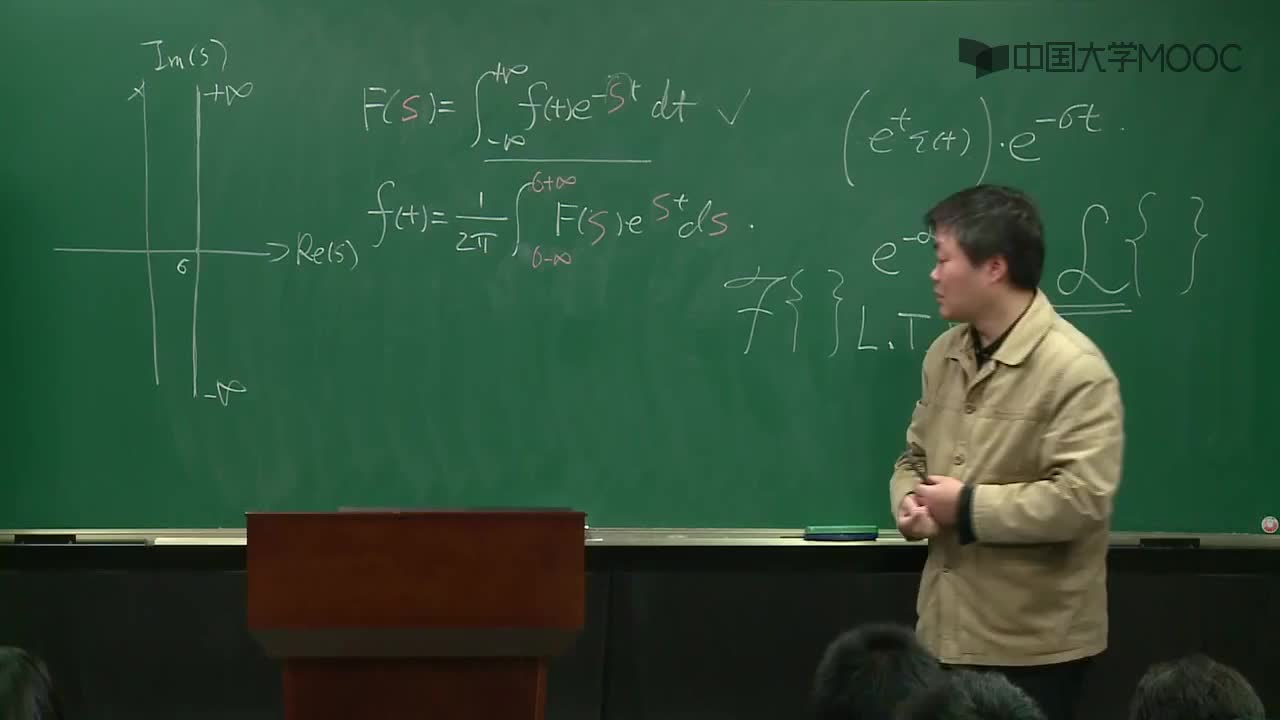






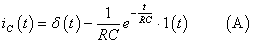
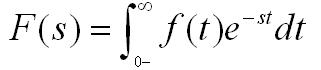
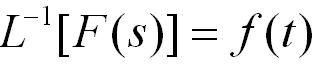










評論