引言
隨著人們生活水平的提高,對汽車舒適性的要求也越來越高。汽車空調(diào)的質(zhì)量影響到對整車的評價(jià)。由于汽車是直接暴露在太陽或風(fēng)雪下,而且汽車行駛的速度變化無常,車內(nèi)的空間有限。這都加大了汽車空調(diào)的設(shè)計(jì)難度。一般來說汽車空調(diào)由壓縮機(jī),冷凝器,蒸發(fā)器,和膨脹閥組成。汽車空調(diào)壓縮機(jī)是汽車空調(diào)的關(guān)鍵零部件,也是主要的運(yùn)動部件。采用虛擬樣機(jī)技術(shù)可以研究汽車空調(diào)壓縮機(jī)的運(yùn)動規(guī)律和動力性能,為設(shè)計(jì)和優(yōu)化提供幫助。
虛擬樣機(jī)技術(shù)是在產(chǎn)品的設(shè)計(jì)開發(fā)中,將分散的零部件設(shè)計(jì)和分析技術(shù)融合在一起,在計(jì)算機(jī)上建造出產(chǎn)品的整體模型,并對該產(chǎn)品在投入使用后的各種工況進(jìn)行仿真分析,預(yù)測產(chǎn)品的整體性能,進(jìn)而改進(jìn)設(shè)計(jì),提高產(chǎn)品質(zhì)量。
本文是采用MSC.ADAMS 軟件對一款汽車空調(diào)壓縮機(jī)進(jìn)行運(yùn)動,動力分析,從而了解其運(yùn)動規(guī)律,并計(jì)算一些聯(lián)接副的受力情況。
1 汽車空調(diào)壓縮機(jī)運(yùn)動機(jī)構(gòu)概述
汽車空調(diào)壓縮機(jī)可分為往復(fù)式和旋轉(zhuǎn)式二大類。往復(fù)式的又分曲軸連桿式,軸向活塞式,和徑向活塞式。其中軸向活塞式又分旋轉(zhuǎn)斜盤式和搖擺斜盤式。旋轉(zhuǎn)式又分刮片式,滾動活塞式,三角轉(zhuǎn)子式,渦旋式,螺桿式。本文主要研究5 缸搖擺斜盤式的汽車空調(diào)壓縮機(jī)。
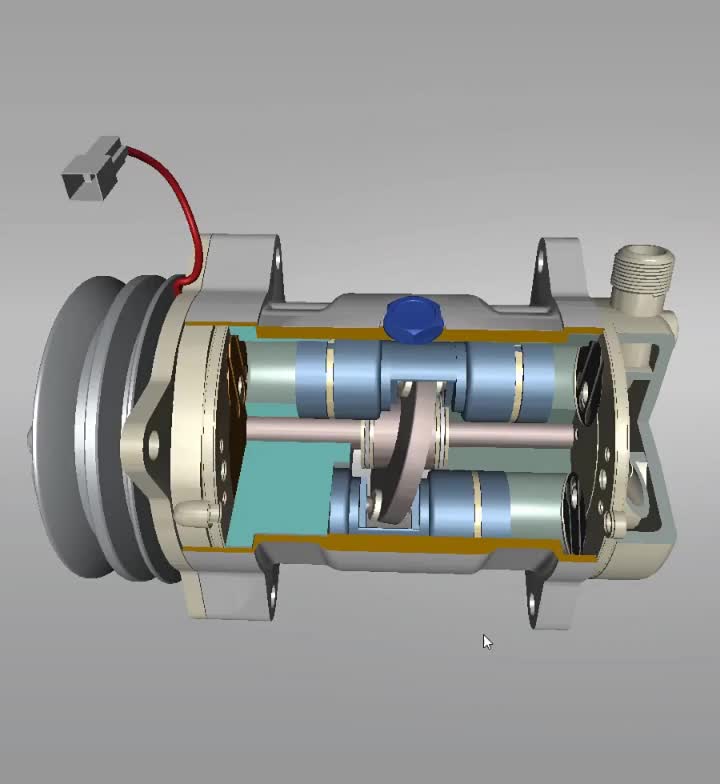
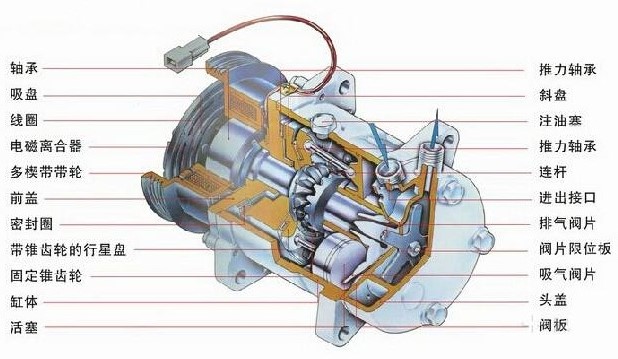
搖擺斜盤式的汽車空調(diào)壓縮機(jī)的工作原理是通過主軸的旋轉(zhuǎn)帶動斜盤的轉(zhuǎn)動,通過只能進(jìn)行擺動的行星盤將旋轉(zhuǎn)運(yùn)動轉(zhuǎn)化為活塞的往復(fù)運(yùn)動,活塞在氣缸里對制冷劑進(jìn)行壓縮。(見圖1)
?
圖1 空調(diào)壓縮機(jī)核心部件裝配圖
2 搖擺斜盤式壓縮機(jī)運(yùn)動學(xué)幾何關(guān)系
搖擺斜盤式壓縮機(jī)通過主軸帶動斜盤作圓周運(yùn)動,行星盤由于導(dǎo)向桿的運(yùn)動約束,將主軸的周轉(zhuǎn)運(yùn)動轉(zhuǎn)化為斜盤表面質(zhì)點(diǎn)的軸向往復(fù),并通過連桿帶動活塞,構(gòu)成空間上類曲柄滑塊機(jī)構(gòu)。
本模型中,由于受到行星盤上導(dǎo)向桿的約束,活塞3 的連桿連接行星盤一端的球心始終位于軸線與導(dǎo)向桿軸線所確定的平面內(nèi),該活塞的運(yùn)動處于較為特殊的地位,幾何關(guān)系為平面運(yùn)動。其余活塞1,5,活塞2,4 互為對等關(guān)系,且均屬空間運(yùn)動學(xué)范疇。
3 活塞運(yùn)動學(xué)公式推導(dǎo)
在研究壓縮機(jī)時(shí),活塞的運(yùn)動規(guī)律十分重要。下面以活塞3 為例,對壓縮機(jī)的活塞質(zhì)心運(yùn)動進(jìn)行公式推導(dǎo)。
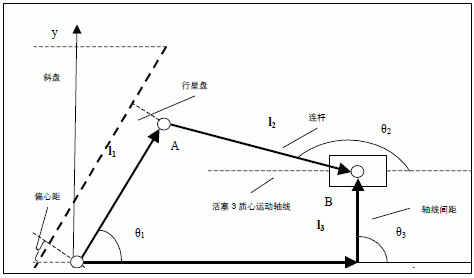
如圖2 所示,對該幾何關(guān)系構(gòu)建封閉矢量多邊形,l1、l2、l3、s4 均為相應(yīng)的桿矢量,θ1、θ2、θ3、θ4 為桿件的方位角,各桿件矢量方向不影響計(jì)算結(jié)果,但方位角均應(yīng)由x 軸開始,并以沿逆時(shí)針方向計(jì)量為正。
?
圖2 活塞3 運(yùn)動幾何關(guān)系
由于主軸軸線(即斜盤軸線)和行星盤軸線各自在工作結(jié)合面(粗虛線)上的交點(diǎn)有一偏心距,其偏置的結(jié)果正好使得行星盤中心球狀腔的球心(O 點(diǎn))落在了主軸軸線(X 軸)上。
所以,在固定球輪的頂壓下,行星盤完全繞O 點(diǎn)作擺動,行星盤中心孔腔的球心(O 點(diǎn))到圓周孔腔(即連桿球鉸鏈落位處)的球心(A 點(diǎn))之間的距離為曲柄長度,連桿兩球心之間距離為連桿長度,活塞質(zhì)心運(yùn)動狀態(tài)等效B 點(diǎn)(球鉸鏈球心)運(yùn)動狀態(tài)。
由于在封閉矢量多邊形中,各矢量之和為零:
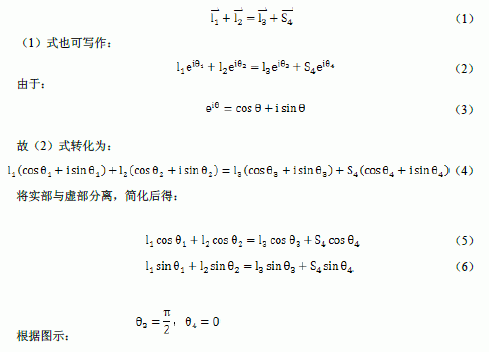
?
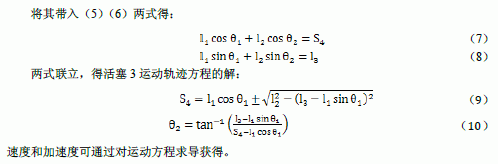
?
4 通過MSC.ADAMS 對壓縮機(jī)進(jìn)行運(yùn)動動力分析
4.1 分析的基本步驟
汽車空調(diào)壓縮機(jī)的仿真過程如下:1. 運(yùn)用UG 的三維實(shí)體建模模塊對壓縮機(jī)核心運(yùn)動機(jī)構(gòu)進(jìn)行三維建模,主要包括主軸、斜盤、行星盤、連桿和活塞五大部件,并在UG 環(huán)境下進(jìn)行裝配。2. 將建好的實(shí)體模型以Parasolid 格式輸出,導(dǎo)入ADAMS 中,添加材料屬性,并根據(jù)默認(rèn)位置關(guān)系附加運(yùn)動約束,實(shí)現(xiàn)模擬運(yùn)動無干涉。3. 根據(jù)三種給定的不同工況,計(jì)算活塞端面的氣體壓力,將氣體力學(xué)方程導(dǎo)入,完成力學(xué)約束的添加。4. 根據(jù)工況,在驅(qū)動軸上賦給指定轉(zhuǎn)速,輸出動力學(xué)特性曲線,包括活塞質(zhì)心位移曲線、活塞質(zhì)心速度曲線、活塞質(zhì)心加速度曲線和活塞端面力曲線。并對獲取的數(shù)據(jù)進(jìn)行動力學(xué)分析。
4.2 零部件的物理參數(shù)
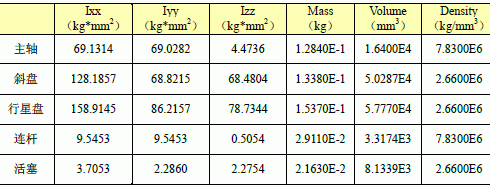
其幾何參數(shù)和慣性參數(shù)采用三維CAD 實(shí)體建模軟件UG-Ⅱ計(jì)算得到,如表1 所示。這對幾何形狀極不規(guī)則,采用計(jì)算方法很難得到準(zhǔn)確數(shù)值的物體,如斜盤等,將大大簡化計(jì)算過程。
表1 空調(diào)壓縮核心部件力學(xué)參數(shù)
?
4.3 約束的選定
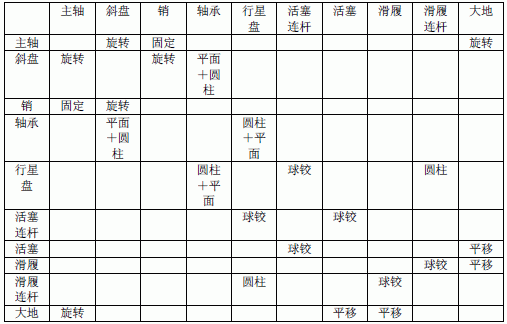
在ADAMS 的VIEW 模塊對模型中的零件之間的運(yùn)動副進(jìn)行約束定義。下表為運(yùn)動副的約束定義。
表2 空調(diào)壓縮核心部件運(yùn)動約束
?
4.4 確定邊界條件(活塞壓力的確定)
4.4.1 仿真工況:
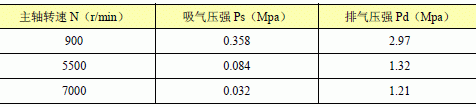
按試驗(yàn)要求,如表4.2.3-1 所示,仿真過程將在900rps、5500rps、7000rps 三種轉(zhuǎn)速及各自相對應(yīng)的吸氣壓強(qiáng)、排氣壓強(qiáng)下進(jìn)行測試。
表3 空調(diào)壓縮機(jī)試驗(yàn)工況
?
4.4.2 活塞頂部壓力公式推導(dǎo):
根據(jù)氣體方程:多變過程的 P*VN=C 得出:
壓縮過程:P1=Ps*((L+C)/( .5H11G.cm_dis+d3+C)) N
排氣過程:P2=Pd
膨脹過程:P3=Pd*(C/(.5H11G.cm_dis+d3+C)) N
吸氣過程:P4=Ps
其中:
L=壓縮機(jī)平均行程
C=余隙
N=多變指數(shù)
d3=活塞下止點(diǎn)平均位置
.5H11G.cm_dis=活塞質(zhì)心點(diǎn)位置
4.4.3 多變指數(shù)的確定
實(shí)際熱機(jī)中,有些過程工質(zhì)的狀態(tài)參數(shù)p、v、T 等都有顯著的變化,與外界之間換熱量也不可忽略不計(jì),這時(shí)它們不能簡化為四種基本的熱力學(xué)過程(定容、定壓、定溫和絕熱)。試驗(yàn)測定了一些過程中1kg 工質(zhì)的壓力p 和v 的關(guān)系,發(fā)現(xiàn)它們接近指數(shù)函數(shù),用數(shù)學(xué)表達(dá)式描述即:p*vn=定值。該式即多變過程的過程方程式。n 為多變指數(shù),它可以是負(fù)無窮到正無窮之間的任意數(shù)值。多變過程比前述幾種特殊過程更為一般化,但也并非任意的過程,它仍根據(jù)一定的規(guī)律變化:整個過程服從過程方程p*vN=定值,n 為某一定值。
實(shí)際過程往往更為復(fù)雜。譬如柴油機(jī)氣缸中的壓縮過程,開始時(shí)工質(zhì)溫度低于缸壁溫度,邊吸熱邊壓縮而溫度升高,高于缸壁溫度后則邊壓縮邊放熱,整個過程n 大約從1.6 變化到1.2 左右;至于膨脹過程,由于存在后燃及高溫時(shí)被離解氣體的復(fù)合放熱現(xiàn)象,情況更為復(fù)雜,其散熱規(guī)律的研究已不屬于熱力學(xué)的范圍。對于多變指數(shù)n 式變化的實(shí)際過程,若n 的變化范圍不大,則可用一個不變的平均值近似地代替實(shí)際變化地n;若n 地變化較大,則可將實(shí)際過程分成數(shù)段,每一段都近似為n 值不變。
本課題中,由于n 值的變化范圍不大,根據(jù)以往實(shí)際工況和以往經(jīng)驗(yàn),選取n=1.3。
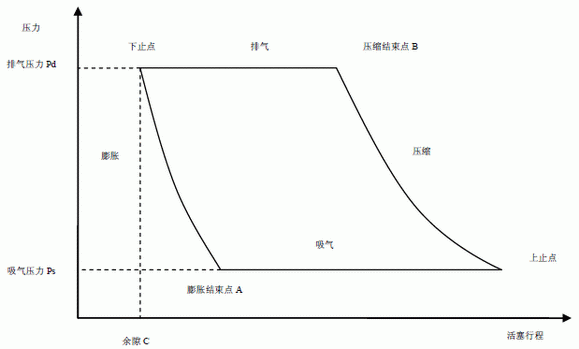
如圖3 所示,壓縮和膨脹為多變過程,多變指數(shù)n=1.3。膨脹結(jié)束點(diǎn)A 的壓力應(yīng)小于吸氣壓力Ps,壓縮結(jié)束點(diǎn)B 的壓力應(yīng)大于排氣壓力Pd,但考慮影響有限,故膨脹結(jié)束點(diǎn)A 的壓力=Ps,壓縮結(jié)束點(diǎn)B 的壓力=Pd。
?
圖 3 壓縮機(jī)整個行程中的P-V 關(guān)系
4.4.4 活塞頂部壓力在運(yùn)動分析中的體現(xiàn):
4.4.4.1 MSC.ADAMS 中IF 函數(shù)的定義
IF(expr1:expr2,expr3,expr4)
式中,expr1 為控制變量,expr2,expr3 和expr4 均為表達(dá)式。
函數(shù)F=IF(expr1:expr2,expr3,expr4)的含義為:
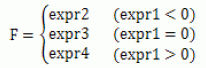
?
4.4.4.2 在本課題中IF 語句算法
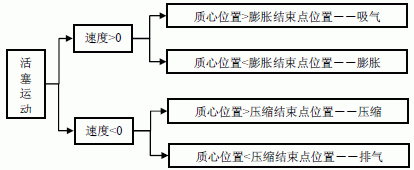
圖4 所示為本課題中壓縮機(jī)活塞端面受力IF 語句算法。先由活塞的速度方向(大于零/小于零),判斷活塞運(yùn)動處于吸氣/膨脹狀態(tài),還是壓縮/排氣狀態(tài),再根據(jù)活塞質(zhì)心位置與膨脹結(jié)束點(diǎn)的關(guān)系確定是吸氣狀態(tài)還是膨脹狀態(tài);根據(jù)活塞質(zhì)心位置與壓縮結(jié)束點(diǎn)關(guān)系確定是壓縮狀態(tài)還是排氣狀態(tài)。
?
圖4 活塞端面受力IF 語句算法
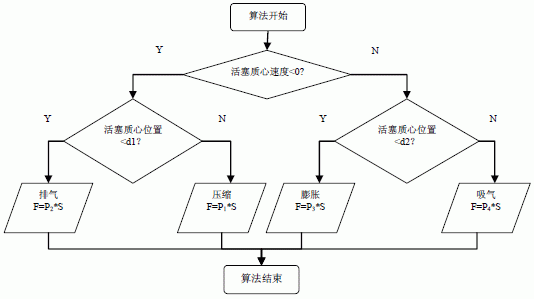
程序框圖如圖5 所示:
?
圖5 活塞端面受力IF 語句程序框圖
4.4.4.3 If 語句公式
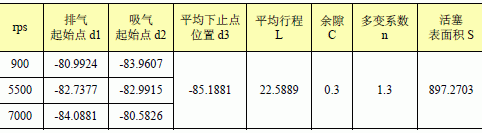
將在UG 中建好的模型導(dǎo)入ADAMS 后,根據(jù)實(shí)際情況施加所需的運(yùn)動約束。設(shè)定End Time = 10,step = 100,進(jìn)行初步動態(tài)運(yùn)行,測量所得數(shù)據(jù)。根據(jù)上述數(shù)據(jù)經(jīng)過計(jì)算,得出在三種不同工況下,活塞的排氣點(diǎn)d1,吸氣點(diǎn)d2 的位置,如表5 所示。
表5 壓縮機(jī)活塞行程參數(shù)(2)
?
以活塞3 在工況900rps 下端面受力為例:吸氣壓力Ps=0.358MPa, 排氣壓力Pd=2.97MPa, 排氣起始點(diǎn)位置d1=-80.9924, 吸氣起始點(diǎn)位置d2=-83.9607,活塞平均下止點(diǎn)位置d3=-85.1881, 活塞表面積S=897.2703, 活塞平均行程L=22.5889,余隙C=0.3,多變系數(shù)n=1.3。
900r/min:
Piston_3 氣體方程:
IF( VZ(piston3.cm):
IF(.5H11G.cm_dis3+80.9924:897.2703*2.97,897.2703*2.97,897.2703*0.358*((22.5889+0.3)/( .5H11G.cm_dis3+85.1881+0.3))**1.3),
IF(.5H11G.cm_dis3+80.9924:897.2703* 0.358, 897.2703*2.97, 897.2703 *2.97),
IF(.5H11G.cm_dis3+83.9607:897.2703*2.97*(0.3/(.5H11G.cm_dis3+85.1881+0.3))**1.3, 897.2703*0.358, 897.2703*0.358)
)
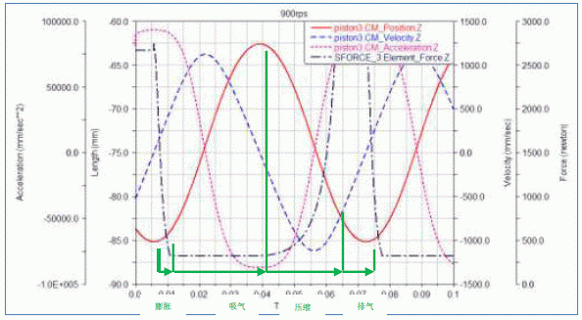
在模型上施加運(yùn)動學(xué)約束以及力約束后,進(jìn)行900rps 的運(yùn)動仿真,以活塞3 為例,摘取其位移、速度、加速度與受力的曲線圖,根據(jù)先前算出的d1、d2 位置,判定活塞在整個行程中的四個階段的狀態(tài)。一個周期內(nèi)壓縮機(jī)進(jìn)行膨脹——吸氣——壓縮——排氣為一次完整循環(huán)。狀態(tài)判定結(jié)果如圖6 所示。
?
圖6 位移、速度、加速度與受力的曲線圖
5 分析結(jié)果
5.1 運(yùn)動學(xué)分析
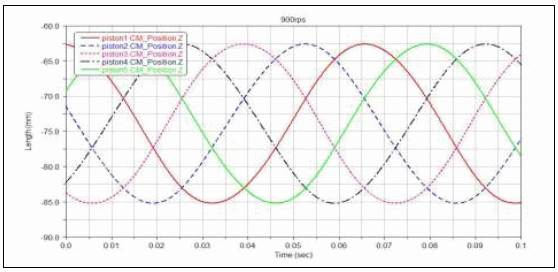
在轉(zhuǎn)速為900rpm、吸氣壓強(qiáng)為0.358Mpa、排氣壓強(qiáng)為2.97Mpa 的工況下,如圖7 和圖8 所示,由于正五邊形的對稱性,所有活塞的位移幅值和端面受力曲線基本一致,相位差為2π /5。
?
圖7 活塞位移曲線(900rpm)
?
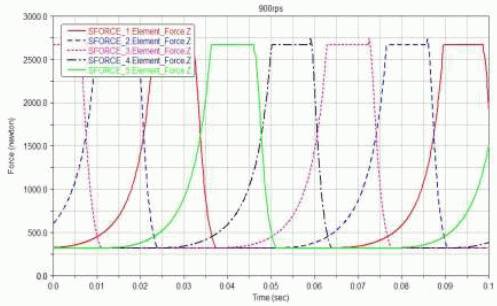
圖8 活塞壓力曲線(900rpm)
在活塞端面受力曲線中可以很明顯的看到兩段壓力恒定的直線,對應(yīng)了壓縮機(jī)工作中的吸氣和排氣狀態(tài)(上端為吸氣,下端為排氣),兩段曲線則分別對應(yīng)了膨脹和壓縮狀態(tài)(左端為壓縮,右端為膨脹),和上文利用速度方向和活塞質(zhì)心位置判定結(jié)果一致。
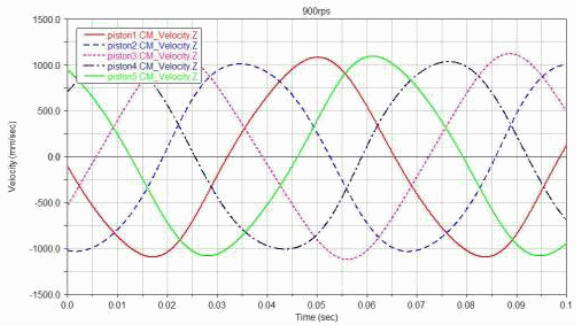
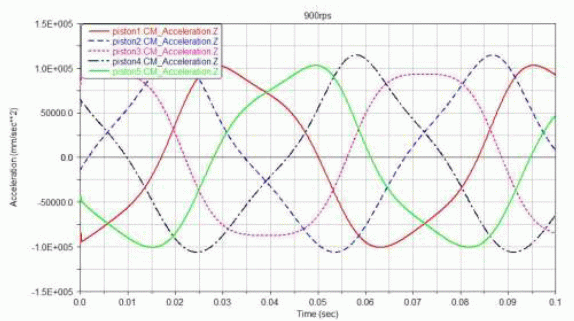
由于導(dǎo)向桿的約束所帶來的對稱性,使得靠近導(dǎo)向桿軸線的活塞(1 和5),其速度幅值要略大于遠(yuǎn)離軸線的活塞(2 和4)速度幅值,如圖9 所示。導(dǎo)向桿所帶來的對稱性在加速度曲線圖中尤為明顯,如圖10 所示,且處于對稱軸線上的活塞3 的加速度曲線變化平穩(wěn)而光滑,遠(yuǎn)離軸線的活塞(1 和5)的加速度曲線則出現(xiàn)了一定的畸變,加速度的峰值相對原相位出現(xiàn)了超前或滯后的現(xiàn)象。
?
圖9 活塞速度曲線(900rpm)
?
圖10 活塞加速度曲線(900rpm)
出現(xiàn)這種情況在很大程度上是由于導(dǎo)向桿的運(yùn)動約束造成的“軸對稱性”而非理想狀態(tài)下的空間對稱性,五個活塞在機(jī)構(gòu)上并不處于完全對等的地位所致。在滿足了五個活塞在周向位移的要求的同時(shí),因?yàn)檫B桿與行星盤的球鉸鏈球心有不同程度的空間運(yùn)動,使得速度和加速度的傳遞出現(xiàn)了不同的結(jié)果。
5.2 動力學(xué)分析
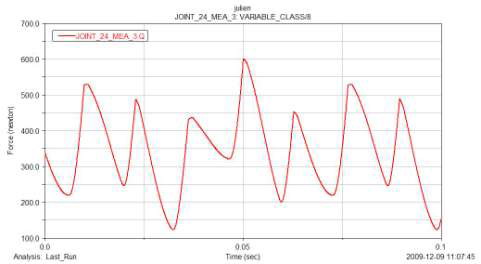
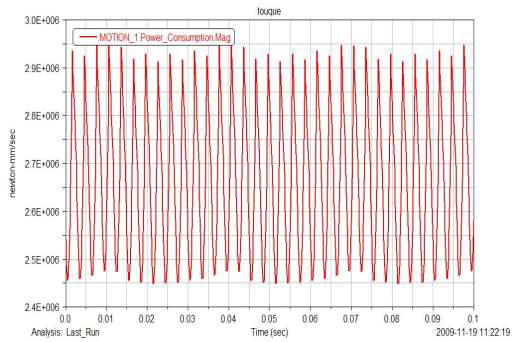
通過分析可得導(dǎo)向桿頭部的受力情況(圖11)和壓縮機(jī)的功耗(圖12)。通過導(dǎo)向桿的受力曲線我們可將其作為有限元分析的邊界條件,分析其應(yīng)力,應(yīng)變,和疲勞。
通過將模擬所得的功耗同實(shí)際情況的功耗進(jìn)行比較,按標(biāo)準(zhǔn)在該工況下功耗應(yīng)為2.75KW,同模擬所得的曲線平均在2.7KW 是相當(dāng)接近的,從而也可證明分析的精度是非常高的。
?
圖11 導(dǎo)向桿頭部受力曲線
?
圖12 壓縮機(jī)功耗曲線
6. 結(jié)語
通過分析,我們發(fā)現(xiàn)理論公式推導(dǎo),和試驗(yàn)數(shù)據(jù)同軟件運(yùn)動學(xué)動力學(xué)仿真所得數(shù)據(jù)能達(dá)成較好的一致性。這說明前期三維實(shí)體建模和實(shí)體模型上的力學(xué)模型搭建的正確性,并進(jìn)一步驗(yàn)證了軟件動力學(xué)仿真的可行性。這不僅節(jié)省了大量的人力物力資源,更重要的是縮短了產(chǎn)品設(shè)計(jì)周期以減短了產(chǎn)品的生產(chǎn)制造周期,提高了優(yōu)化設(shè)計(jì)的便捷性,降低了成本。
 電子發(fā)燒友App
電子發(fā)燒友App


























評論