”張正友標定”是指張正友教授1998年提出的單平面棋盤格的攝像機標定方法。文中提出的方法介于傳統標定法和自標定法之間,但克服了傳統標定法需要的高精度標定物的缺點,而僅需使用一個打印出來的棋盤格就可以。同時也相對于自標定而言,提高了精度,便于操作。因此張氏標定法被廣泛應用于計算機視覺方面。
原理
1.計算外參
設三維世界坐標的點為M=[X,Y,Z,1]T,二維相機平面像素坐標為m=[u,v,1]T,所以標定用的棋盤格平面到圖像平面的單應性關系為:sm=A[R,t]M
其中

不妨設棋盤格位于Z = 0,定義旋轉矩陣R的第i列為 ri, 則有:
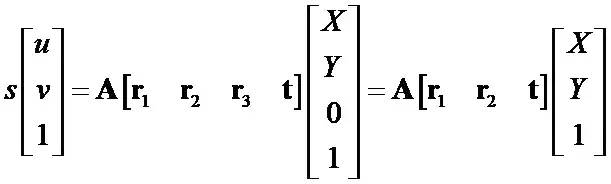
令H=[h1 h2 h3]=λA[r1 r2 t]
于是空間到圖像的映射可改為:sm=HM,
其中H是描述Homographic矩陣,H是一個齊次矩陣,所以有8個未知數,至少需要8個方程,每對對應點能提供兩個方程,所以至少需要四個對應點,就可以算出世界平面到圖像平面的單應性矩陣H

外參具體計算公式。注意:R3是 t
一般而言,求解出的R = [r1 r2 t] 不會滿足正交與歸一的標準
在實際操作中,R 可以通過SVD分解實現規范化(詳見原文)
2.計算內參
由r1和r2正交,且r1和r2的模相等,可以得到如下約束:
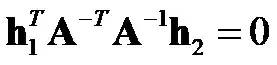
正交
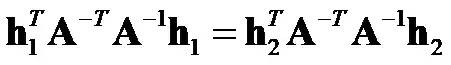
模相等


可以推到出
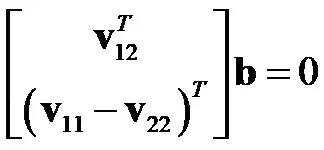
根據推到的結果可知如果有n組觀察圖像,則V 是 2n x 6 的矩陣
根據最小二乘定義,V b = 0 的解是 VTV 最小特征值對應的特征向量。
因此, 可以直接估算出 b,后續可以通過b求解內參
因為B中的未知量為6個,
所以當觀測平面 n ≥ 3 時,可以得到b的唯一解
當 n = 2時, 一般可令畸變參數γ = 0
當 n = 1時, 僅能估算出α 與 β, 此時一般可假定像主點坐標 u0 與 v0 為0
內部參數可通過如下公式計算(cholesky分解):
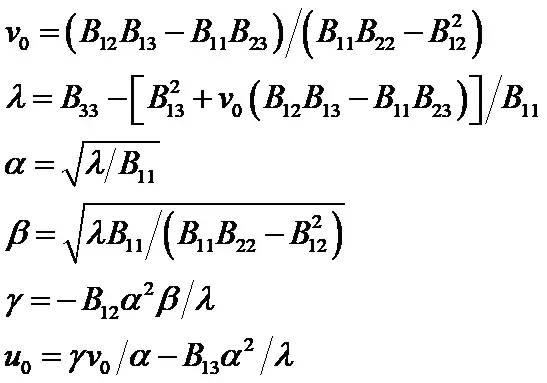
內參具體計算公式
3.最大似然估計
上述的推導結果是基于理想情況下的解,但由于可能存在高斯噪聲,所以使用最大似然估計進行優化。設我們采集了n副包含棋盤格的圖像進行定標,每個圖像里有棋盤格角點m個。令第i副圖像上的角點Mj在上述計算得到的攝像機矩陣下圖像上的投影點為:
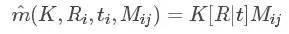
這里的K為相機內參矩陣A
其中Ri和ti是第i副圖對應的旋轉矩陣和平移向量,K是內參數矩陣。則角點mij的概率密度函數為:
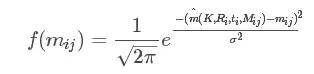
這里的K為相機內參矩陣A
構造似然函數:
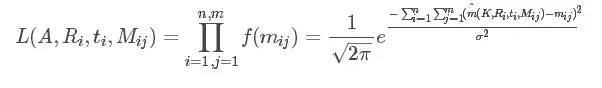
這里的K為相機內參矩陣A
讓L取得最大值,即讓下面式子最小。這里使用的是多參數非線性系統優化問題的Levenberg-Marquardt算法[2]進行迭代求最優解。
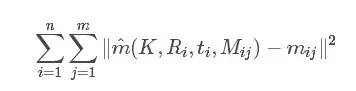
這里的K為相機內參矩陣A
4.徑向畸變估計
張氏標定法只關注了影響最大的徑向畸變。則數學表達式為:
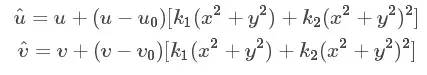
其中,(u,v)是理想無畸變的像素坐標,(u,v)(u,v)是實際畸變后的像素坐標。(u0,v0)代表主點,(x,y)是理想無畸變的連續圖像坐標,(x,y)(x,y)是實際畸變后的連續圖像坐標。k1和k2為前兩階的畸變參數。
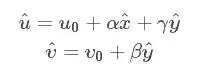
化作矩陣形式:
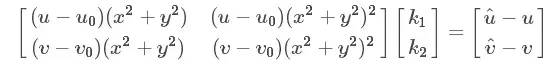
記做:Dk=d
則可得:
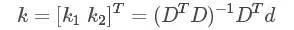
計算得到畸變系數k。
使用最大似然的思想優化得到的結果,即像上一步一樣,LM法計算下列函數值最小的參數值:
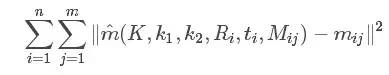
這里的K為相機內參矩陣A
到此,張氏標定法介紹完畢。我們也得到了相機內參、外參和畸變系數。
相機標定步驟
打印一張棋盤格A4紙張(黑白間距已知),并貼在一個平板上
針對棋盤格拍攝若干張圖片(一般10-20張)
在圖片中檢測特征點(Harris特征)
利用解析解估算方法計算出5個內部參數,以及6個外部參數
根據極大似然估計策略,設計優化目標并實現參數的refinement。
審核編輯:劉清
-
攝像機
+關注
關注
3文章
1691瀏覽量
61125 -
計算機視覺
+關注
關注
9文章
1706瀏覽量
46607 -
SVD
+關注
關注
0文章
21瀏覽量
12306
原文標題:張正友標定算法原理詳解
文章出處:【微信號:機器視覺沙龍,微信公眾號:機器視覺沙龍】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
陶瓷標定板技術--宏誠光學

《聊一聊ZXDoc》之汽車標定、臺架標定、三高標定

TIDA-00254使用SDK進行物體點云重建時在系統標定時DLP不打光,怎么解決?
肇觀電子首發自標定3D深度相機
請問做反射式血氧飽和度測量時如何進行標定呢?
友達光電的Micro LED生產線預計2025年啟動量產
傳感器靜態標定的主要步驟是什么
使用基于模型的標定提高開發效率
基于CW32的儀表精度測量實現(三):標定與校準

請問PGA308EVM標定時是否有禁用編程管腳?
康謀技術 | 自動駕駛傳感器標定技術:從單一到聯合標定






 張正友標定算法是什么意思
張正友標定算法是什么意思












評論