本文從最基礎的概率論到各種概率分布全面梳理了基本的概率知識與概念，這些概念可能會幫助我們了解機器學習或開拓視野。這些概念是數據科學的核心，并經常出現在各種各樣的話題上。重溫基礎知識總是有益的，這樣我們就能發現以前并未理解的新知識。

簡介

在本系列文章中，我想探討一些統計學上的入門概念，這些概念可能會幫助我們了解機器學習或開拓視野。這些概念是數據科學的核心，并經常出現在各種各樣的話題上。重溫基礎知識總是有益的，這樣我們就能發現以前并未理解的新知識，所以我們開始吧。

第一部分將會介紹概率論基礎知識。

概率

我們已經擁有十分強大的數學工具了，為什么我們還需要學習概率論？我們用微積分來處理變化無限小的函數，并計算它們的變化。我們使用代數來解方程，我們還有其他幾十個數學領域來幫助我們解決幾乎任何一種可以想到的難題。

難點在于我們都生活在一個混亂的世界中，多數情況下無法準確地測量事物。當我們研究真實世界的過程時，我們想了解許多影響實驗結果的隨機事件。不確定性無處不在，我們必須馴服它以滿足我們的需要。只有如此，概率論和統計學才會發揮作用。

如今，這些學科處于人工智能，粒子物理學，社會科學，生物信息學以及日常生活中的中心。

如果我們要談論統計學，最好先確定什么是概率。其實，這個問題沒有絕對的答案。我們接下來將闡述概率論的各種觀點。

頻率

想象一下，我們有一枚硬幣，想驗證投擲后正反面朝上頻率是否相同。我們如何解決這一問題？我們試著進行一些實驗，如果硬幣正面向上記錄 1，如果反面向上記錄 0。重復投擲 1000 次并記錄 0 和 1 的次數。在我們進行了一些繁瑣的時間實驗后，我們得到了這些結果：600 個正面（1）和 400 反面（0）。如果我們計算過去正面和反面的頻率，我們將分別得到 60％和 40％。這些頻率可以被解釋為硬幣出現正面或者反面的概率。這被稱為頻率化的概率。

條件概率

通常，我們想知道某些事件發生時其它事件也發生的概率。我們將事件 B 發生時事件 A 也發生的條件概率寫為 P（A | B）。以下雨為例：

打雷時下雨的概率有多大？

晴天時下雨的概率有多大？

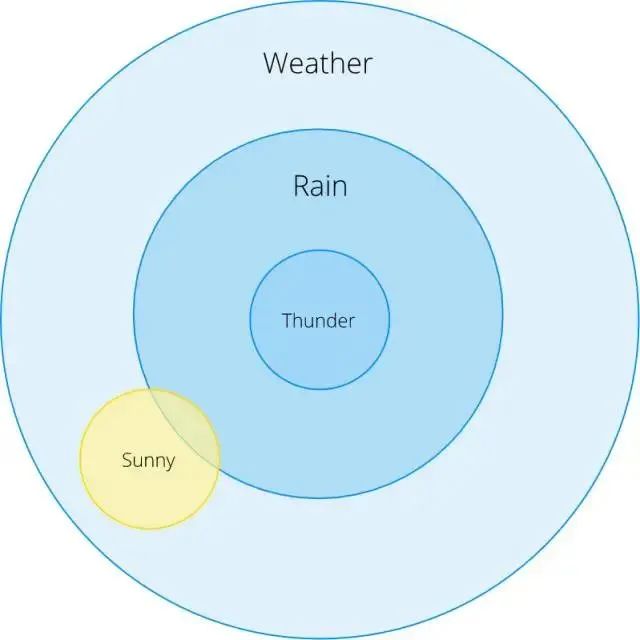
從這個歐拉圖，我們可以看到 P（Rain | Thunder）= 1 ：當我們看到雷聲時，總會下雨（當然，這不完全正確，但是我們在這個例子中保證它成立）。

P（Rain | Sunny）是多少呢？直覺上這個概率很小，但是我們怎樣才能在數學上做出這個準確的計算呢？條件概率定義為：

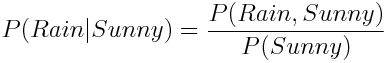
換句話說，我們用 Rain 且 Sunny 的概率除以 Sunny 的概率。

相依事件與獨立事件

如果一個事件的概率不以任何方式影響另一個事件，則該事件被稱為獨立事件。以擲骰子且連續兩次擲得 2 的概率為例。這些事件是獨立的。我們可以這樣表述

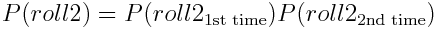
但是為什么這個公式可行？首先，我們將第一次投擲和第二次投擲的事件重命名為 A 和 B，以消除語義影響，然后將我們看到的兩次投擲的的聯合概率明確地重寫為兩次投擲的單獨概率乘積：

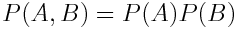
現在用 P（A）乘以 P（B）（沒有變化，可以取消）并重新回顧條件概率的定義：

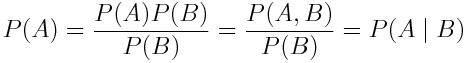
如果我們從右到左閱讀上式，我們會發現 P(A | B) = P(A)。這就意味著事件 A 獨立于事件 B！P（B）也是一樣，獨立事件的解釋就是這樣。

貝葉斯概率論

貝葉斯可以作為一種理解概率的替代方法。頻率統計方法假設存在我們正在尋找的模型參數的一個最佳的具體組合。另一方面，貝葉斯以概率方式處理參數，并將其視為隨機變量。在貝葉斯統計中，每個參數都有自己的概率分布，它告訴我們給已有數據的參數有多種可能。數學上可以寫成

這一切都從一個允許我們基于先驗知識來計算條件概率的簡單的定理開始：

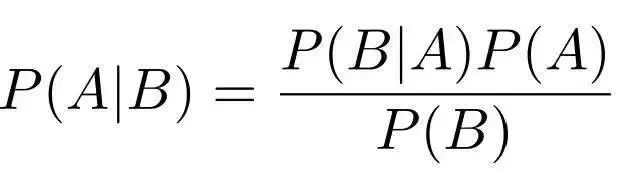
盡管貝葉斯定理很簡單，但它具有巨大的價值，廣泛的應用領域，甚至是貝葉斯統計學的特殊分支。有一個關于貝葉斯定理的非常棒的博客文章，如果你對貝葉斯的推導感興趣---這并不難。

抽樣與統計

假設我們正在研究人類的身高分布，并渴望發表一篇令人興奮的科學論文。我們測量了街上一些陌生人的身高，因此我們的測量數據是獨立的。我們從真實人群中隨機選擇數據子集的過程稱為抽樣。統計是用來總結采樣值數據規律的函數。你可能見過的統計量是樣本均值：

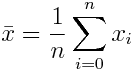
另一個例子是樣本方差：

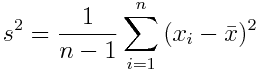
這個公式可以得出所有數據點偏離平均值的程度。

分布

什么是概率分布？這是一個定律，它以數學函數的形式告訴我們在一些實驗中不同可能結果的概率。對于每個函數，分布可能有一些參數來調整其行為。

當我們計算硬幣投擲事件的相對頻率時，我們實際上計算了一個所謂經驗概率分布。事實證明，世界上許多不確定的過程可以用概率分布來表述。例如，我們的硬幣結果是一個伯努利分布，如果我們想計算一個 n 次試驗后硬幣正面向上的概率，我們可以使用二項式分布。

引入一個類似于概率環境中的變量的概念會方便很多--隨機變量。每個隨機變量都具有一定的分布。隨機變量默認用大寫字母表示，我們可以使用 ~ 符號指定一個分布賦給一個變量。

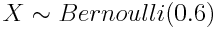
上式表示隨機變量 X 服從成功率（正面向上）為 0.6 的伯努利分布。

連續和離散概率分布

概率分布可分為兩種：離散分布用于處理具有有限值的隨機變量，如投擲硬幣和伯努利分布的情形。離散分布是由所謂的概率質量函數（PMF）定義的，連續分布用于處理連續的（理論上）有無限數量的值的隨機變量。想想用聲音傳感器測量的速度和加速度。連續分布是由概率密度函數（PDF）定義的。

這兩種分布類型在數學處理上有所不同：通常連續分布使用積分 ∫ 而離散分布使用求和Σ。以期望值為例：

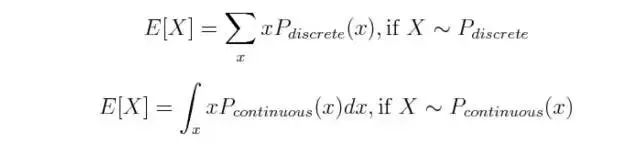
下面我們將詳細介紹各種常見的概率分布類型，正如上所說，概率分布可以分為離散型隨機變量分布和連續性隨機變量分布。離散型隨機變量分布常見的有伯努利分布（Bernoulli Distribution）、二項分布（Binomial Distribution）、泊松分布（Poisson Distribution）等，而常見的連續型隨機變量分布包括均勻分布（Uniform Distribution）、指數分布（Exponential Distribution）、正態分布等。

常見的數據類型

在解釋各種分布之前，我們先看看常見的數據類型有哪些，數據類型可分為離散型和連續型。

離散型數據：數據只能取特定的值，比如，當你擲一個骰子的時候，可能的結果只有 1，2，3，4，5，6 而不會是 1.5 或者 2.45。

連續型數據：數據可以在給定的范圍內取任何值，給定的范圍可以是有限的或無限的，比如一個女孩的體重或者身高，或者道路的長度。一個女孩的體重可以是 54 kgs，54.5 kgs，或 54.5436kgs。

分布的類型

伯努利分布

最簡單的離散型隨機變量分布是伯努利分布，我們從這里開始討論。

一個伯努利分布只有兩個可能的結果，記作 1（成功）和 0（失敗），只有單次伯努利試驗。設定一個具有伯努利分布的隨機變量 X，取值為 1 即成功的概率為 p，取值為 0 即失敗的概率為 q 或者 1-p。

若隨機變量 X 服從伯努利分布，則概率函數為：

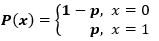
成功和失敗的概率不一定要相等。比如當我和一個運動員打架的時候，他的勝算應該更大，在這時候，我的成功概率是 0.15，而失敗概率是 0.85。

下圖展示了我們的戰斗的伯努利分布。

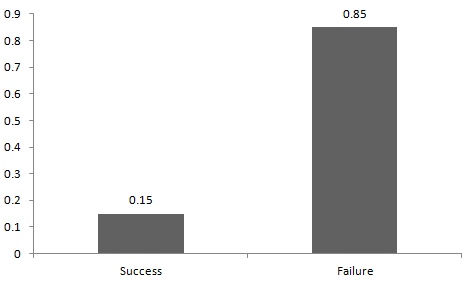
如上圖所示，我的成功概率=0.15，失敗概率=0.85。期望值是指一個概率分布的平均值，對于隨機變量 X，對應的期望值為：E(X) = 1*p + 0*(1-p) = p，而方差為 V(X) = E(X^2) – [E(X)]^2 = p – p^2 = p(1-p)

實際上還有很多關于伯努利分布的例子，比如明天是晴天還是雨天，這場比賽中某一隊輸還是贏，等等。

二項分布

現在回到擲硬幣的案例中，當擲完第一次，我們可以再擲一次，也就是存在多個伯努利試驗。第一次為正不代表以后也會為正。那么設一個隨機變量 X，它表示我們投擲為正面的次數。X 可能會取什么值呢？在投擲硬幣的總次數范圍內可以是任何非負整數。

如果存在一組相同的隨機事件，即一組伯努利試驗，在上例中為連續擲硬幣多次。那么某隨機事件出現的次數即概率服從于二項分布，也稱為多重伯努利分布。

任何一次試驗都是互相獨立的，前一次試驗不會影響當前試驗的結果。兩個結果概率相同的試驗重復 n 次的試驗稱為多次伯努利試驗。二項分布的參數為 n 和 p，n 是試驗的總次數，p 是每一次試驗的成功概率。

根據以上所述，一個二項分布的性質為：

1. 每一次試驗都是獨立的；

2. 只有兩個可能的結果；

3. 進行 n 次相同的試驗；

4. 所有試驗中成功率都是相同的，失敗的概率也是相同的。

二項分布的數學表達式為：

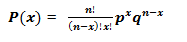
成功概率和失敗概率不相等的二項分布看起來如下圖所示：

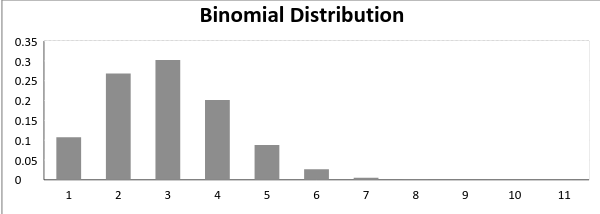
而成功概率和失敗概率相等的二項分布看起來如下圖所示：

二項分布的平均值表示為 μ = n*p，而方差可以表示為 Var(X) = n*p*q。

泊松分布

如果你在一個呼叫中心工作，一天內會接到多少次呼叫呢？多少次都可能！在呼叫中心一天能接到多少次呼叫可以用泊松分布建模。這里有幾個例子：

1. 一天內醫院接到的緊急呼叫次數；

2. 一天內地方接到的偷竊事件報告次數；

3. 一小時內光顧沙龍的人數；

4. 一個特定城市里報告的自殺人數；

5. 書的每一頁的印刷錯誤次數。

現在你可以按相同的方式構造很多其它的例子。泊松分布適用于事件發生的時間和地點隨機分布的情況，其中我們只對事件的發生次數感興趣。泊松分布的主要特點為如下：

1. 任何一個成功事件不能影響其它的成功事件；

2. 經過短時間間隔的成功概率必須等于經過長時間間隔的成功概率；

3. 時間間隔趨向于無窮小的時候，一個時間間隔內的成功概率趨近零。

在泊松分布中定義的符號有：

λ是事件的發生率；

t 是事件間隔的長度；

X 是在一個時間間隔內的事件發生次數。

設 X 是一個泊松隨機變量，那么 X 的概率分布稱為泊松分布。以μ表示一個時間間隔 t 內平均事件發生的次數，則 μ=λ*t；

X 的概率分布函數為：

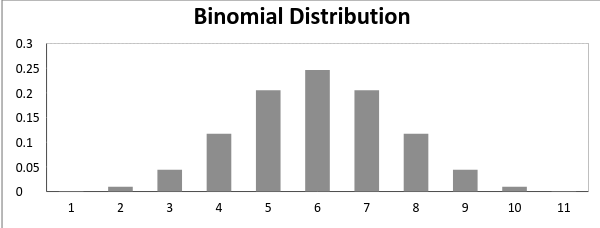
泊松分布的概率分布圖示如下，其中μ為泊松分布的參數：

下圖展示了均值增加時的分布曲線的變化情況：

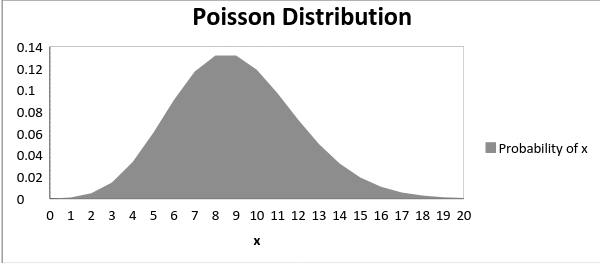
如上所示，當均值增加時，曲線向右移動。泊松分布的均值和方差為：

均值：E(X) = μ

方差：Var(X) = μ

均勻分布

假設我們在從 a 到 b 的一段線段上等距地選擇一個區間的概率是相等的，那么概率在整個區間 [a,b] 上是均勻分布的，概率密度函數也不會隨著變量的更改而更改。均勻分布和伯努利分布不同，隨機變量的取值都是等概率的，因此概率密度就可以表達為區間長度分之一，如果我們取隨機變量一半的可能值，那么其出現的概率就為 1/2。

假定隨機變量 X 服從均勻分布，那么概率密度函數為：

均勻分布曲線圖如下所示，其中概率密度曲線下面積為隨機變量發生的概率：

我們可以看到均勻分布的概率分布圖呈現為一個矩形，這也就是均勻分布又稱為矩形分布的原因。在均勻分布中，a 和 b 都為參數，也即隨機變量的取值范圍。

服從均勻分布的隨機變量 X 也有均值和方差，它的均值為 E(X) = (a+b)/2，方差為 V(X) = (b-a)^2/12

標準均勻分布的密度函數參數 a 取值為 0，b 取值為 1，因此標準均勻分布的概率密度可以表示為：

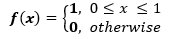
指數分布

現在我們再次考慮電話中心案例，那么電話間隔的分布是怎么樣的呢？這個分布可能就是指數分布，因為指數分布可以對電話的時間間隔進行建模。其它案例可能還有地鐵到達時間的建模和空調設備周期等。

在深度學習中，我們經常會需要一個在 x=0 處取得邊界點 (sharp point) 的分布。為了實現這一目的，我們可以使用指數分布（exponential distribution）：

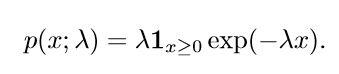
指數分布使用指示函數 (indicator function)1x≥0，以使當 x 取負值時的概率為零。

其中 λ >0 為概率密度函數的參數。隨機變量 X 服從于指數分布，則該變量的均值可表示為 E(X) = 1/λ、方差可以表示為 Var(X) = (1/λ)^2。如下圖所示，若λ較大，則指數分布的曲線下降地更大，若λ較小，則曲線越平坦。如下圖所示：

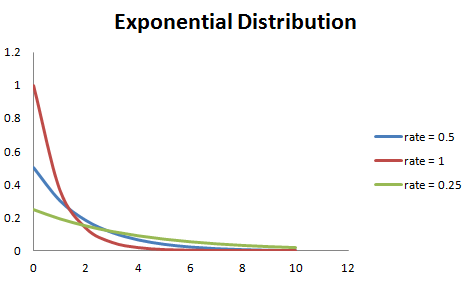
以下是由指數分布函數推導而出的簡單表達式：

P{X≤x} = 1 – exp(-λx)，對應小于 x 的密度函數曲線下面積。

P{X>x} = exp(-λx)，代表大于 x 的概率密度函數曲線下面積。

P{x1

正態分布（高斯分布）

實數上最常用的分布就是正態分布（normal distribution），也稱為高斯分布（Gaussian distribution）。因為該分布的普遍性，尤其是中心極限定理的推廣，一般疊加很多較小的隨機變量都可以擬合為正態分布。正態分布主要有以下幾個特點：

1. 所有的變量服從同一均值、方差和分布模式。

2. 分布曲線為鐘型，并且沿 x=μ對稱。

3. 曲線下面積的和為 1。

4. 該分布左半邊的精確值等于右半邊。

正態分布和伯努利分布有很大的不同，然而當伯努利試驗的次數接近于無窮大時，他們的分布函數基本上是相等的。

若隨機變量 X 服從于正態分布，那么 X 的概率密度可以表示為：

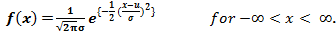
隨機變量 X 的均值可表示為 E(X) = μ、方差可以表示為 Var(X) = σ^2。其中均值μ和標準差σ為高斯分布的參數。

隨機變量 X 服從于正態分布 N (μ, σ)，可以表示為：

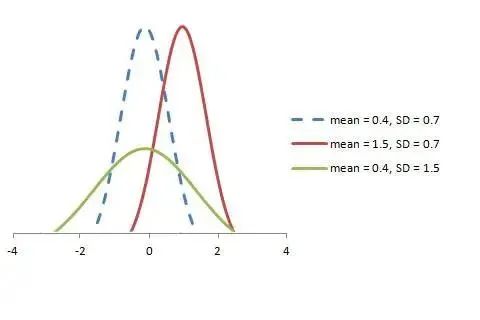
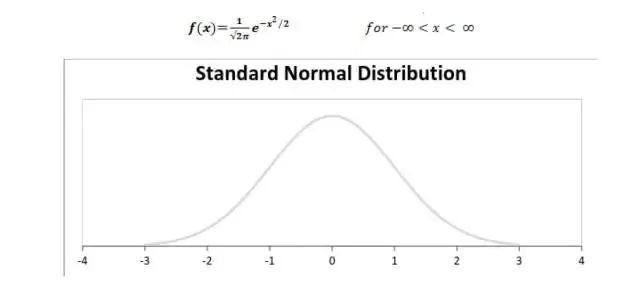
標準正態分布可以定義為均值為 0、方差為 1 的分布函數，以下展示了標準正態分布的概率密度函數和分布圖：

分布之間的關系

伯努利分布和二項分布的關系

1. 二項分布是伯努利分布的單次試驗的特例，即單詞伯努利試驗；

2. 二項分布和伯努利分布的每次試驗都只有兩個可能的結果；

3. 二項分布每次試驗都是互相獨立的，每一次試驗都可以看作一個伯努利分布。

泊松分布和二項分布的關系

以下條件下，泊松分布是二項分布的極限形式：

1. 試驗次數非常大或者趨近無窮，即 n → ∞；

2. 每次試驗的成功概率相同且趨近零，即 p →0；

3.np =λ 是有限值。

正態分布和二項分布的關系 & 正態分布和泊松分布的關系

以下條件下，正態分布是二項分布的一種極限形式：

1. 試驗次數非常大或者趨近無窮，即 n → ∞；

2.p 和 q 都不是無窮小。

參數 λ →∞的時候，正態分布是泊松分布的極限形式。

指數分布和泊松分布的關系

如果隨機事件的時間間隔服從參數為 λ的指數分布，那么在時間周期 t 內事件發生的總次數服從泊松分布，相應的參數為 λt。

測試

讀者可以完成以下簡單的測試，檢查自己對上述概率分布的理解程度：

1. 服從標準正態分布的隨機變量計算公式為：

a. (x+μ) / σ

b. (x-μ) / σ

c. (x-σ) / μ

2. 在伯努利分布中，計算標準差的公式為：

a. p (1 – p)

b. SQRT(p(p – 1))

c. SQRT(p(1 – p))

3. 對于正態分布，均值增大意味著：

a. 曲線向左移

b. 曲線向右移

c. 曲線變平坦

4. 假定電池的生命周期服從 λ = 0.05 指數分布，那么電池的最終使用壽命在 10 小時到 15 小時之間的概率為：

a.0.1341

b.0.1540

c.0.0079

結語

在本文中，我們從最基本的隨機事件及其概念出發討論對概率的理解。隨后我們討論了最基本的概率計算方法與概念，比如條件概率和貝葉斯概率等等。文中還討論了隨機變量的獨立性和條件獨立性。此外，本文更是詳細介紹了概率分布，包括離散型隨機變量分布和連續型隨機變量分布。本文主要討論了基本的概率定理與概念，其實這些內容在我們大學的概率論與數理統計課程中基本上都有詳細的解釋。而對于機器學習來說，理解概率和統計學知識對理解機器學習模型十分重要，以它為基礎我們也能進一步理解結構化概率等新概念。

審核編輯 ：李倩