1. 初始化參數
主要參數:
地圖大小
起始點和目標點坐標
clc clear all m = 30;n = 30; Spoint = [3 3]; %起始點坐標 Epoint = [29 22]; %目標點坐標
2. 構建地圖
-inf表示不可到達的障礙物點
%%構建地圖
for i = 1:m+2
if i == 1
for j = 1:n+2
Matrix(i,j) = -inf;
end
elseif i == m+2
for j = 1:n+2
Matrix(i,j) = -inf;
end
else
for j = 1:n+2
if ((j == 1)|(j == n+2))
Matrix(i,j) = -inf;
else
Matrix(i,j) = inf;
end
end
end
end
%%障礙
for j=2:10
Matrix(5,j)=-inf;
for j=2:15
Matrix(24,j)=-inf;
for j=9:24
%for j=6:24
Matrix(10,j)=-inf;
for j=20:31
Matrix(15,j)=-inf;
for j=5:20
Matrix(20,j)=-inf;
for j=18:27
Matrix(28,j)=-inf;
for i=2:6
Matrix(i,18)=-inf;
for i=17:20
Matrix(i,5)=-inf;
for i=23:25
Matrix(i,20)=-inf;
for i=13:17
Matrix(i,13)=-inf;
end
end
end
end
end
end
end
end
end
end
%end
% 顯示地圖
%subplot(2,2,1);
h1 = plot(Spoint(1),Spoint(2),'gO');
hold on
h2 = plot(Epoint(1),Epoint(2),'rO');
3. A*算法搜索路徑
%%尋路
Matrix(Spoint(1),Spoint(2))=0;
Matrix(Epoint(1),Epoint(2))=inf;
G=Matrix;
F=Matrix;
openlist=Matrix;
closelist=Matrix;
parentx=Matrix;
parenty=Matrix;
openlist(Spoint(1),Spoint(2)) =0;
%closelist(Epoint(1),Epoint(2))=inf;
for i = 1:n+2
for j = 1:m+2
k = Matrix(i,j);
if(k == -inf)
%subplot(2,2,1);
h3 = plot(i,j,'k.');
% elseif(k == inf) % show green feasible point
% %subplot(2,2,1);
% plot(i,j,'gh');
% else
% %subplot(2,2,1);
% plot(i,j,'gh');
end
hold on
end
end
axis([0 m+3 0 n+3]);
%subplot(2,2,1);
plot(Epoint(1),Epoint(2),'b+');
%subplot(2,2,1);
plot(Spoint(1),Spoint(2),'b+');
while(1)
num=inf;
for p=1:m+2
for q=1:n+2
if(openlist(p,q)==0&&closelist(p,q)~=1)
Outpoint=[p,q];
if(F(p,q)>=0&&num>F(p,q))
num=F(p,q);
Nextpoint=[p,q];
end
end
end
end
closelist(Nextpoint(1),Nextpoint(2))=1;
for i = 1:3
for j = 1:3
k = G(Nextpoint(1)-2+i,Nextpoint(2)-2+j);
if(i==2&&j==2|closelist(Nextpoint(1)-2+i,Nextpoint(2)-2+j)==1)
continue;
elseif (k == -inf)
G(Nextpoint(1)-2+i,Nextpoint(2)-2+j) = G(Nextpoint(1)-2+i,Nextpoint(2)-2+j);
closelist(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=1;
elseif (k == inf)
distance=((i-2)^2+(j-2)^2)^0.5;
G(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=G(Nextpoint(1),Nextpoint(2))+distance;
openlist(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=0;
% H=((Nextpoint(1)-2+i-Epoint(1))^2+(Nextpoint(2)-2+j-Epoint(2))^2)^0.5;%歐幾里德距離啟發函數
H_diagonal=min(abs(Nextpoint(1)-2+i-Epoint(1)),abs(Nextpoint(2)-2+j-Epoint(2)));%比較復雜的對角線啟發函數
H_straight=abs(Nextpoint(1)-2+i-Epoint(1))+abs(Nextpoint(2)-2+j-Epoint(2));
H=sqrt(2)*H_diagonal+(H_straight-2*H_diagonal);
% H=max(abs(Nextpoint(1)-2+i-Epoint(1)),abs(Nextpoint(2)-2+j-Epoint(2)));%比較簡單的對角線函數
F(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=G(Nextpoint(1)-2+i,Nextpoint(2)-2+j)+H;
parentx(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=Nextpoint(1);
parenty(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=Nextpoint(2);
else distance=((i-2)^2+(j-2)^2)^0.5;
if(k>(distance+G(Nextpoint(1),Nextpoint(2))))
k=distance+G(Nextpoint(1),Nextpoint(2));
% H=((Nextpoint(1)-2+i-Epoint(1))^2+(Nextpoint(2)-2+j-Epoint(2))^2)^0.5; %歐幾里德距離啟發函數
H_diagonal=min(abs(Nextpoint(1)-2+i-Epoint(1)),abs(Nextpoint(2)-2+j-Epoint(2)));%比較復雜的對角線啟發函數
H_straight=abs(Nextpoint(1)-2+i-Epoint(1))+abs(Nextpoint(2)-2+j-Epoint(2));
H=sqrt(2)*10*H_diagonal+10*(H_straight-2*H_diagonal);
% H=max(abs(Nextpoint(1)-2+i-Epoint(1)),abs(Nextpoint(2)-2+j-Epoint(2)));%比較簡單的對角線函數
F(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=k+H;
parentx(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=Nextpoint(1);
parenty(Nextpoint(1)-2+i,Nextpoint(2)-2+j)=Nextpoint(2);
end
end
if(((Nextpoint(1)-2+i)==Epoint(1)&&(Nextpoint(2)-2+j)==Epoint(2))|num==inf)
parentx(Epoint(1),Epoint(2))=Nextpoint(1);
parenty(Epoint(1),Epoint(2))=Nextpoint(2);
break;
end
end
if(((Nextpoint(1)-2+i)==Epoint(1)&&(Nextpoint(2)-2+j)==Epoint(2))|num==inf)
parentx(Epoint(1),Epoint(2))=Nextpoint(1);
parenty(Epoint(1),Epoint(2))=Nextpoint(2);
break;
end
end
if(((Nextpoint(1)-2+i)==Epoint(1)&&(Nextpoint(2)-2+j)==Epoint(2))|num==inf)
parentx(Epoint(1),Epoint(2))=Nextpoint(1);
parenty(Epoint(1),Epoint(2))=Nextpoint(2);
break;
end
end
P=[];
s=1;
while(1)
if(num==inf)
break;
end
%subplot(2,2,1);
h4 = plot(Epoint(1),Epoint(2),'b+');
P(s,:)=Epoint;
s=s+1;
% pause(1);
xx=Epoint(1);
Epoint(1)=parentx(Epoint(1),Epoint(2));
Epoint(2)=parenty(xx,Epoint(2));
if(parentx(Epoint(1),Epoint(2))==Spoint(1)&&parenty(Epoint(1),Epoint(2))==Spoint(2))
%subplot(2,2,1);
plot(Epoint(1),Epoint(2),'b+');
P(s,:)=Epoint;
break;
end
end
P(s+1,:)=Spoint;
legend([h1,h2,h3,h4],'起始點','目標點','障礙物','航跡點');
count=0;
for i=2:12
for j=2:12
if(G(i,j)~=inf&&G(i,j)~=-inf)
count=count+1;
end
end
end
count
4. 路徑優化
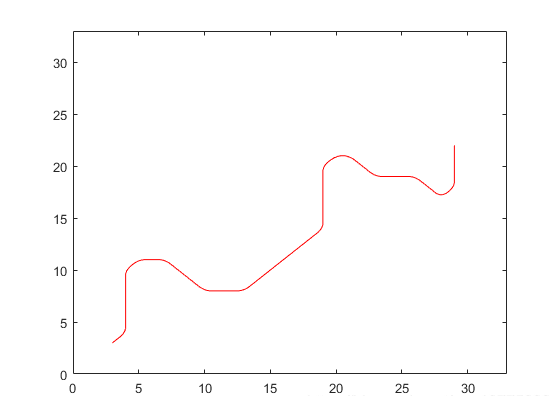
%將得到的折現曲線擬合成光滑的曲線 P=P'; a=[]; b=[]; a=P(1,:); b=P(2,:); figure %subplot(2,2,3); plot(a,b); axis([0,n+3,0,n+3]); values = spcrv([[a(1) a a(end)];[b(1) b b(end)]],3); figure %subplot(2,2,4); plot(values(1,:),values(2,:),'r'); axis([0,m+3,0,m+3]);
5. 效果圖
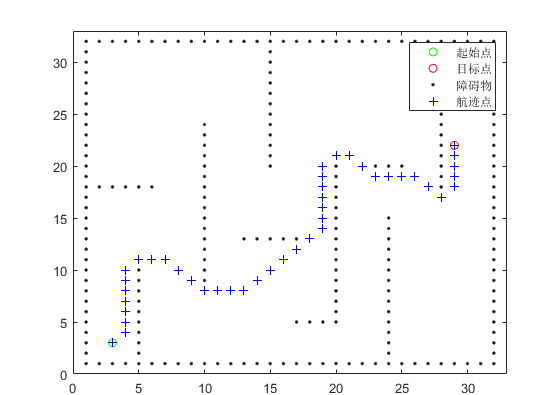
A*路徑
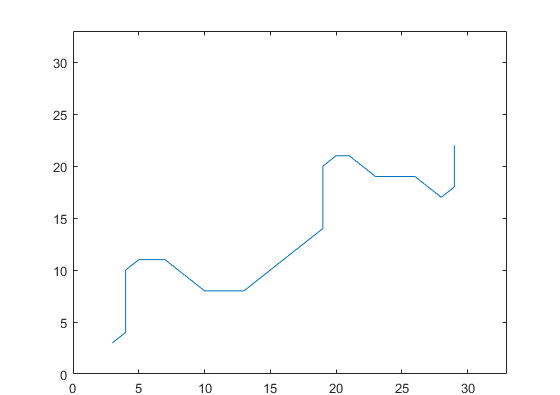
優化后路徑
6. 下載鏈接
直接復制到matlab即可使用,或者也可以點擊下載。
審核編輯:湯梓紅
聲明:本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人,不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用,如有內容侵權或者其他違規問題,請聯系本站處理。
舉報投訴
-
matlab
+關注
關注
189文章
3001瀏覽量
234082 -
算法
+關注
關注
23文章
4709瀏覽量
95339
原文標題:Matlab航跡規劃仿真—A*算法
文章出處:【微信號:3D視覺工坊,微信公眾號:3D視覺工坊】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
熱點推薦
怎么使用Matlab進行電機控制算法仿真?
板,畢竟不是自己的東西,總感覺不得要領,達不到對方波驅動算法那種游刃有余的狀態,看網上很多高手都會用matlab 對電機建模進行Foc 算法仿真,現在疑惑的是
發表于 07-13 18:43
典型雷達航跡的仿真與實現
O 引言在各種雷達訓練和信號模擬器中,都需要進行航跡模擬及航跡顯示,以便于為仿真平臺提供信號源。對于便攜式雷達模擬器來說,無法使用PC,需用嵌入式系統來實現人機交互及信號處理。但當前絕大部分的
發表于 07-10 08:11
基于遺傳算法的PID 控制及其MATLAB 仿真
本 文介紹了遺傳算法和基于遺傳算法的PID 控制設計, 并對設計MATLAB/SIMULINK 下進行了仿真,取得了良好的控制效果。關鍵詞:遺傳算法
發表于 06-11 09:06
?102次下載
多傳感器異步航跡融合算法與仿真
針對分布式多傳感器數據融合系統,提出了一種多傳感器異步航跡融合算法。由于不同傳感器的采樣時間各不相同,融合算法首先利用最小二乘法將局部航跡統一到融合中心的融合
發表于 08-07 09:47
?12次下載
基于半實物仿真系統的多假目標航跡欺騙研究
根據半實物仿真的特點和優點,本文提出了基于半實物仿真系統的多假目標航跡欺騙研究的優勢和價值。然后從實現多假目標航跡欺騙的必要條件、航跡欺騙產
發表于 07-06 16:31
?25次下載
基于改進RRT算法的無人機航跡規劃
為了提高無人機的作戰效率,航跡規劃系統必須為無人機設計出安全系數高,能量消耗少,處理時間短,同時還必須滿足飛行器自身物理特性的威脅回避軌跡。基于上述研究目的,本文
發表于 07-25 11:54
?100次下載
基于模糊聚類的多雷達航跡關聯算法
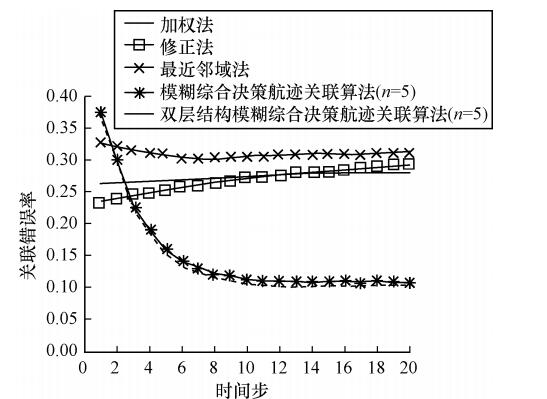
了相似計算與矩陣迭代的次數,最終達到了減小運算量的目的。仿真結果表明:所提算法在保證關聯正確率的前提下,耗時減小了54%,有效地提高了多雷達航跡關聯算法的效率。
發表于 12-18 17:07
?0次下載
一種用于內層規劃的改進粒子群算法
內層規劃的改進粒子群算法,在粒子群算法中引入變異因子,設計了特定的擾動算子,提高了航跡尋優能力。仿真實驗表明,在相同約束的
發表于 12-19 16:01
?0次下載
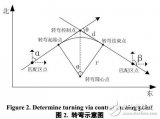
模糊航跡關聯算法的分析及改進
效果變差。為此,研究并改進模糊綜合決策航跡關聯算法,通過引入模糊數學綜合評判中的雙層結構,提出雙層結構模糊綜合決策航跡關聯算法。仿真結果表明
發表于 03-16 10:58
?6次下載





 Matlab航跡規劃仿真—A*算法
Matlab航跡規劃仿真—A*算法













評論