本期內容

上一篇視頻，我們已經對控制系統分析的關鍵 —— 傳遞函數進行了深入淺出的介紹（點我穿越回上一期內容）。

本期視頻則基于前述概念，簡析控制系統的穩定性判據。

01通常，對控制系統的分析主要有兩種思路：

時域分析法

即觀察一段時間內，系統輸出跟隨輸入的響應關系。通常會考慮根據系統的微分方程或傳遞函數、以拉氏變換為數學工具求解，依據響應曲線來分析系統性能。這種方法相對直觀，但數學模型的建立較難。

頻域分析法

轉換思路到頻域進行處理。

因為系統頻率特性可通過實驗測定，并且頻率特性本身也能夠反映系統的傳遞函數，因此在實際操作中頻域分析法對控制系統的分析和設計有著相對更強的實踐意義。 其中圖解法是分析控制系統頻率響應的經典手段，而最為著名的兩種方法就是以奈奎斯特（Nyquist）命名的幅相特性曲線法和以伯德（Bode）命名的對數頻率特性曲線法，二者均通過實驗可測的控制系統開環傳函頻率響應特性來完成對系統穩定性的判斷。

02由于伯德圖在工程實踐中應用更為廣泛，所以今天我們將重點關注如何利用伯德圖對控制系統進行穩定性判斷。

首先，我們在此引入控制系統頻率響應的概念：

即，系統對某一頻率下正弦輸入信號的穩態響應。

圖 ：系統頻率響應說明

分析求解可知，系統的穩態輸出與輸入之間具有同頻、變幅、移相的關系。

而能夠反映上述控制系統（或元件）對不同頻率正弦輸入信號的穩態頻率響應特征的數學模型，即為系統的頻率特性。因為頻率特性屬于傳遞函數的特例，其實質為定義在復平面(s平面)虛軸上的傳遞函數，將它寫為復數形式后，可以看到該復數的模表征了系統的幅頻特性、相角表征了系統的相頻特性：

據此可知，通過向待測系統輸入一個頻率可變的正弦信號，且不斷改變頻率ω的取值，并測量與每一個ω值對應的穩態輸出，記錄相應頻率下穩態輸出與輸入的幅值比和相角差，即可繪制幅值比與相角差隨頻率ω變化的曲線，從而求解幅頻特性與相頻特性表達式，這是一種非常直觀且實踐意義極強的系統特征分析方法。

而伯德提出的對數頻率特性圖解法，是將系統幅頻特性與相頻特性分別畫在兩個對數坐標系中進行分析，由一幅對數幅頻曲線和一幅對數相頻曲線合為完整的對數頻率特性曲線：

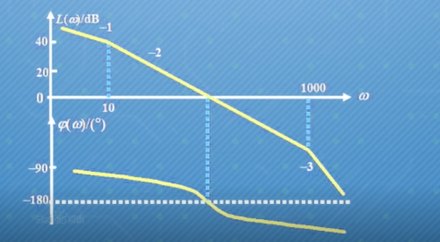
圖 ：對數頻率特性曲線 (伯德圖)

對數頻率特性曲線的橫坐標表示頻率ω，并按對數分度十倍頻程；

對數幅頻曲線L(ω)的縱坐標表示對數幅頻特性的函數值，即20lgA(ω)，線性均勻分度，單位是分貝，即幅頻特性A(ω)每變化十倍，對數幅頻特性L(ω)變化20dB；

對數相頻曲線φ(ω)的縱坐標表示相頻特性的函數值，線性均勻分度，單位是度或弧度。

選擇在對數坐標系內分析，最直觀的好處就是能夠將表示控制系統內環節串聯的幅頻特性乘除運算轉化為對數坐標系內的加減運算，從而簡化曲線繪制；即系統的開環傳遞函數通常可以表示為若干個典型環節相乘形式，實際分析時就可以根據各頻段下起主導作用的典型環節伯德圖來直接完成系統開環伯德圖的繪制。

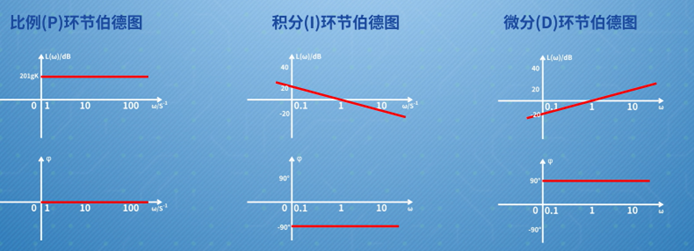
圖 ：控制系統典型環節伯德圖示意

03隨著計算機輔助設計及儀器測量技術的發展，更多情況下，工程師朋友們面臨的往往是根據儀器已經測得的伯德圖來分析系統性能。

其中，頻域性能指標最關鍵的參數就是穩定裕度：

穩定裕度可以定量地表征系統當前距離穩定邊界(臨界穩定)的遠近，是評價系統穩定性好壞的性能指標，也是系統設計的重要依據之一。

良好的穩定裕度可以有效彌補分析設計過程中的簡化處理或實際參數擾動等因素帶來的偏差影響。

那么如何通過伯德圖來判斷系統的穩定裕度呢？

讓我們回到最基本的控制系統判穩條件：系統穩定時，系統所有閉環極點(特征方程的根) 均具有負實部。

這意味著當系統不穩定時，特征方程的根具有正實部，即此時不穩定的閉環系統呈現不收斂的振蕩發散狀態，此時可認為穩態時閉環傳遞函數無窮大，從而可以推導得到系統開環傳遞函數G(s)H(s)=-1。

由此可以繪制開環傳遞函數為-1的系統伯德圖，這就是系統處于臨界穩定的邊界：

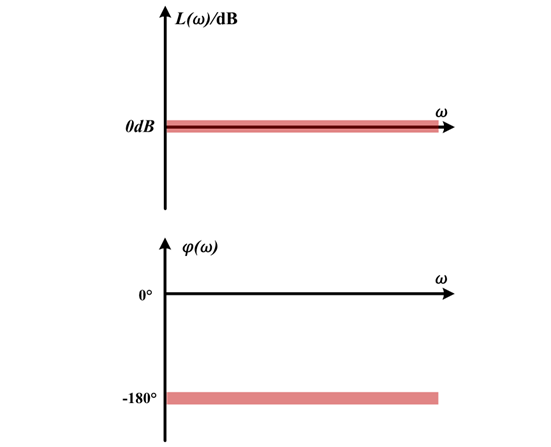
圖 ：系統臨界穩定時的伯德圖

穩定裕度則代表實際控制系統的開環對數頻率特性曲線距離幅頻和相頻穩定邊界的遠近，穩定裕度越高，意味著系統開環對數頻率特性與穩定邊界相去甚遠，則系統抗擾性越好，在真實世界的各種外界擾動下更能實現穩定。

利用伯德圖解法進行開環傳遞函數分析時，需要關注兩個關鍵頻率點：

定義ω_c為開環截止頻率，這一頻率點上系統幅頻響應的幅值增益為1

定義ω_g為相角穿越頻率，這一頻率點上系統相頻響應的相角為-180°

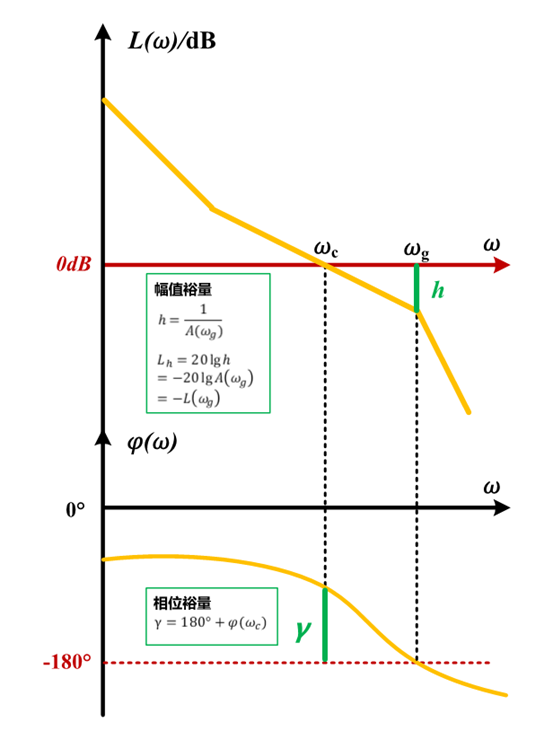
圖 ：相位裕量與幅值裕量的定義

二者即為系統臨界穩定時開環傳函G(s)H(s)=-1所定義的邊界。

定義相位裕量為γ=180°+φ(ω_C)，表征：

此時系統開環幅頻特性不變的情況下，若相頻特性再滯后γ度，系統將觸碰穩定邊界。

定義幅值裕量為h=1/(A(ω_g))，在對數頻率特性坐標系中表示為L_h=20 lg?h=-20lgA(ω_g )=-L(ω_g)，表征：

此時系統開環相頻特性不變的情況下，幅頻特性再增大h倍，系統將觸碰穩定邊界。

一般相位裕量γ>0°理論上即可判斷系統穩定，相位裕量越大則系統穩定程度越高，工程上一般要求設計時γ≥40°；

而幅值裕量h>1、對數幅值裕量L_h≥0dB時也可判斷系統穩定，幅值裕量越大，系統穩定程度越高，類似地，工程上一般會在設計時要求保證L_h≥6dB (6-10dB)。

因此，對于一個控制系統來說，假如它能夠實現在開環幅頻特性穿越0dB線時帶來的相位滯后少于-180°，或開環相頻特性穿越-180°線時其開環幅頻特性已經遠低于0dB線，這樣的對數幅頻特性“穿越”才是表征系統穩定的可靠“穿越”。

04下面，我們來關注伯德圖判穩在電源設計中的實際應用。

BODE100 環路分析儀可以輔助測量電源系統的伯德圖，以MPQ4423C的評估板為例，進行伯德圖的實測：

圖 ：MPQ4423C環路測試示意

24V輸入，5V輸出帶2A負載的情況下，MPQ4423C測得伯德圖如圖所示：

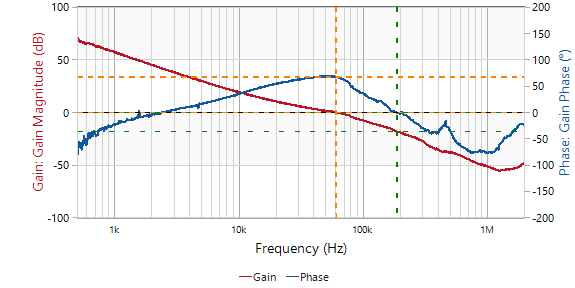
圖 ：EVQ4423C環路測試結果

通過觀察紅色的幅頻特性曲線與0dB線的交截點可以判斷得到MPQ4423C的截止頻率為60kHz； 而開環截止頻率通常有個工程師更為熟悉的名字——帶寬，表征系統的響應速度；帶寬越高，意味著面對動態負載時系統輸出跟隨輸入的響應能力越快。 由于BODE 100環路分析儀在做處理的時候，已將相頻特性曲線整體抬升180°，故通過觀察藍色的相頻特性曲線在截止頻率下距離0°線的距離，即可直接得出系統的相位裕度為67.455°，意味著MPQ4423C有著相當優越的穩定性。 這一期的系統判穩就講到這啦。

下一期我們會和大家探討“環路參數具體該如何調節”，請大家持續關注電源小課堂后續視頻！

審核編輯：湯梓紅