品質因數(Q因數)是一個儲能器件(如電感線圈、電容等)、諧振電路中所儲能量同每周期損耗能量之比的一種質量指標;串聯諧振回路中電抗元件的Q值等于它的電抗與其等效串聯電阻的比值;元件的Q值愈大,用該元件組成的電路或網絡的選擇性愈佳。
Q=無功功率/有功功率
對于無輻射系統,如
Z=R+jX
則Q =|X|/RQ=無功功率/有功功率
串聯諧振回路的品質因數為串聯諧振回路的特性阻抗與回路電阻之比。
在串聯電路中,電路的品質因數Q有兩種測量方法
一是根據公式
Q=UL/U0=Uc/U0測定
Uc與UL分別為諧振時電容器C與電感線圈L上的電壓;
另一種方法是通過測量諧振曲線的通頻帶寬度
△f=f2-f1
再根據
Q=f0/(f2-f1)
求出Q值。
式中f0為諧振頻率,f2與f1是失諧時,亦即輸出電壓的幅度下降到最大值的
1/√2(=0.707)
倍時的上、下頻率點。
Q值越大,曲線越尖銳,通頻帶越窄,電路的選擇性越好。
在恒壓源供電時,電路的品質因數、選擇性與通頻帶只決定于電路本身的參數,與信號源無關。
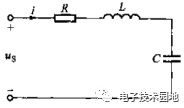
由電容C、電感L和由電容的漏電阻與電感的線電阻R所組成的串聯諧振電路。
此電路的復數阻抗Z為三個元件的復數阻抗之和。
Z=R+jωL+(-j/ωC)=R+j(ωL-1/ωC)(1)
上式電阻R是復數的實部,感抗與容抗之差是復數的虛部,虛部我們稱之為電抗用X表示, ω是外加信號的角頻率。
當X=0時,電路處于諧振狀態,此時感抗和容抗相互抵消了,即式⑴中的虛部為零,于是電路中的阻抗最小。
因此電流最大,電路此時是一個純電阻性負載電路,電路中的電壓與電流同相。
電路在諧振時容抗等于感抗,所以電容和電感上兩端的電壓有效值必然相等,電容上的電壓有效值
UC=I*1/ωC=U/ωCR=QU
品質因數
Q=1/ωCR
這里I是電路的總電流。
電感上的電壓有效值
UL=ωLI=ωL*U/R=QU
品質因數
Q=ωL/R
因為:
UC=UL
所以
Q=1/ωCR=ωL/R
電容上的電壓與外加信號電壓U之比
UC/U=(I*1/ωC)/RI=1/ωCR=Q
電感上的電壓與外加信號電壓U之比
UL/U= ωLI/RI=ωL/R=Q
從上面分析可見,電路的品質因數越高,電感或電容上的電壓比外加電壓越高。
電路的選擇性:
電路的總電流
I=U/Z=U/[R2+(ωL-1/ωC)2]1/2=U/[R2+(ωLω0/ω0-ω0/ωCω0)2]1/2 ω0
是電路諧振時的角頻率。
當電路諧振時有:
ω0L=1/ω0C所以I=U/{R2+[ω0L(ω/ω0-ω0/ω)]2}1/2= U/{R2+[R2(ω0L/R)2](ω/ω0-ω0/ω)2}1/2= U/R[1+Q2(ω/ω0-ω0/ω)2]1/2
因為電路諧振時電路的總電流
I0=U/R
所以
I=I0/[1+Q2(ω/ω0-ω0/ω)2]1/2
有:
I/I0=1/[1+Q2(ω/ω0-ω0/ω)2]1/2
作此式的函數曲線。
設(ω/ω0-ω0/ω)2=Y
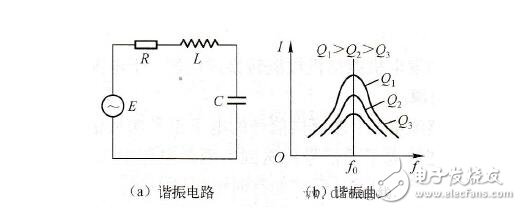
這里會有三條曲線,對應三個不同的Q值,其中有Q1》Q2》Q3。
可看出當外加信號頻率ω偏離電路的諧振頻率ω0時,I/I0均小于1。
Q值越高在一定的頻偏下電流下降得越快,其諧振曲線越尖銳。因此也就是說電路的選擇性是由電路的品質因數Q所決定的,Q值越高選擇性就會越好。
 電子發燒友App
電子發燒友App









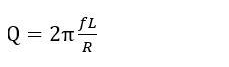


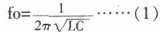










評論