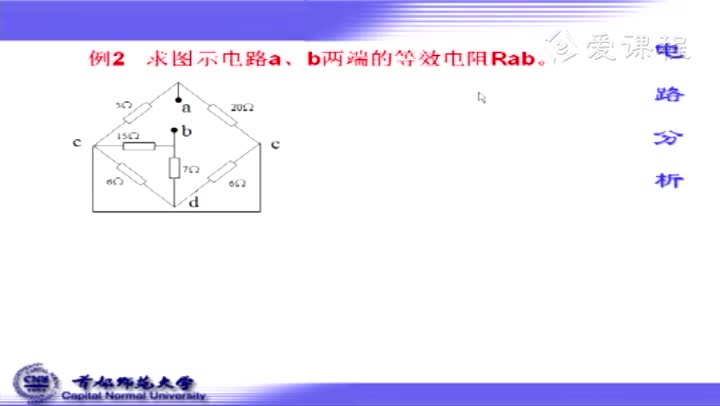
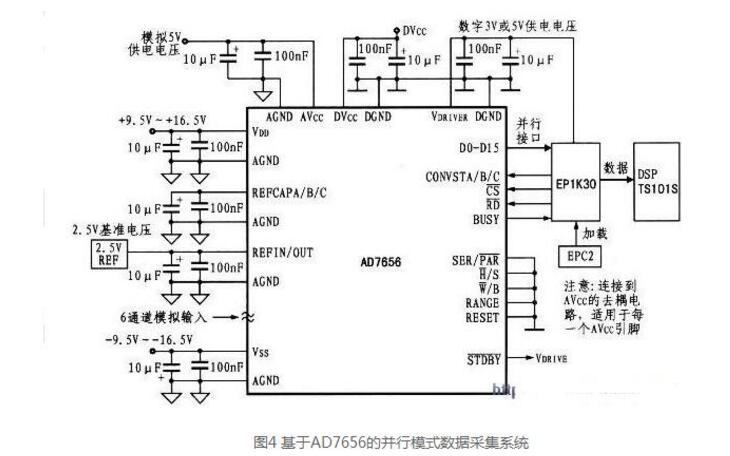
簡單混聯電路分析三:
在如圖所示的電路中,燈泡L標有“6V3W”字樣,電源兩端的電壓和燈絲的電阻均保持不變.當開關S1、S2都斷開時,滑動變阻器R的滑片P從b端滑到某一位置c時(圖中未標出),滑動變阻器R接入電路的電阻減小6Ω,電流表示數變化了0.1A,燈泡恰好正常發光.保持滑動變阻器滑片P的位置不變,閉合開關S1、S2,電流表示數又變化了1.5A.當開關S1、S2都閉合時,調節滑動變阻器滑片P的位置(滑片P不接觸a端),電路消耗的總功率的最小值為20W.
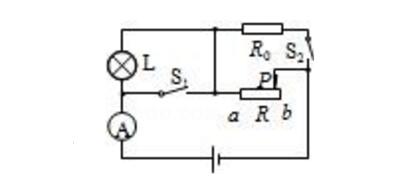
分析:本題有4個過程,畫出每一個過程的電路圖.
(1)當開關S1、S2都斷開時,滑動變阻器在b端時,燈泡L和滑動變阻器的整個電阻Rab串聯在電路中,電路電流為I甲,如圖甲.
(2)當開關S1、S2都斷開時,滑動變阻器R的滑片P從b端滑到某一位置c時,如圖乙.
滑動變阻器Rab接入電路的電阻減小6Ω,電源電壓不變,總電阻減小,電流增大,I乙=I甲+0.1A,此時燈泡正常工作,根據燈泡的額定電壓和額定功率,求出乙圖中的電流.可以求出甲圖中的電流.
根據甲乙兩個過程的電源電壓相等列出等式,求出滑動變阻器的最大阻值Rab、Rac、電源電壓U.
(3)保持滑動變阻器滑片P的位置不變,閉合開關S1、S2,燈泡被短路,R0與Rac并聯,如圖丙,總電阻減小,干路電流增大,干路電流為I丙=I乙+1.5A.由總電壓和總電流求出總電阻,求出R0的電阻.
(4)閉合開關S1、S2,R0與滑動變阻器并聯,要使電路功率最小,電源電壓一定,電路總電流最小,總電阻最大,R0是定值電阻,滑動變阻器連入電路的阻值最大時,電路總電阻最大,如圖丁,求各支路電流,求總電流,求出消耗的最小功率.
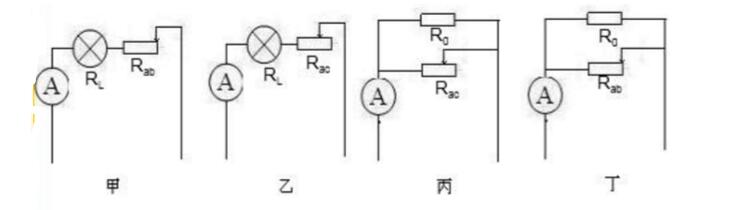
解:甲圖:當開關S1、S2都斷開時,燈泡L和滑動變阻器的整個電阻Rab串聯在電路中,電路電流為I甲.
乙圖:當開關S1、S2都斷開時,滑片滑到c處,燈泡L和滑動變阻器的Rac串聯,電路電阻減小,電流增大,I乙=I甲+0.1A,此時燈泡正常工作:
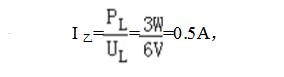
I甲=I乙﹣0.1A=0.5A﹣0.1A=0.4A,燈泡電阻為:

根據甲乙兩個過程電源電壓相等,所以,I甲R甲=I乙R乙,
0.4A×(12Ω+Rab)=0.5A×(12Ω+Rab﹣6Ω),所以,Rab=18Ω,Rac=12Ω,
U=I甲(RL+Rab)=0.4A×(12Ω+18Ω)=12V.
丙圖:保持滑動變阻器滑片P的位置不變,閉合開關S1、S2,燈泡被短路,R0與Rac并聯,總電阻減小,電源電壓不變,總電流增大,I丙=I乙+1.5A=0.5A+1.5A=2A,所以,電路總電阻為:
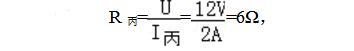
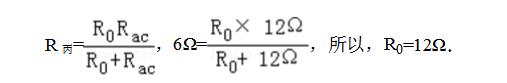
丁圖:當開關S1、S2都閉合時,R0與滑動變阻器并聯,要使總功率最小,電源電壓一定,電路總電流最小,總電阻最大,滑動變阻器電阻最大,電路總電阻最大,所以,R0與Rab并聯。
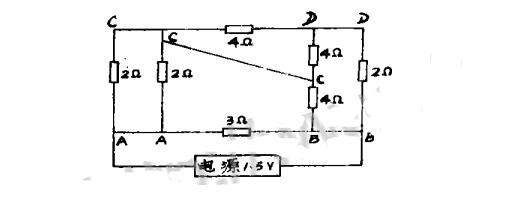
簡單混聯電路分析四:
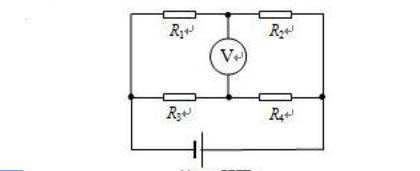
如圖所示的電路中,R1、R2、R3和R4的阻值分別是12歐、18歐、18歐和12歐,電源電壓恒為12伏,電壓表的量程如圖所示的電路中,R1、R2、R3和R4的阻值分別是12歐、18歐、18歐和12歐,電源電壓恒為12伏,電壓表的量程有兩擋:0~3V和0~15V,該電壓表的正確連接應該是?
A.“+”接線柱在上端,量程用0~15V
B.“+”接線柱在上端,量程用0~3V
C.“-”接線柱在上端,量程用0~15V
D.“-”接線柱在上端,量程用0~3V
精解:從電路圖中我們可以把電壓表等效成斷開的導線,那么R1和R2串聯,R3和R4串聯,然后一起并聯到電源兩端,用電勢法,按電流走向從電勢高流向電勢低的規律來看,電流從電源的正極通過外部電流流向電源的負極,得出R2和R4的右端電勢相等,然后電流分別通過R2和R4時電勢各自降低,電勢降低的值就是他們兩端各自的電壓。
U1/U2=R1/R2=12Ω/18Ω=2/3,所以U2=3/5U=7.2V,
又U3/U4=R3/R4=18Ω/12Ω=3/2,所以U4=2/5U=4.8V,所以U4《U2,
即電流通過R4電勢降得少,而R2上電勢降得多,故R4左端電勢高,R2左端電勢低,他們兩端的電勢差(即電壓)為△U=U2-U4=7.2V-4.8V=2.4V《3V.
所以正確答案選D.
 電子發燒友App
電子發燒友App





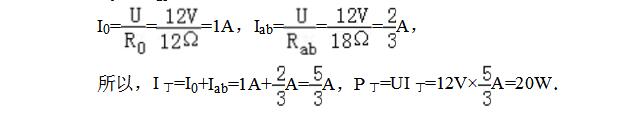






























評論