BLDC電機控制算法

無刷電機屬于自換流型(自我方向轉換)，因此控制起來更加復雜。

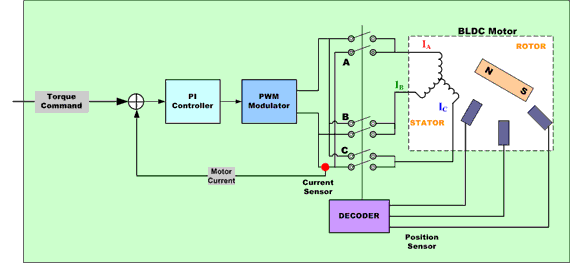
BLDC電機控制要求了解電機進行整流轉向的轉子位置和機制。對于閉環速度控制，有兩個附加要求，即對于轉子速度/或電機電流以及PWM信號進行測量，以控制電機速度功率。

BLDC電機可以根據應用要求采用邊排列或中心排列PWM信號。大多數應用僅要求速度變化操作，將采用6個獨立的邊排列PWM信號。這就提供了最高的分辨率。如果應用要求服務器定位、能耗制動或動力倒轉，推薦使用補充的中心排列PWM信號。為了感應轉子位置，BLDC電機采用霍爾效應傳感器來提供絕對定位感應。這就導致了更多線的使用和更高的成本。無傳感器BLDC控制省去了對于霍爾傳感器的需要，而是采用電機的反電動勢（電動勢）來預測轉子位置。無傳感器控制對于像風扇和泵這樣的低成本變速應用至關重要。在采有BLDC電機時，冰箱和空調壓縮機也需要無傳感器控制。

空載時間的插入和補充

大多數BLDC電機不需要互補的PWM、空載時間插入或空載時間補償。可能會要求這些特性的BLDC應用僅為高性能BLDC伺服電動機、正弦波激勵式BLDC電機、無刷AC、或PC同步電機。

控制算法

許多不同的控制算法都被用以提供對于BLDC電機的控制。典型地，將功率晶體管用作線性穩壓器來控制電機電壓。當驅動高功率電機時，這種方法并不實用。高功率電機必須采用PWM控制，并要求一個微控制器來提供起動和控制功能。

控制算法必須提供下列三項功能：

· 用于控制電機速度的PWM電壓
· 用于對電機進整流換向的機制
· 利用反電動勢或霍爾傳感器來預測轉子位置的方法

脈沖寬度調制僅用于將可變電壓應用到電機繞組。有效電壓與PWM占空度成正比。當得到適當的整流換向時，BLDC的扭矩速度特性與一下直流電機相同。可以用可變電壓來控制電機的速度和可變轉矩。功率晶體管的換向實現了定子中的適當繞組，可根據轉子位置生成最佳的轉矩。在一個BLDC電機中，MCU必須知道轉子的位置并能夠在恰當的時間進行整流換向。

BLDC電機的梯形整流換向

對于直流無刷電機的最簡單的方法之一是采用所謂的梯形整流換向。

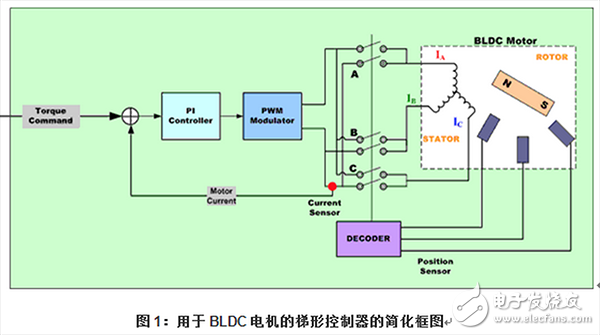
在這個原理圖中，每一次要通過一對電機終端來控制電流，而第三個電機終端總是與電源電子性斷開。

嵌入大電機中的三種霍爾器件用于提供數字信號，它們在60度的扇形區內測量轉子位置，并在電機控制器上提供這些信息。由于每次兩個繞組上的電流量相等，而第三個繞組上的電流為零，這種方法僅能產生具有六個方向共中之一的電流空間矢量。隨著電機的轉向，電機終端的電流在每轉60度時，電開關一次（整流換向），因此電流空間矢量總是在90度相移的最接近30度的位置。

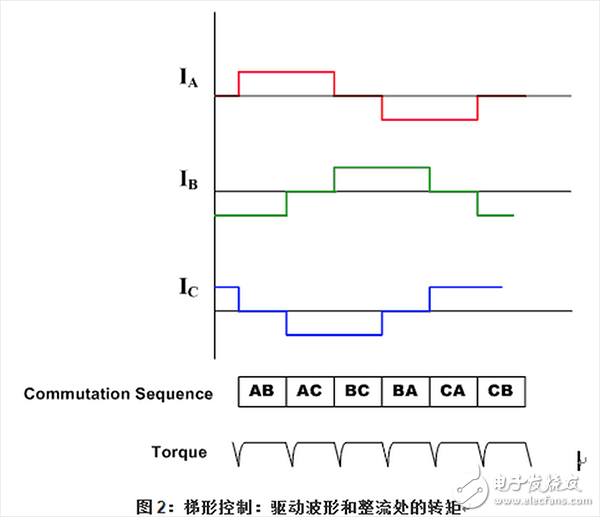
因此每個繞組的電流波型為梯形，從零開始到正電流再到零然后再到負電流。

這就產生了電流空間矢量，當它隨著轉子的旋轉在6個不同的方向上進行步升時，它將接近平衡旋轉。

在像空調和冰霜這樣的電機應用中，采用霍爾傳感器并不是一個不變的選擇。在非聯繞組中感應的反電動勢傳感器可以用來取得相同的結果。這種梯形驅動系統因其控制電路的簡易性而非常普通，但是它們在整流過程中卻要遭遇轉矩紋波問題。

BDLC電機的正弦整流換向

梯形整流換向還不足以為提供平衡、精準的無刷直流電機控制。這主要是因為在一個三相無刷電機（帶有一個正統波反電動勢）中所產生的轉矩由下列等式來定義：

轉軸轉矩= Kt [IR Sin(?) + IS Sin(?+120) + IT Sin(?+240)]

其中

? 為轉軸的電角度
Kt為電機的轉矩常數
IR、IS和IT為相位電流。

如果相位電流是正弦的: IR = I0Sin?; IS = I0Sin (+120?); IT = I0Sin (+240?)將得到

轉軸轉矩 = 1.5I0*Kt (一個獨立于轉軸角度的常數)

正弦整流換向無刷電機控制器努力驅動三個電機繞組，其三路電流隨著電機轉動而平穩的進行正弦變化。選擇這些電流的相關相位，這樣它們將會產生平穩的轉子電流空間矢量，方向是與轉子正交的方向，并具有不變量。這就消除了與北形轉向相關的轉矩紋波和轉向脈沖。

為了隨著電機的旋轉，生成電機電流的平穩的正弦波調制，就要求對于轉子位置有一個精確有測量。霍爾器件僅提供了對于轉子位置的粗略計算，還不足以達到目的要求。基于這個原因，就要求從編碼器或相似器件發出角反饋。

由于繞組電流必須結合產生一個平穩的常量轉子電流空間矢量，而且定子繞組的每個定位相距120度角，因此每個線組的電流必須是正弦的而且相移為120度。采用編碼器中的位置信息來對兩個正弦波進行合成，兩個間的相移為120度。然后，將這些信號乘以轉矩命令，因此正弦波的振幅與所需要的轉矩成正比。結果，兩個正弦波電流命令得到恰當的定相，從而在正交方向產生轉動定子電流空間矢量。

正弦電流命令信號輸出一對在兩個適當的電機繞組中調制電流的P-I控制器。第三個轉子繞組中的電流是受控繞組電流的負和，因此不能被分別控制。每個P-I控制器的輸出被送到一個PWM調制器，然后送到輸出橋和兩個電機終端。應用到第三個電機終端的電壓源于應用到前兩個線組的信號的負數和，適當用于分別間隔120度的三個正弦電壓。結果，實際輸出電流波型精確的跟蹤正弦電流命令信號，所得電流空間矢量平穩轉動，在量上得以穩定并以所需的方向定位。

一般通過梯形整流轉向，不能達到穩定控制的正弦整流轉向結果。然而，由于其在低電機速度下效率很高，在高電機速度下將會分開。這是由于速度提高，電流回流控制器必須跟蹤一個增加頻率的正弦信號。同時，它們必須克服隨著速度提高在振幅和頻率下增加的電機的反電動勢。

由于P-I控制器具有有限增益和頻率響應，對于電流控制回路的時間變量干擾將引起相位滯后和電機電流中的增益誤差，速度越高，誤差越大。這將干擾電流空間矢量相對于轉子的方向，從而引起與正交方向產生位移。當產生這種情況時，通過一定量的電流可以產生較小的轉矩，因此需要更多的電流來保持轉矩。效率降低。隨著速度的增加，這種降低將會延續。在某種程度上，電流的相位位移超過90度。當產生這種情況時，轉矩減至為零。通過正弦的結合，上面這點的速度導致了負轉矩，因此也就無法實現。

AC電機控制算法

標量控制

標量控制（或V/Hz控制）是一個控制指令電機速度的簡單方法，指令電機的穩態模型主要用于獲得技術，因此瞬態性能是不可能實現的。系統不具有電流回路。為了控制電機，三相電源只有在振幅和頻率上變化。

矢量控制或磁場定向控制

在電動機中的轉矩隨著定子和轉子磁場的功能而變化，并且當兩個磁場互相正交時達到峰值。在基于標量的控制中，兩個磁場間的角度顯著變化。

矢量控制設法在AC電機中再次創造正交關系。為了控制轉矩，各自從產生磁通量中生成電流，以實現DC機器的響應性。一個AC指令電機的矢量控制與一個單獨的勵磁DC電機控制相似。在一個DC電機中，由勵磁電流IF所產生的磁場能量Φ F與由電樞電流IA所產生的電樞磁通ΦA正交。這些磁場都經過去耦并且相互間很穩定。因此，當電樞電流受控以控制轉矩時，磁場能量仍保持不受影響，并實現了更快的瞬態響應。三相AC電機的磁場定向控制（FOC）包括模仿DC電機的操作。所有受控變量都通過數學變換，被轉換到DC而非AC。其目標的獨立的控制轉矩和磁通。

磁場定向控制（FOC）有兩種方法：直接FOC: 轉子磁場的方向(Rotor flux angle) 是通過磁通觀測器直接計算得到的間接FOC: 轉子磁場的方向(Rotor flux angle) 是通過對轉子速度和滑差(slip)的估算或測量而間接獲得的。矢量控制要求了解轉子磁通的位置，并可以運用終端電流和電壓（采用AC感應電機的動態模型）的知識，通過高級算法來計算。然而從實現的角度看，對于計算資源的需求是至關重要的。

可以采用不同的方式來實現矢量控制算法。前饋技術、模型估算和自適應控制技術都可用于增強響應和穩定性。

AC電機的矢量控制：

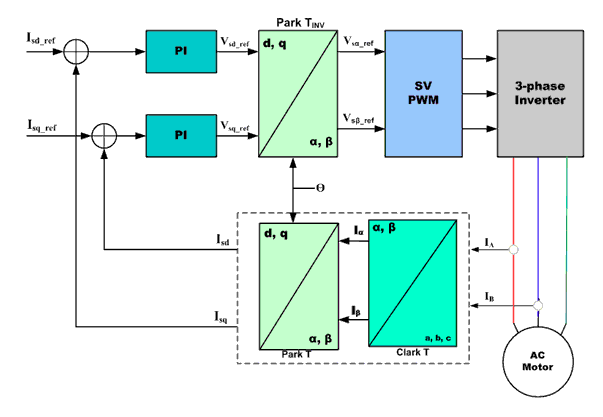
矢量控制算法的核心是兩個重要的轉換: Clark轉換，Park轉換和它們的逆運算。采用Clark和Park轉換，帶來可以控制到轉子區域的轉子電流。這種做充許一個轉子控制系統決定應供應到轉子的電壓，以使動態變化負載下的轉矩最大化

Clark轉換：Clark數學轉換將一個三相系統修改成兩個坐標系統：

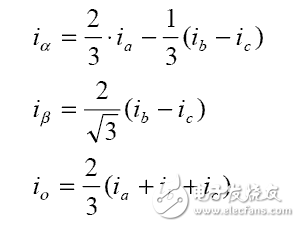
其中Ia和Ib正交基準面的組成部分，Io是不重要的homoplanar部分

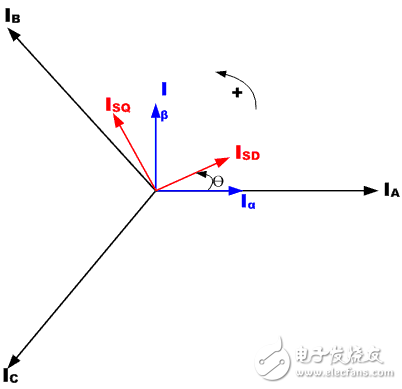
Park轉換：Park數學轉換將雙向靜態系統轉換成轉動系統矢量

兩相α, β幀表示通過Clarke轉換進行計算，然后輸入到矢量轉動模塊，它在這里轉動角θ，以符合附著于轉子能量的d, q幀。根據上述公式，實現了角度θ的轉換。

AC電機的磁場定向矢量控制的基本結構

Clarke變換采用三相電流IA, IB 以及 IC，來計算兩相正交定子軸的電流I?和 I?。這兩個在固定座標定子相中的電流被變換成Isd 和Isq，成為Park變換d, q中的元素。其通過電機通量模型來計算的電流Isd, Isq 以及瞬時流量角θ被用來計算交流感應電機的電動扭矩。這些導出值與參考值相互比較，并由PI控制器更新。

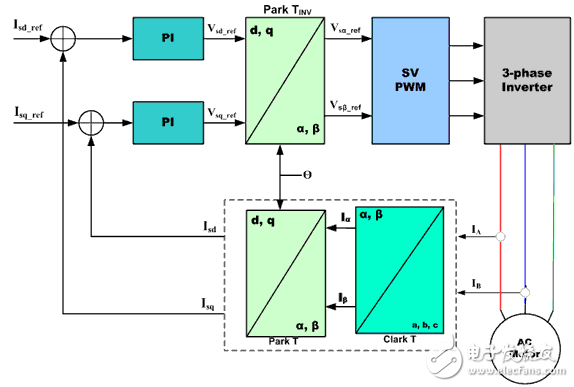
圖2顯示了AC電機磁場定向矢量控制的基本結構。

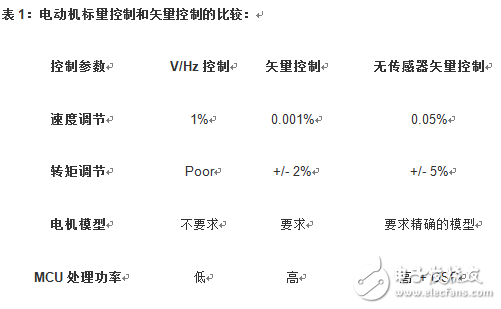
基于矢量的電機控制的一個固有優勢是，可以采用同一原理，選擇適合的數學模型去分別控制各種類型的AC, PM-AC 或者 BLDC電機。

BLDC電機的矢量控制

BLDC電機是磁場定向矢量控制的主要選擇。采用了FOC的無刷電機可以獲得更高的效率，最高效率可以達到95%，并且對電機在高速時也十分有效率。