位置式PID的C語言寫法詳解

　　PID調節口訣：

　　參數整定找最佳，從小到大順序查

　　先是比例后積分，最后再把微分加

　　曲線振蕩很頻繁，比例度盤要放大

　　曲線漂浮繞大灣，比例度盤往小扳

　　曲線偏離回復慢，積分時間往下降

　　曲線波動周期長，積分時間再加長

　　曲線振蕩頻率快，先把微分降下來

　　動差大來波動慢，微分時間應加長

　　理想曲線兩個波，前高后低4比1

　　一看二調多分析，調節質量不會低

　　下面以PID調節器為例，具體說明經驗法的整定步驟：

　　A.、讓調節器參數積分系數S0=0，實際微分系數k=0，控制系統投入閉環運行，由小到大改變比例系數S1，讓擾動信號作階躍變化，觀察控制過程，直到獲得滿意的控制過程為止。

　　B、取比例系數S1為當前的值乘以0.83，由小到大增加積分系數S0，同樣讓擾動信號作階躍變化，直至求得滿意的控制過程。

　　C、積分系數S0保持不變，改變比例系數S1，觀察控制過程有無改善，如有改善則繼續調整，直到滿意為止。否則，將原比例系數S1增大一些，再調整積分系數S0，力求改善控制過程。如此反復試湊，直到找到滿意的比例系數S1和積分系數S0為止。

　　D、引入適當的實際微分系數k和實際微分時間TD，此時可適當增大比例系數S1和積分系數S0。和前述步驟相同，微分時間的整定也需反復調整，直到控制過程滿意為止。

　　PID參數是根據控制對象的慣量來確定的。大慣量如：大烘房的溫度控制，一般P可在10以上，I=3-10，D=1左右。小慣量如：一個小電機帶一臺水泵進行壓力閉環控制，一般只用PI控制。P=1-10，I=0.1-1，D=0，這些要在現場調試時進行修正的。

　　PID參數的設置的大小，一方面是要根據控制對象的具體情況而定；另一方面是經驗。P是解決幅值震蕩，P大了會出現幅值震蕩的幅度大，但震蕩頻率小，系統達到穩定時間長；I是解決動作響應的速度快慢的，I大了響應速度慢，反之則快；D是消除靜態誤差的，一般D設置都比較小，而且對系統影響比較小。對于溫度控制系統P在5-10%之間；I在180-240s之間；D在30以下。對于壓力控制系統P在30-60%之間；I在30-90s之間；D在30以下。

　　這里介紹一種經驗法。這種方法實質上是一種試湊法，它是在生產實踐中總結出來的行之有效的方法，并在現場中得到了廣泛的應用。

　　這種方法的基本程序是先根據運行經驗，確定一組調節器參數，并將系統投入閉環運行，然后人為地加入階躍擾動（如改變調節器的給定值），觀察被調量或調節器輸出的階躍響應曲線。若認為控制質量不滿意，則根據各整定參數對控制過程的影響改變調節器參數。這樣反復試驗，直到滿意為止。

　　經驗法簡單可靠，但需要有一定現場運行經驗，整定時易帶有主觀片面性。當采用PID調節器時，有多個整定參數，反復試湊的次數增多，不易得到最佳整定參數。

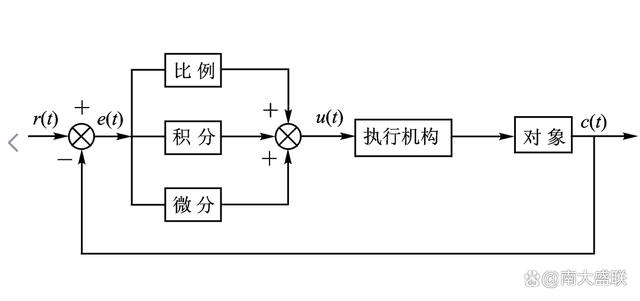
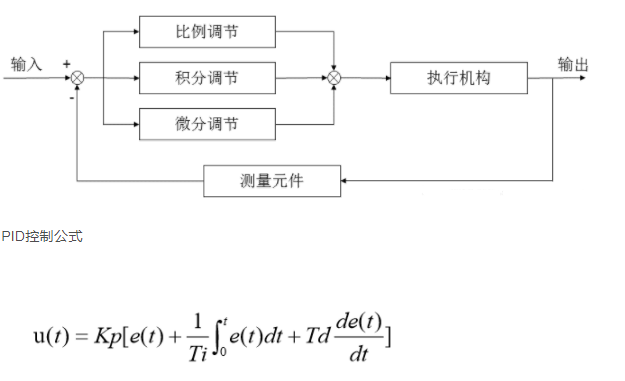
　　PID是比例，積分，微分的縮寫。

　　比例調節作用：是按比例反應系統的偏差，系統一旦出現了偏差，比例調節立即產生調節作用用以減少偏差。比例作用大，可以加快調節，減少誤差，但是過大的比例，使系統的穩定性下降，甚至造成系統的 不穩定。

　　積分調節作用：是使系統消除穩態誤差，提高無差度。因為有誤差，積分調節就進行，直至無差，積分調節停止，積分調節輸出一常值。積分作用的強弱取決與積分時間常數Ti，Ti越小，積分作用就越強。反之Ti大則積分作用弱，加入積分調節可使系統穩定性下降，動態響應變慢。積分作用常與另兩種調節規律結合，組成PI調節器或PID調節器。

　　微分調節作用：微分作用反映系統偏差信號的變化率，具有預見性，能預見偏差變化的趨勢，因此能產生超前的控制作用，在偏差還沒有形成之前，已被微分調節作用消除。因此，可以改善系統的動態性能。在微分時間選擇合適情況下，可以減少超調，減少調節時間。微分作用對噪聲干擾有放大作用，因此過強的加微分調節，對系統抗干擾不利。此外，微分反應的是變化率，而當輸入沒有變化時，微分作用輸出為零。微分作用不能單獨使用，需要與另外兩種調節規律相結合，組成PD或PID控制器。

　　位置式PID算法的C語言代碼

　　typedef struct{

　　float limit; //輸出限幅

　　float target; //目標量

　　float feedback; //反饋量

　　float Kp;

　　float Ki;

　　float Kd;

　　float eSum;

　　float e0; //當前誤差

　　float e1; //上一次誤差

　　}PIDType;

　　#define max（a， b） （a〉b？ a:b）

　　#define min（a， b） （a《b？ a:b）

　　#define range（x， a， b） （min（max（x， a）， b））

　　float pid_pos_update（PIDType *p）

　　{

　　float pe， ie， de;

　　float out=0;

　　//計算當前誤差

　　p-〉e0 = p-〉target - p-〉feedback;

　　//誤差積分

　　p-〉eSum += p-〉e0;

　　//誤差微分

　　de = p-〉e0 - p-〉e1;

　　pe = p-〉e0;

　　ie = p-〉eSum;

　　p-〉e1 = p-〉e0;

　　out = pe*（p-〉Kp） + ie*（p-〉Ki） + de*（p-〉Kd）;

　　//輸出限幅

　　out = range（out， -p-〉limit， p-〉limit）;

　　return out;

　　}