說在前面
1.寫作目的
文章《萌新筆記-天線(原理篇)》介紹了天線分析的基礎(chǔ)理論、常用工程參數(shù)以及常見天線的輻射特性分析,但是沒有針對陣列天線進(jìn)行深入介紹。最近在開展相控陣+載體的一體化仿真研究,其中相控陣的仿真實(shí)現(xiàn)需要依托Matlab-FEKO-API,會涉及到相控陣單元間距、饋電幅度/相位分布計算、波束掃描的實(shí)現(xiàn)等相關(guān)設(shè)計問題,籍此對陣列天線的分析和綜合基礎(chǔ)進(jìn)行了系統(tǒng)學(xué)習(xí)。
2.內(nèi)容涉及
本文的行文邏輯將從以下四個方面展開:
底層認(rèn)知:將通過最通俗易懂的語言對于天線的輻射機(jī)理進(jìn)行描述,幫助讀者建立起對陣列天線輻射機(jī)理最直觀的認(rèn)識;
理論基礎(chǔ):分為直線陣列和平面陣列兩大類,詳細(xì)闡述陣列天線分析理論基礎(chǔ)以及主要的綜合方法。理論基礎(chǔ)的學(xué)習(xí)主要基于陣列天線的學(xué)習(xí)主要依托王建的《陣列天線分析和綜合講義》、薛正輝的《陣列天線分析和綜合》以及諾斯羅普-格魯曼天線工程師布朗的《電掃陣列——MATLAB建模與仿真》三本教材展開:
學(xué)術(shù)前沿:針對一些最新的碩、博論文,進(jìn)行系統(tǒng)學(xué)習(xí),就陣列天線的兩個主要研究方向(陣列綜合算法和陣列天線工程設(shè)計)進(jìn)行開展,基于前面設(shè)計的陣元幅、相分布,完成一個陣列天線的設(shè)計; ?
仿真實(shí)踐:針對陣列天線的相關(guān)應(yīng)用場景,基于仿真軟件HFSS、FEKO,介紹陣列天線幾種實(shí)現(xiàn)方法,仿真實(shí)踐的學(xué)習(xí)主要基于ANSYS和Altair官網(wǎng)培訓(xùn)視頻、幫助文檔以及李明陽、徐興福、謝擁軍所著的HFSS培訓(xùn)教材展開。
底層認(rèn)知
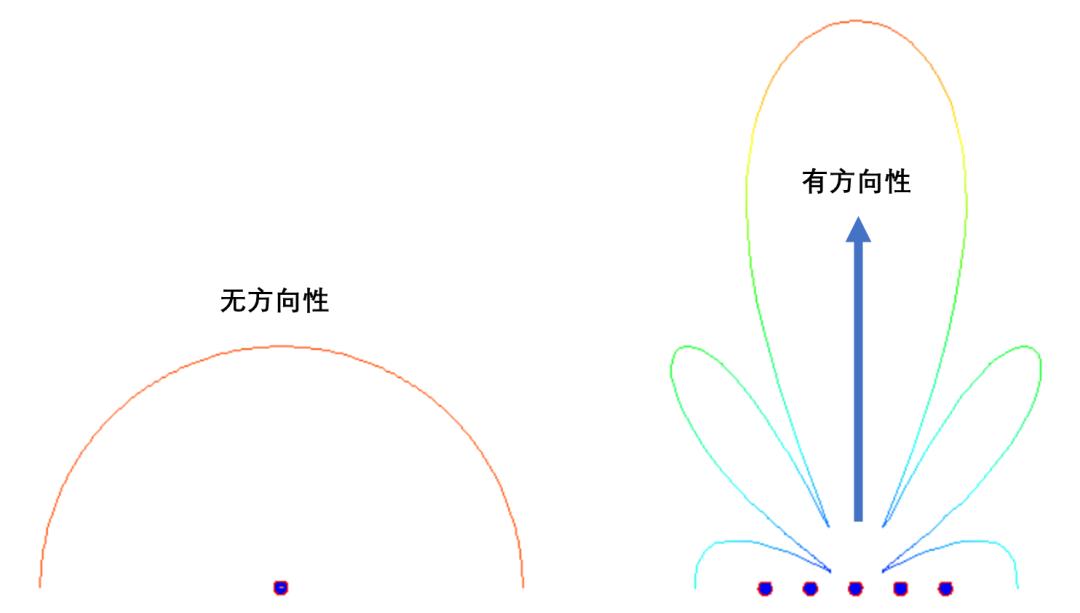
”干涉“和”衍射“是區(qū)別”波“和”粒子“的兩個基本特征,電磁波作為”波“的一種,自然也具備”干涉“和”衍射“現(xiàn)象。其中,所謂”波的干涉“,即具有相同工作頻率的兩個或多個波源所產(chǎn)生的波在空間傳輸?shù)倪^程中,會發(fā)生疊加的現(xiàn)象,從而形成”波峰“和”波谷“交替出現(xiàn)的現(xiàn)象(圖片來自網(wǎng)絡(luò))。
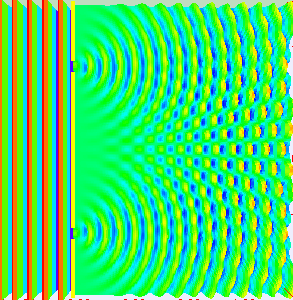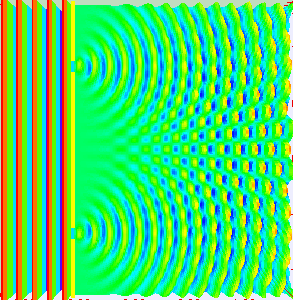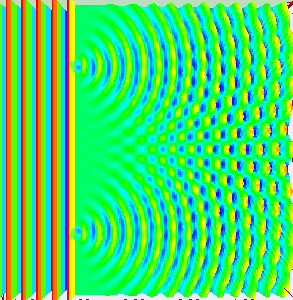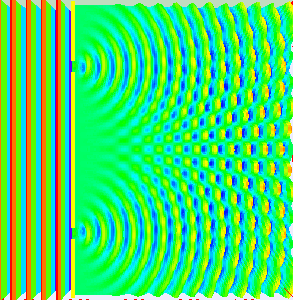
陣列天線的輻射機(jī)理就是大量天線單元輻射的電磁波產(chǎn)生了”干涉“現(xiàn)象,不同天線陣元輻射的電磁波,同相疊加時,產(chǎn)生波瓣,在反相相消的地方,形成零點(diǎn)。如圖所示為含有5個單元的陣列天線的近場和遠(yuǎn)場分布圖像,由由圖可知:一方面電場如同波浪起伏一般由近及遠(yuǎn)的向前傳播,另一方面,不同于單天線的近場分布,陣列天線的電場分布沿周向的分布并不均勻,可以發(fā)現(xiàn)在某些扇區(qū)較亮(場分布同相疊加),而在某些扇區(qū)則較暗(場分布反相相消),從而導(dǎo)致天線陣列的遠(yuǎn)場方向圖表現(xiàn)出明顯的方向性。
?

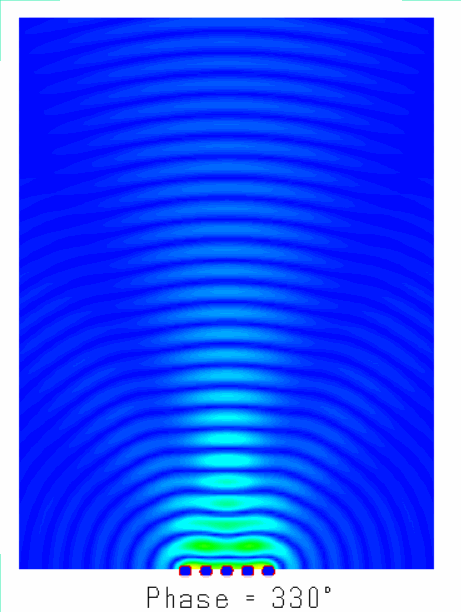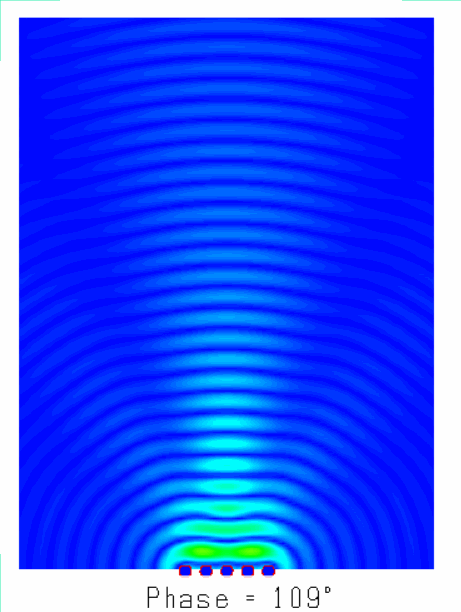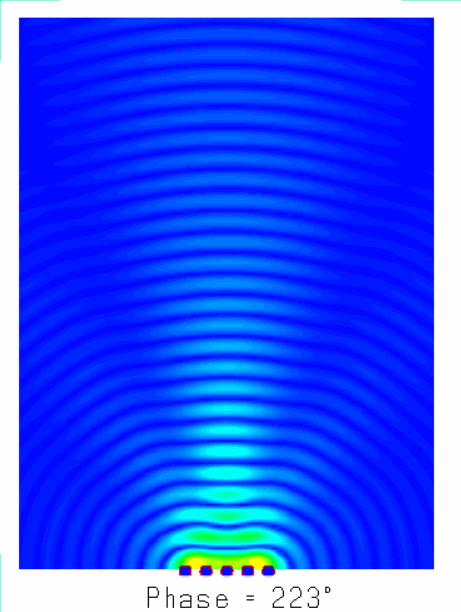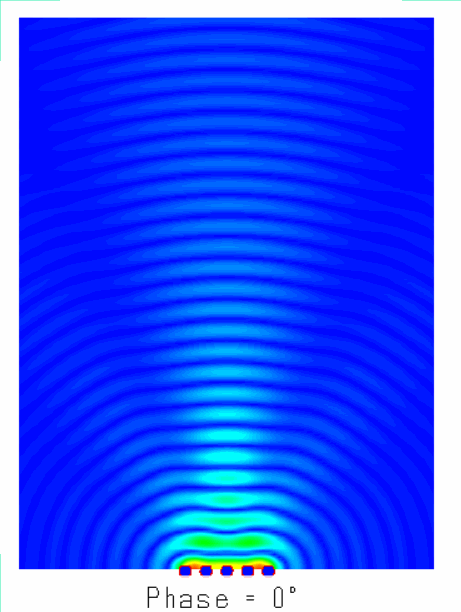
?
?
理論基礎(chǔ)?
1.直線陣列分析與綜合
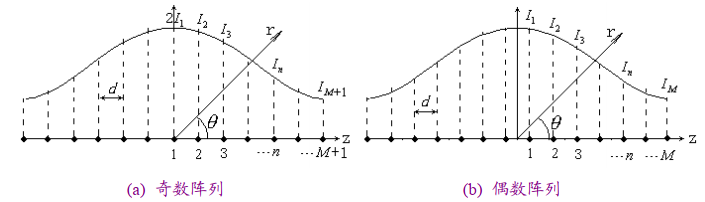
1.1 直線陣列分析
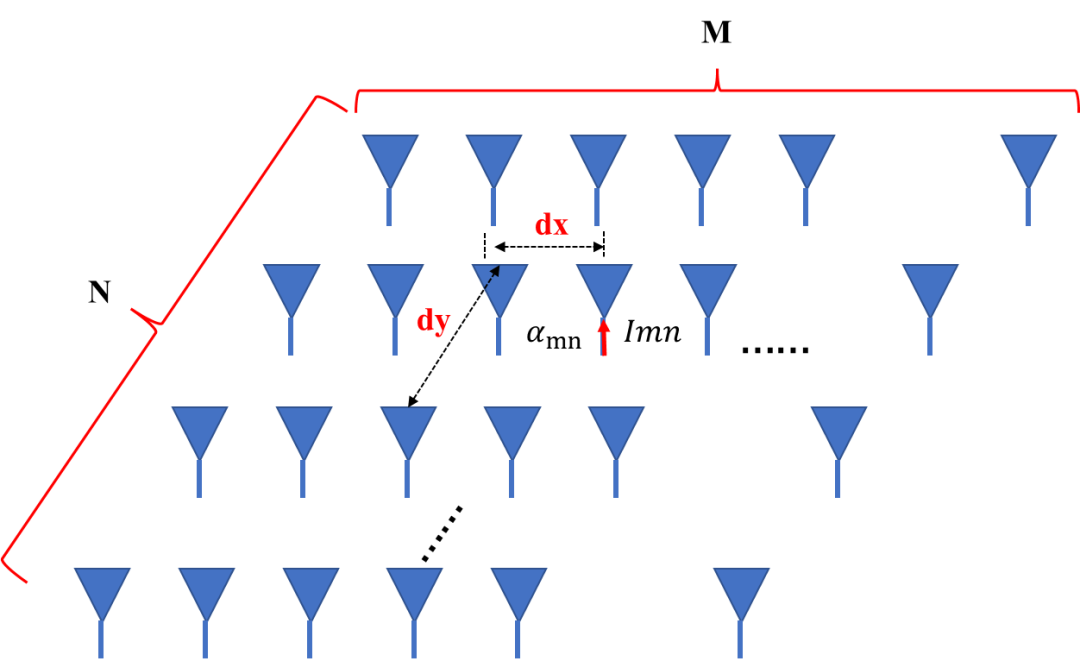
陣列天線性能主要取決于四個參數(shù):
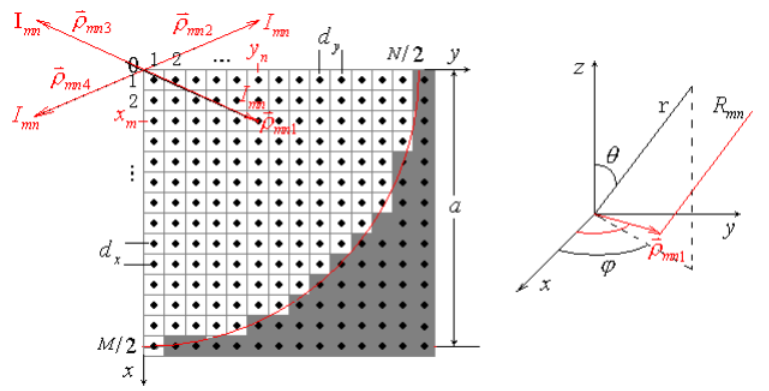
單元總數(shù):如直線陣的N,平面陣的M*N;
單元空間分布(周期):如直線陣的d,平面陣的dx和dy;
單元激勵幅度分布:如直線陣的,平面陣的 ?;
單元激勵相位分布:如直線陣的 ,平面陣的。
電流源的輻射場
正如《萌新筆記—天線(原理篇)》一文中所介紹的,空間中的電/磁場可經(jīng)由輻射體上面的電流分布求得,一般有兩種方法:1)直接法:直接利用格林函數(shù)機(jī)進(jìn)行計算,2)間接法:使用“位函數(shù)”進(jìn)行過渡,先通過輻射體表面電流分布建立“位函數(shù)”的表達(dá)式,再利用“位函數(shù)”計算電磁場分布。
電場分布與磁失位和電標(biāo)位之間的關(guān)系為:
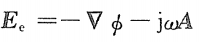
帶入maxwell方程組,即可建立“A”和“”滿足的波動方程:
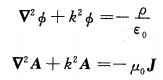
可知,中間變量滿足的波動方程的形式要比“E”和“H”滿足的波動方程的形式簡單很多,由《電磁CAE設(shè)計師的你,有必要了解計算電磁學(xué)嗎?》文章可知,該方程的解可以借助“格林函數(shù)”快速求出:
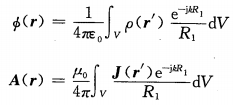
求出中間變量的空間分布后,利用“E”、“H”與中間變量的關(guān)系,即可求解出空間中電磁場的分布。遠(yuǎn)場區(qū):,為小量,近似省略,因此有:
矢量位與“Z軸”平行,遠(yuǎn)場區(qū)電場只有“”方向分量(電場遠(yuǎn)區(qū)封閉,“r”方向分量趨于0):
則有:
其中表示源點(diǎn)的坐標(biāo),R表示源點(diǎn)與場地之間的間距:,帶入電場表達(dá)式,可得:
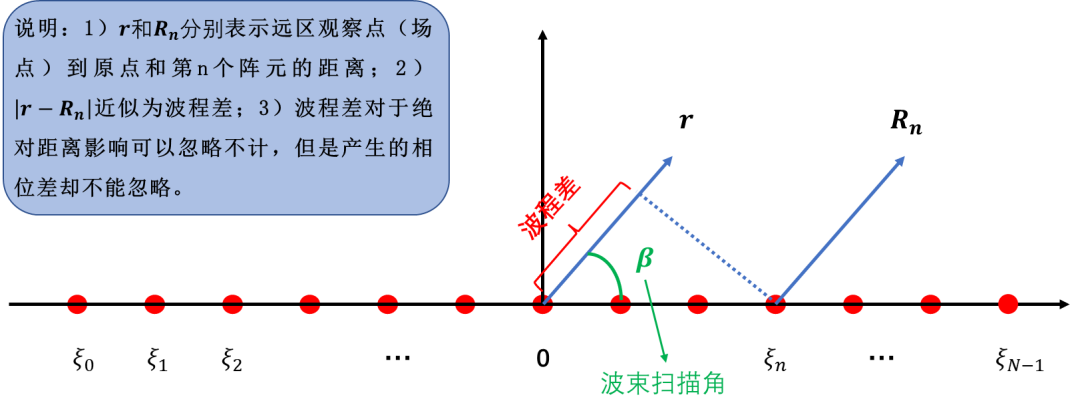
下面以等幅激勵的均勻直線陣列為例,介紹陣列天線的陣因子、波束指向、增益、波束寬度、副瓣電平等主要參數(shù)。
陣因子方向圖?
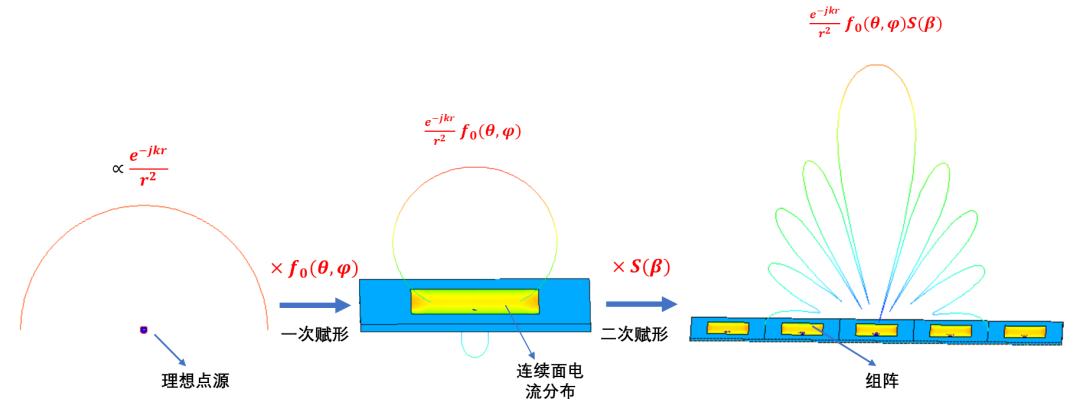
任意形式單元天線的遠(yuǎn)區(qū)輻射場可以統(tǒng)一表示為一下形式:
其中表示每個天線單元的饋電(幅度和相位),表示由于天線電流的分布導(dǎo)致遠(yuǎn)場分布的方向性,即單元方向圖,而則是“格林函數(shù)”項,表示理想點(diǎn)源的遠(yuǎn)場分布形式。三部分共同框定了天線單元對遠(yuǎn)場輻射總場的貢獻(xiàn)。
陣列的輻射總場可以簡單的表示為各天線單元輻射場的疊加,即為:
其中為第n個單元源點(diǎn)與場點(diǎn)的距離:為波程差,即第n個單元源-場距離與原點(diǎn)-場點(diǎn)距離之差,帶入化簡可得:
天線單元的饋電部分可以表示為“復(fù)數(shù)”形式,即為:,則總場可以化簡為:
其中,為陣因子,表示天線單元的組陣給遠(yuǎn)場方向圖帶來的二次賦形。至此,直線陣列天線的遠(yuǎn)場方向圖就算完成了求解,其結(jié)構(gòu)組成也非常清晰,由三部分組成:
第一項為“格林函數(shù)”項,表示理想點(diǎn)源在空間的場分布,其為各向同性的;
因為天線單元表面電流的連續(xù)分布,使得遠(yuǎn)場方向圖被“一次賦形”,“賦形因子 ”即為單元方向圖;
因為單元組陣,使得遠(yuǎn)場方向圖被“二次賦形”,“賦形因子”即為陣列天線的陣因子。
單元相位遞變,因此,饋電幅度,則陣因子可簡化為:
接下來將重點(diǎn)研究因為單元組陣而引起的“二次賦形”,即陣因子。對于均勻直線陣,,利用歐拉公式(詳細(xì)推演見參考教材),陣因子可以化簡為:
其中。?
波束指向?
當(dāng)時,利用無窮小理論,取最大值,為方向圖的主瓣方向,主瓣指向可以利用進(jìn)行確定:
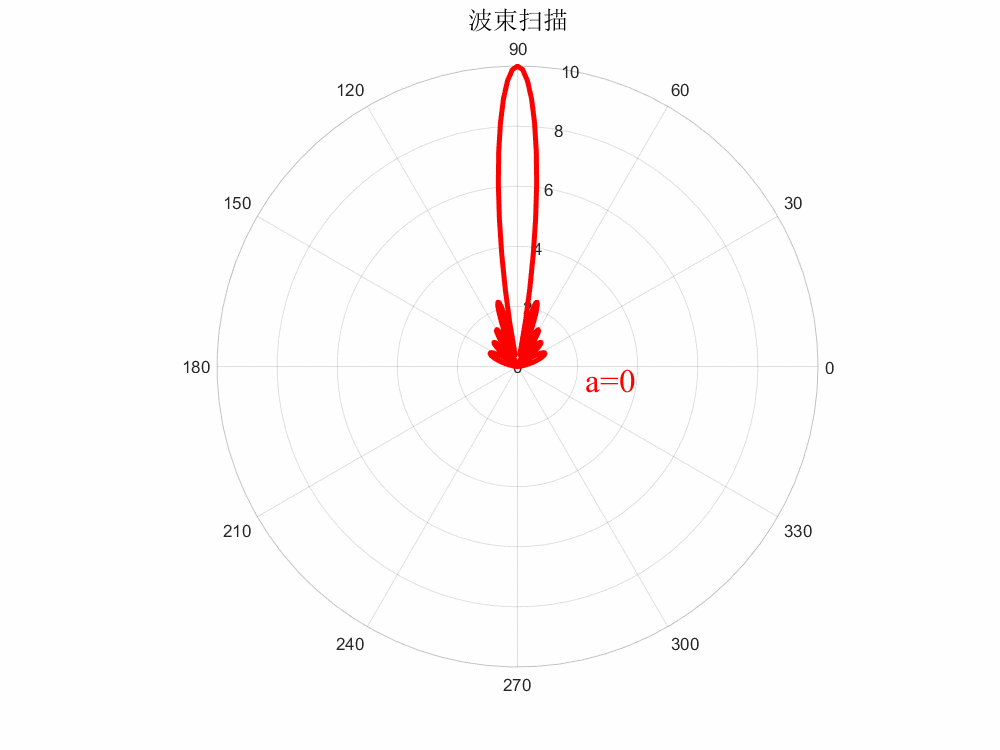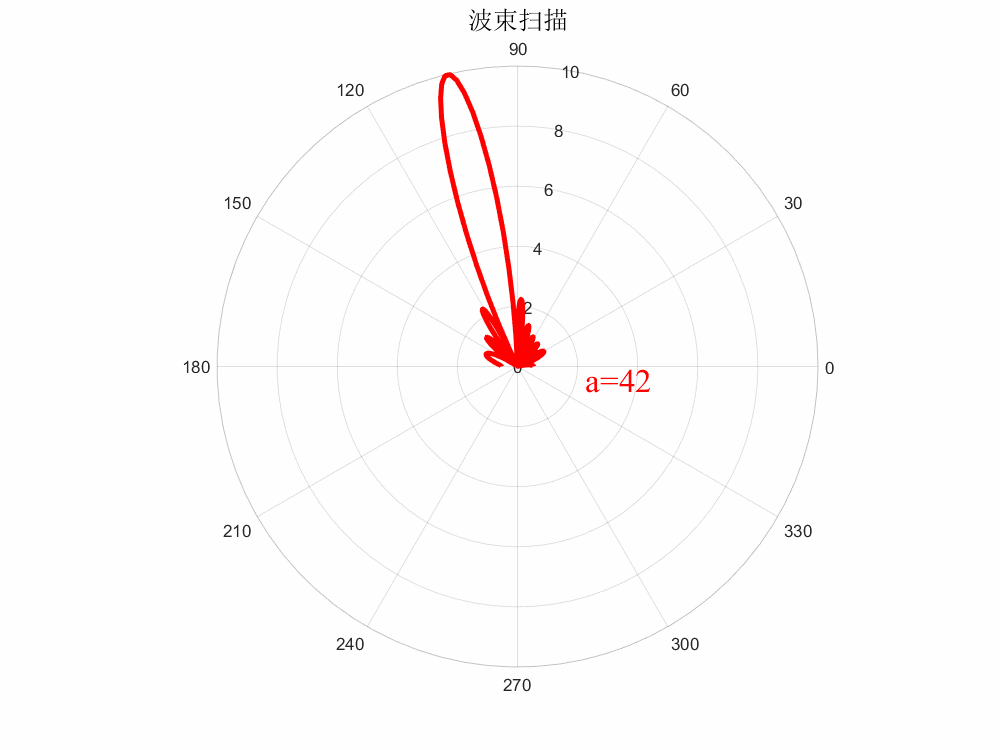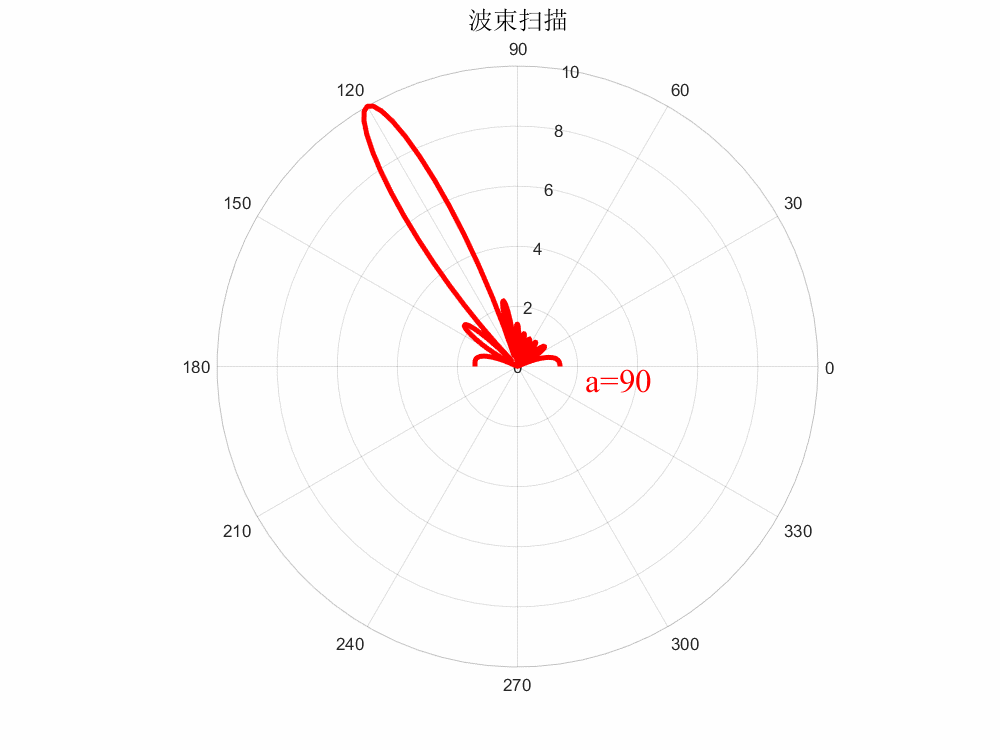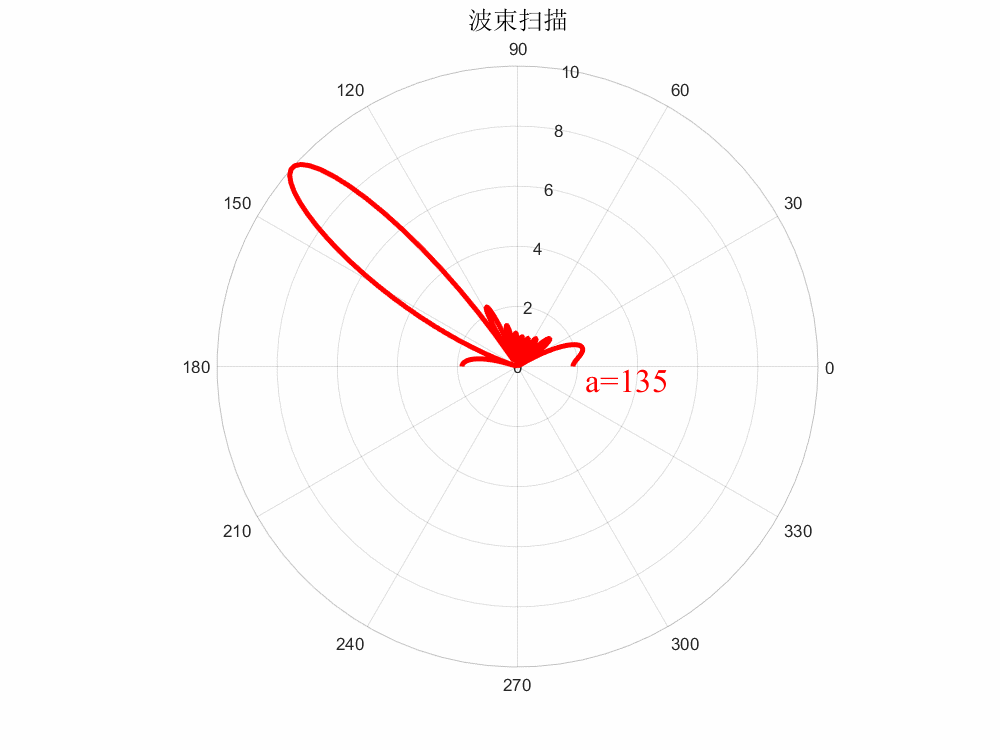
當(dāng)所有單元相位一致時,即,則,波束未掃描;當(dāng)各單元相位均勻遞變時,則波束指向則隨著的變化而進(jìn)行變化,即為相控掃描,這就引出了相掃陣列的一個基本邏輯:
波程差=相位差
?
?
?
?
%?matlab繪制動態(tài)波束掃描(保存GIF格式) clc;clear?all; %%參數(shù)列表 a=0;???????????%相位差 N=10;???????????%陣元數(shù)目 c=3e9;??????????%光速 freq=10e9;??????%工作頻率 lambda=c/freq;??%波長 d=0.5*lambda;???%陣元間距 k=2*pi/lambda;??%波矢 %% x=0180; figure(1); set(gcf,'position',[0,0,800,600],'color','w'); for?i=1:47 ????str_title?=?strcat('color{red}a=',num2str(a)); ????y=abs((sin(N.*(k.*d.*cos(x.*pi./180)+a.*pi./180)/2))./sin((k.*d.*cos(x.*pi./180)+a.*pi./180)/2));%方向圖函數(shù) ????a=(i-1)*360/120;??%相位差掃描范圍 ????figure(i); ???? ????set(gcf,'position',[0,0,800,600],'color','w'); ????p1?=?polarplot(x.*pi./180,y,'r','LineWidth',3); ????hold?on; ????title('波束掃描','fontsize',15); ????text(-0.2,2.3,str_title,'FontName','Times?New?Roman','FontSize',20); ????%%保存為gif格式 ????frame?=?getframe(gcf); ????im?=?frame2im(frame); ????[I,map]?=?rgb2ind(im,256); ????if?i==1 ????????imwrite(I,map,'波束掃描.gif','gif','Loopcount',Inf,'DelayTime',0.05); ????else ????????imwrite(I,map,'波束掃描.gif','gif','WriteMode','append','DelayTime',0.05); ????end ????close(figure(i)); end
主瓣寬度?
天線的主瓣寬度通常指方向圖主瓣增益下降3dB(半功率)時所對應(yīng)的波束寬度,功率下降為原來的0.5倍,則電場幅值下降為原來的0.707倍(),即有歸一化陣因子:
=0.707
其中,對于側(cè)射陣(端射狀態(tài)詳見教材),主瓣指向,經(jīng)過化簡計算,可得波束寬度:
為波束掃描角。可見:1)陣列單元數(shù)目N越大,波束越窄;2)掃描角度(相對側(cè)射狀態(tài))越大,波束越寬,利用該公式可以在陣列設(shè)計之初,對天線陣列的波束寬度進(jìn)行估計。
方向性系數(shù)D?
均勻直線陣的方向性系數(shù)D定義為主瓣最大方向的功率密度與平均功率密度之比,可以由如下公式進(jìn)行計算:
其中為歸一化陣因子,,對進(jìn)行計算,可得:
則方向性系數(shù)D為:
其中為陣列長度(口徑)。
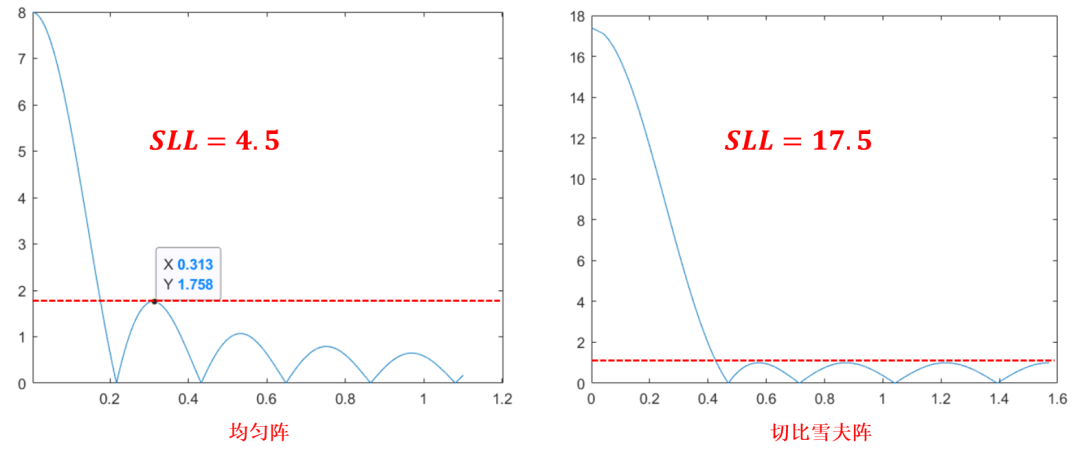
副瓣電平?
副瓣電平為天線的重要技術(shù)指標(biāo),乃至于后續(xù)天線綜合的主要工作就是圍繞著副瓣電平SLL的優(yōu)化而開展的。其定義為最大副瓣與主瓣之比,即:
對于均勻直線陣,第一副瓣即為最大副瓣,此時,其中,帶入公式,可以算的:
=-13.5dB
即均勻直線陣的副瓣電平并不是特別優(yōu)秀,想要獲得更低的副瓣電平,還需要進(jìn)一步對陣列單元的饋電幅度進(jìn)行一定的設(shè)計,這就是“陣列綜合”的知識了。
柵瓣抑制?
由上文可知,均勻陣線陣列的陣因子為:
為周期函數(shù)(周期為,取絕對值后周期為周期為),即與主瓣等高的波瓣會每隔出現(xiàn)一次。
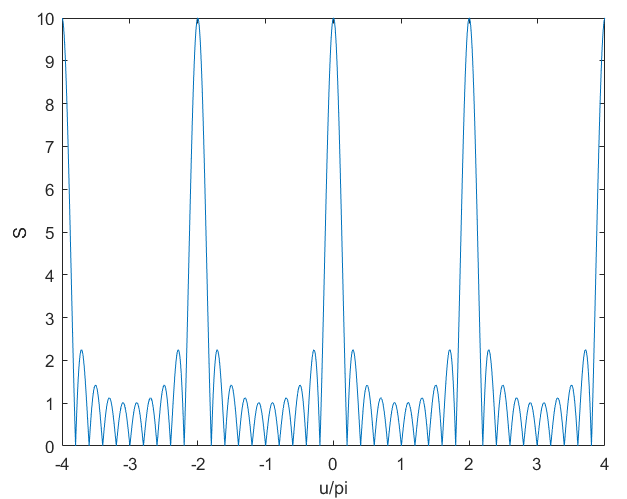
因此要抑制柵瓣的出現(xiàn),就需要對u的取值范圍,即,化簡可得:
此即為均勻直線陣的柵瓣抑制條件。
1)對于側(cè)射陣:,則有;?
2)當(dāng)波束掃描時,按掃角計算,則取,
,一般取
1.2 直線陣列綜合?
等幅激勵直線陣的副瓣電平太高,無法滿足工程上的使用要求,因此提出兩種陣列綜合的方法,目標(biāo)是降低天線的副瓣電平。陣列綜合方式:已知方向圖參數(shù)(副瓣電平等),求解陣元的電流分布(幅度+相位),最主要的的是求電流的幅度分布,相位分布依據(jù)波束指向,根據(jù)“相位差=波程差”的原則進(jìn)行計算,與綜合方法無關(guān)。
其中之一為切比雪夫綜合法,該綜合法是一種等副瓣的綜合方法,其特點(diǎn)為:
等副瓣電平;
在相同副瓣電平和相同陣列長度下主瓣最窄,在主瓣寬度一定的情況下旁瓣最低,為最佳陣列;
單元數(shù)多(N>13)時,陣列兩端單元激勵幅度跳變大,使饋電困難。
為了防止讀者陷入浩瀚 的公式推演而迷失方向,先介紹一下“切比雪夫綜合“的實(shí)現(xiàn)思路:1)第一步就是基于切比雪夫多項式建立一個目標(biāo)方向圖表達(dá)式;2)第二步就是計算N元陣的方向圖表達(dá)式,并令其與目標(biāo)方向圖相等,從而計算出陣元幅度分布。
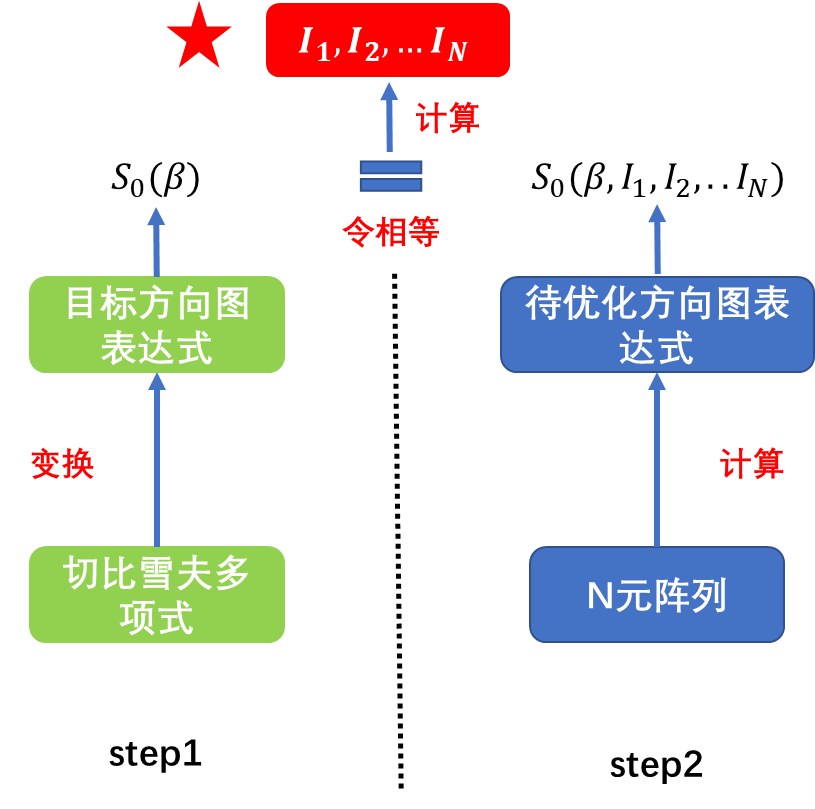
切比雪夫多項式
切比雪夫多項式為如下二階微分方程的解:
令
則上式可化簡為:
方程的一個解為:? 同時,基于三角恒式:? 可得切比雪夫多項式的遞推關(guān)系式:? 利用遞推關(guān)系式可計算得到任意階切比雪夫函數(shù)的“多項式”表達(dá)形式:
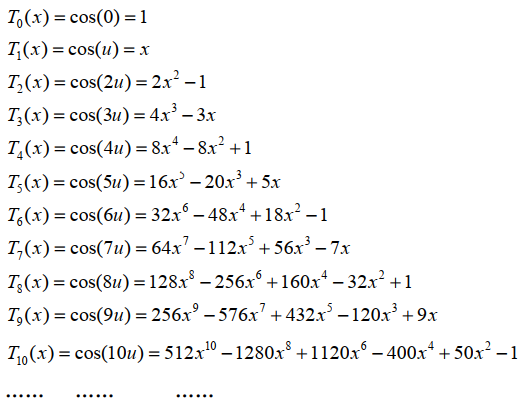
上面為的函數(shù)形式,當(dāng)時,則變成雙曲余弦的形式,整合下來,切比雪夫函數(shù)的“三角函數(shù)”表達(dá)形式為:
利用matlab作圖可以畫出任意階切比雪夫函數(shù)曲線如下圖所示,由圖可知當(dāng)時,切比雪夫多項式為振幅為1的振蕩曲線,當(dāng)時,曲線快速上升,若將作為方向圖主瓣位置,將區(qū)域作為方向圖的副瓣區(qū)域,則可以實(shí)現(xiàn)方向圖的副瓣電平SLL的調(diào)節(jié)。
clc;clear?all;close?all; x=-1.11.1; y=zeros(1,length(x)); for?m=15 ????for?i=1:length(x) ????if?abs(x(i))<1 ????????y(i)=cos(m*acos(x(i))); ????elseif?abs(x(i))>=1 ????????y(i)=cosh(m*acosh(x(i)));? ????end end plot(x,y); hold?on; end
?
?
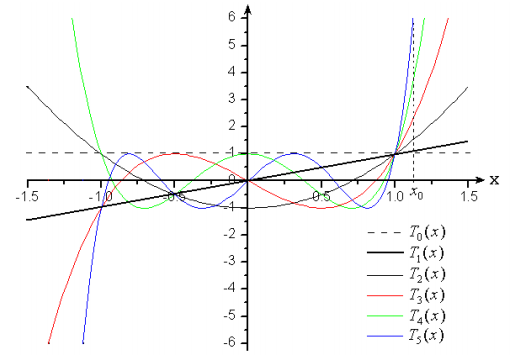
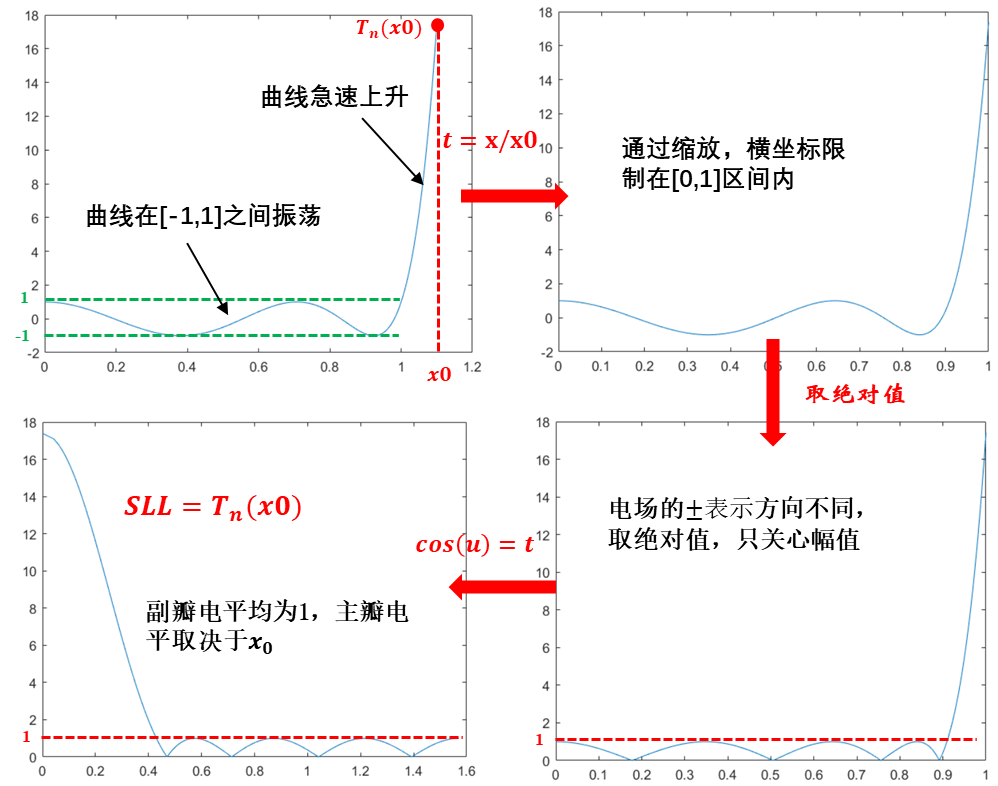
乍一看,曲線很亂,很難將其與陣因子方向圖聯(lián)系起來,現(xiàn)在我們嘗試通過一系列變換建立其與方向圖的聯(lián)系(取n=8,函數(shù)曲線取坐標(biāo)系的正半邊進(jìn)行考察),變換過程如下:
取的切比雪夫多項式進(jìn)行研究,由圖可知時,曲線在內(nèi)振蕩,的位置決定了的高度,曲線如圖1所示;
令,將曲線定義域收縮至[0,1];
對表達(dá)式取絕對值,即忽略電場方向帶來的“正負(fù)”,統(tǒng)一考察電場幅值大小;
令,會發(fā)現(xiàn)原本的函數(shù)曲線竟然神奇變成了我們熟悉的方向圖。由圖可知:1)該方向圖所有副瓣均相等(等副瓣);2)副瓣電平始終為1,主瓣電平為,主副瓣比SLL的大小取決于最初選擇的的大小,即主副瓣比可調(diào)。
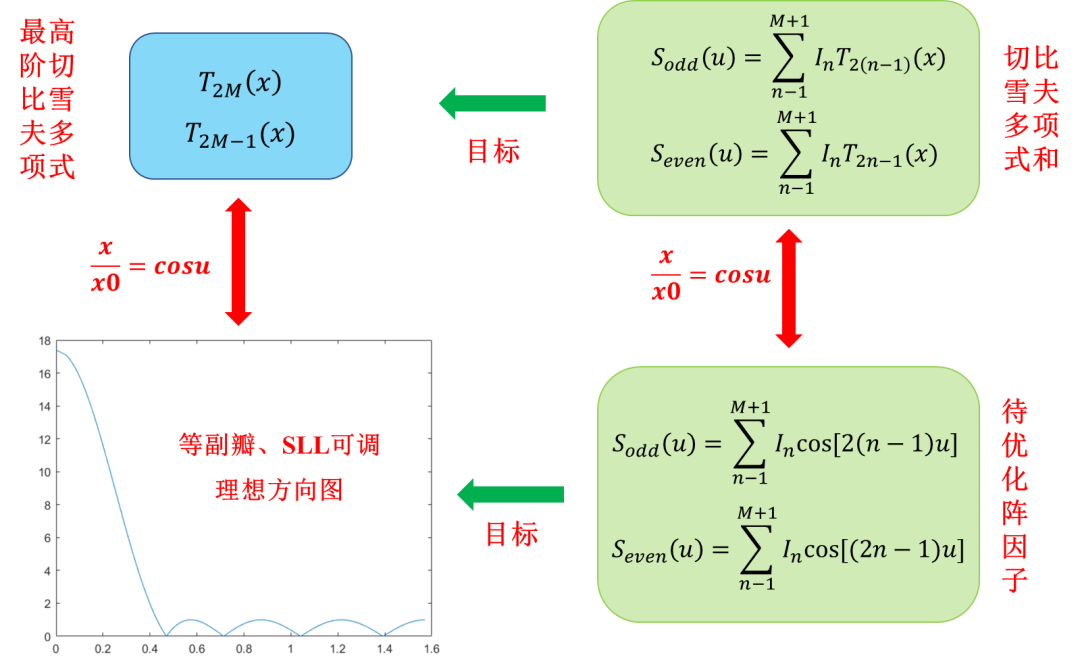
?切比雪夫綜合?
由上面可知,經(jīng)由切比雪夫多項式,通過適當(dāng)?shù)淖儞Q,就可以得到主副瓣比可調(diào)的等副瓣方向圖,下面就需要建立目標(biāo)陣因子和切比雪夫函數(shù)的關(guān)系,以期實(shí)現(xiàn)相同的方向圖分布特性。非等幅的直線陣列的的陣因子為:
設(shè)饋電幅度為對稱分布,按照陣元數(shù)目的奇偶,依據(jù)歐拉公式,對稱位置兩兩相消,陣因子可以化簡為:
當(dāng)均取1時(即為等幅),計算可得其SLL明顯小于切比雪夫陣:
如果令:
我們就會發(fā)現(xiàn)陣因子中的每一項都是一個切比雪夫多項式,其中:
因此陣因子表達(dá)式即為一系列切比雪夫多項式的和:
總結(jié)下來,切比雪夫陣的設(shè)計思路為:如果希望待優(yōu)化陣因子變成理想方向圖,那么就需要令其等價的切比雪夫多項式之和與相應(yīng)最高階切比雪夫多項函數(shù)相等,從而求出陣列饋電幅度分布{......}。同時,通過的調(diào)節(jié),即可實(shí)現(xiàn)方向圖副瓣電頻SLL的調(diào)節(jié)。
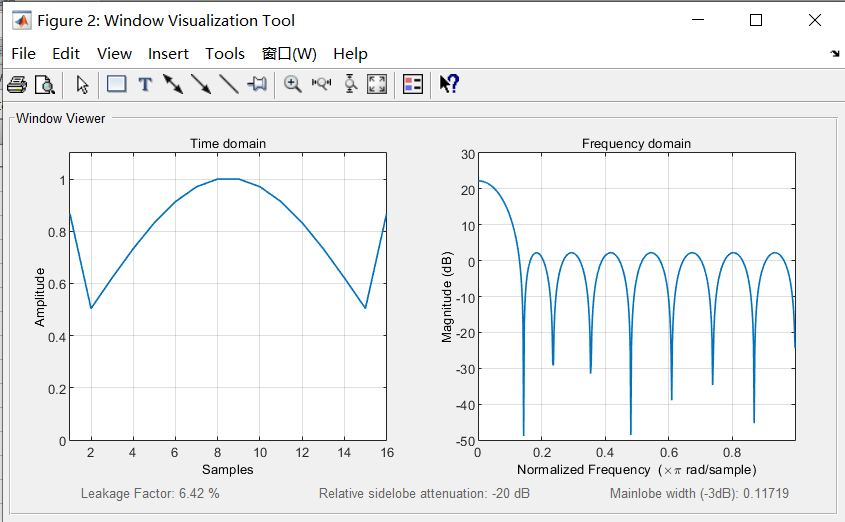
實(shí)際工程中,無需手動計算出切比雪夫綜合的陣元分布,利用MATLAB自帶的函數(shù)即可輕松完成計算。
N=16;%陣元數(shù)目 SLL=20;%副瓣電平 w = chebwin(N,SLL);%輸出陣元幅度分布 wvtool(w);%查看陣元幅度分布及方向圖預(yù)覽
?
?
泰勒綜合法?
當(dāng)陣列單元數(shù)目較多(),切比雪夫陣列兩端單元的激勵幅度將發(fā)生跳變,即最末單元比其相鄰單元的激勵幅度大許多,不利于饋電并對方向圖副瓣電平影響很大,此時需要引入泰勒綜合法。
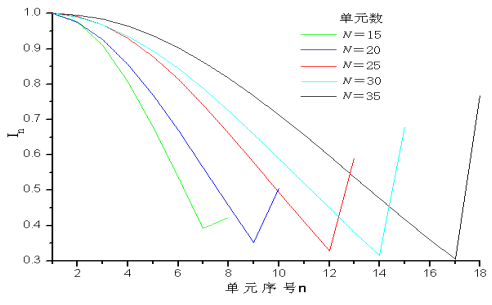
采用泰勒綜合方法設(shè)計的泰勒陣列,其方向圖只是靠近主瓣某個區(qū)域內(nèi)的副瓣電平接近相等,隨后單調(diào)減小,有利于提高天線的方向性,且激勵的幅度分布的變化在陣列兩端是單調(diào)減小的,不會出現(xiàn)兩端單元激勵幅度跳變的情況。
與”切比雪夫綜合“類似,”泰勒綜合“的思路也大致分為兩步:1)依據(jù)切比雪夫多項式,結(jié)合理想線源函數(shù),通過變換,構(gòu)建目標(biāo)方向圖(泰勒函數(shù));2)計算連續(xù)線源的方向圖表達(dá)式,并令其等于目標(biāo)方向圖,從而計算出”連續(xù)線源“的分布,在對其離散,即得到N元陣列的幅度分布。
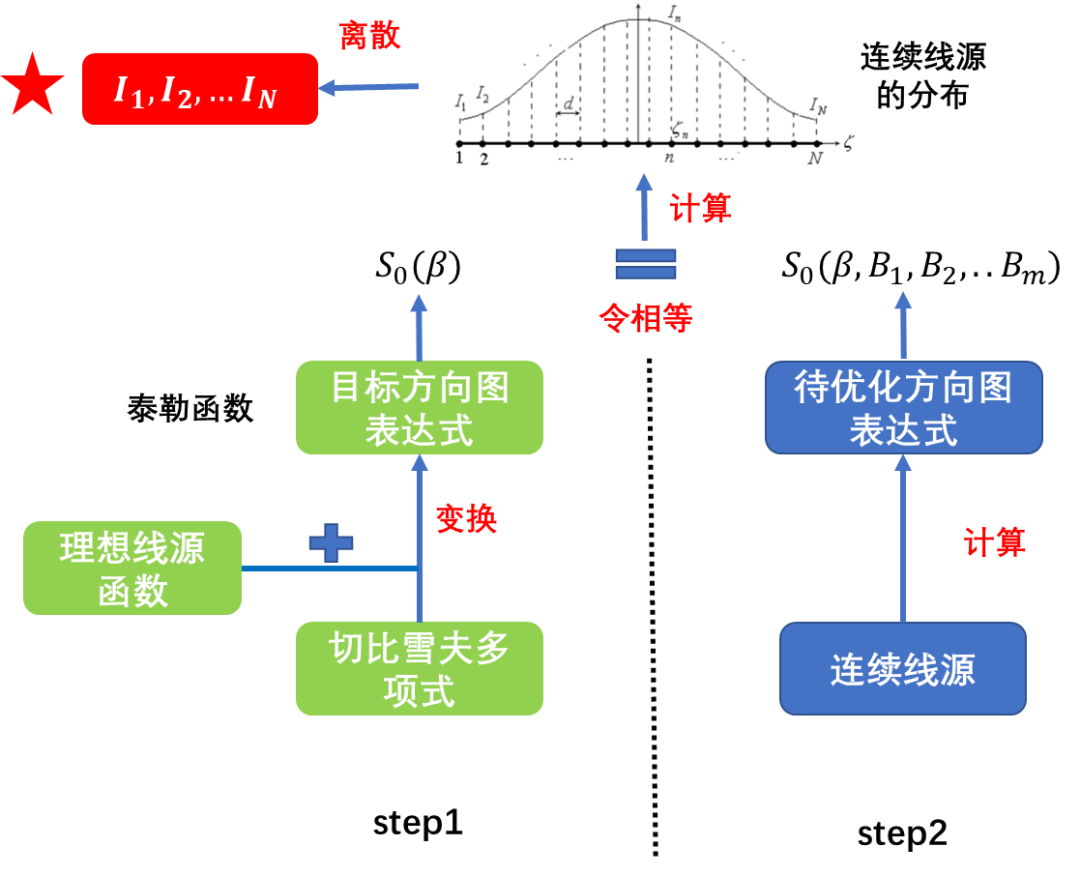
泰勒綜合的參考函數(shù)起源于切比雪夫函數(shù),令,即有:
利用MATLAB繪制其曲線如圖所示,其與陣因子方向圖十分相似:
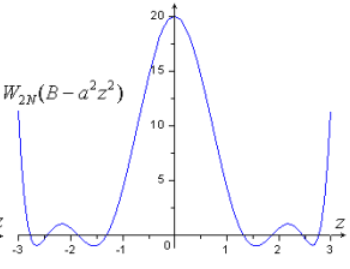
當(dāng)變量N趨于時,參考函數(shù)就轉(zhuǎn)化為理想線源的空間陣因子:
其方向圖形式為:
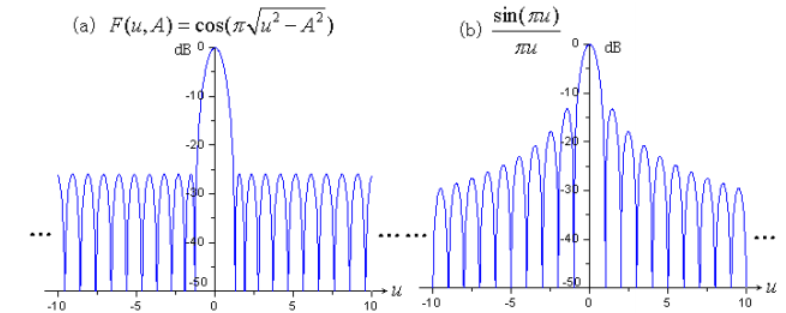
為等副瓣形式,通過引入基本函數(shù)波瓣展寬因子,改造基本函數(shù),構(gòu)建泰勒方向圖函數(shù):
該方向圖函數(shù)的含義是:把基本函數(shù)前個零點(diǎn)用于改造的理想空間因子的零點(diǎn)取代,而第個以后的零點(diǎn)保持為基本函數(shù)的零點(diǎn)。
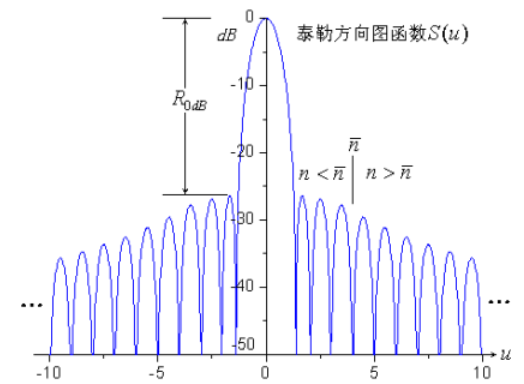
所構(gòu)造的泰勒方向圖函數(shù)既保持了理想空間因子可調(diào)副瓣電平和前個副瓣近似相等的性質(zhì),又在遠(yuǎn)副瓣(第個及以后)保持了基本函數(shù)的副瓣峰值以衰減的性質(zhì)。總結(jié)下來,泰勒函數(shù)的構(gòu)造過程如下圖所示:
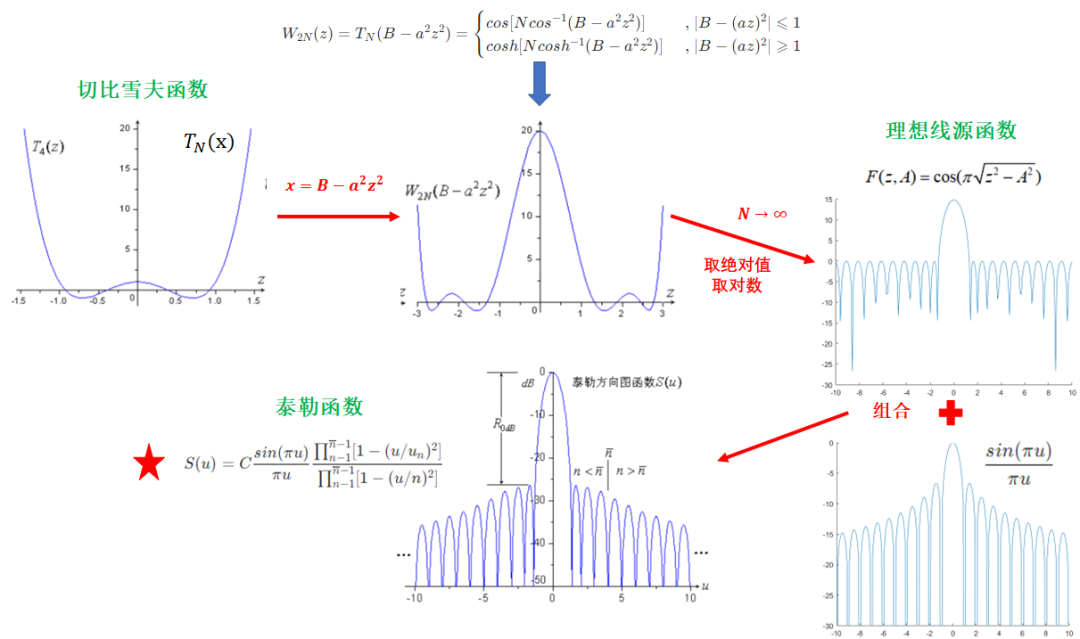
第一步,我們已經(jīng)構(gòu)造了一個完美的方向圖函數(shù),其有著可調(diào)的副瓣電平以及遞減的旁瓣,現(xiàn)在所要做的就是朝著這個完美的方向圖函數(shù)努力前進(jìn),讓待優(yōu)化陣因子與其相等,從而求出陣元幅度分布即可。
連續(xù)線源的方向圖?
從連續(xù)線源的方向圖分布聊起,假設(shè)其電流分布為:
其中展開系數(shù)為未知項,該電流分布所對應(yīng)的空間陣因子的表達(dá)式為:
這就是待優(yōu)化陣因子的表達(dá)式,令其等于泰勒方向圖陣因子,即可求解出展開系數(shù)從而完成了連續(xù)線源電流分布的綜合。
上式即為綜合得到的連續(xù)線源的電流分布。對于直線陣列的各單元的饋電分布,只需要對連續(xù)電流進(jìn)行抽樣離散即可。
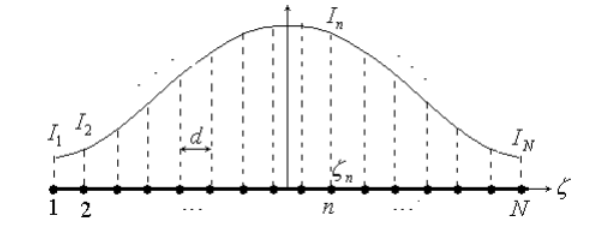
即為每個陣元的饋電幅度,其中,,
實(shí)際設(shè)計過程中,以上的綜合過程無需設(shè)計師手動計算,MATLAB中內(nèi)置Taylor函數(shù),可以按照陣元數(shù)目、主副瓣比SLL和值,直接綜合出相應(yīng)的饋電分布。
N=64;%陣元數(shù)目 n=4;%遠(yuǎn)副瓣位置 SLL=-35;%副瓣電平 w?=?taylorwin(N,n,SLL); %輸出陣元幅度分布 wvtool(w);%查看陣元幅度分布及方向圖預(yù)覽
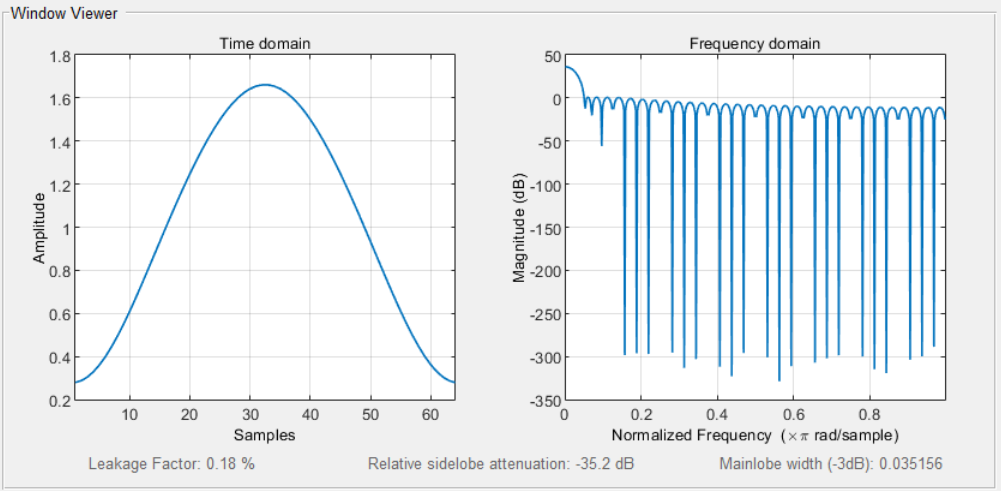
泰勒綜合設(shè)計準(zhǔn)則
依據(jù)主副瓣比選擇合適的,的含義是泰勒方向圖的前個副瓣近似相等,其應(yīng)該根據(jù)主副瓣比來選擇,一般可取,其中,為主副瓣比。
泰勒綜合的單元數(shù)目不能太少,否則按主副瓣電平比的陣列方向圖副瓣電平,不能達(dá)到設(shè)計目的。
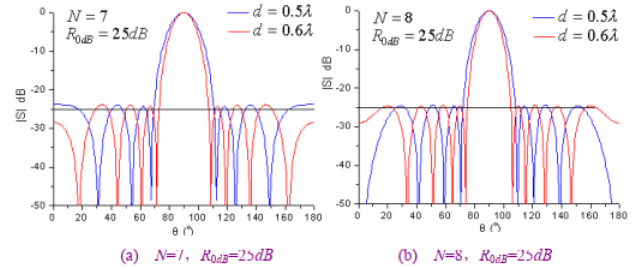
在陣列天線設(shè)計中,各單元的激勵分布都是理想分布。然而實(shí)際加工出來的饋電網(wǎng)絡(luò)總是存在誤差,加之單元間的互耦誤差等,陣列天線的副瓣電平實(shí)測值會有所惡化,因此副瓣電平設(shè)計值需留有余量,一般取7~10dB。
2.平面陣列分析與綜合?
2.1 平面陣列分析?
基于直線陣列的基本原理,依托可分離原理,重點(diǎn)介紹“矩形柵格”形式的平面陣列。
陣因子方向圖
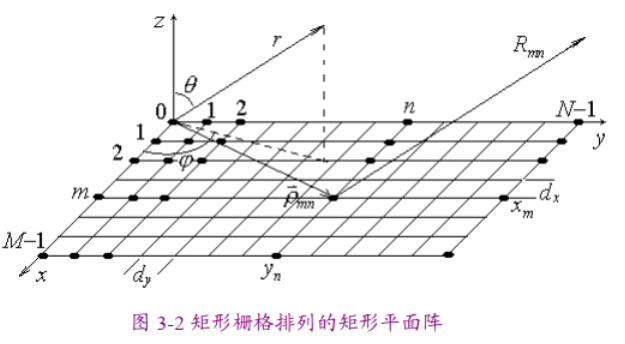
直線陣中方向圖表達(dá)通式也可以被應(yīng)用于平面陣列,任意形式單元天線的遠(yuǎn)區(qū)輻射場可以統(tǒng)一表示為一下形式:
其中表示每個天線單元的饋電(幅度和相位),表示由于天線電流的分布導(dǎo)致遠(yuǎn)場分布的方向性,即單元方向圖,而則是“格林函數(shù)”項,表示理想點(diǎn)源的遠(yuǎn)場分布形式。三部分共同框定了天線單元對遠(yuǎn)場輻射總場的貢獻(xiàn)。
其中:
則第mn個單元的遠(yuǎn)區(qū)輻射場為:
整個平面陣的遠(yuǎn)區(qū)輻射場為:
如果平面陣按列分布為;按行的分布為,則總的饋電幅相為:
為可分離型。可分離型陣列的陣因子也是可分離型的,陣因子為:
其中:
可知,矩形柵格的矩形平面陣列,如果其饋電分布是可分離,則該平面陣列的陣因子方向圖就是沿x和y方向排列的直線陣列陣因子方向圖的乘積,者也是方向圖相乘原理的一種體現(xiàn)。同理,參照均勻直線陣,對于等幅分布的均勻平面陣,其方向圖陣因子可以利用歐拉公式簡化為:
即為均勻直線陣因子的乘積。
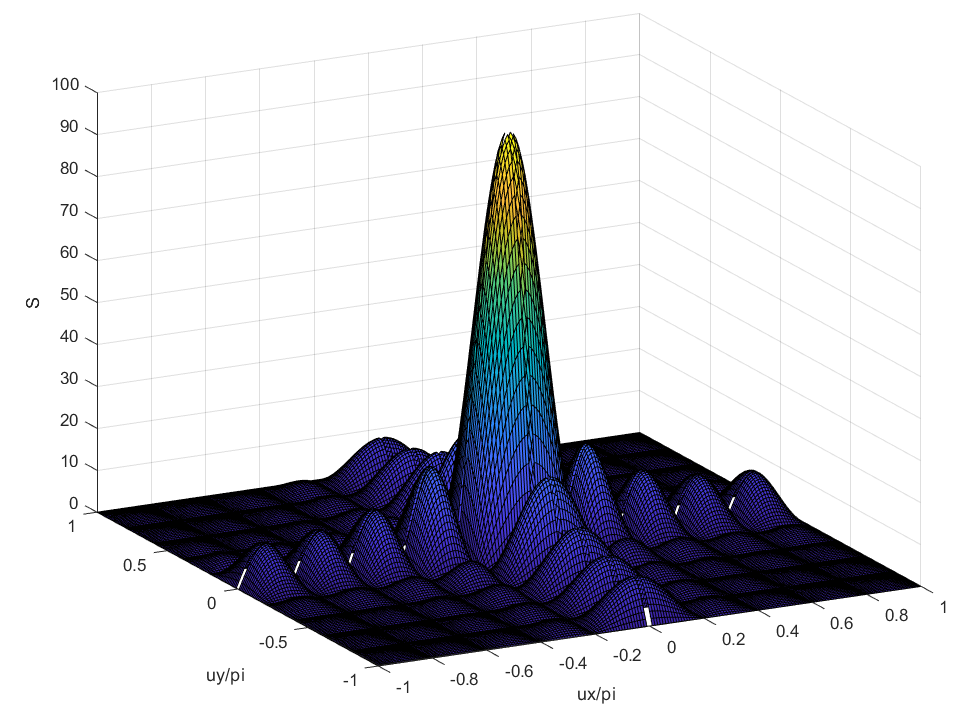
平面波束指向?
波束掃描的核心就是:饋電相位差等于波程差
1)當(dāng)時,出現(xiàn)最大值,此時,為波束指向,得:
同理,當(dāng)時,出現(xiàn)最大值,得:
聯(lián)立可以解的波束指向 ,相反得,可以按照期望波束指向可以求得饋電相位差。
波束寬度?
經(jīng)線所在平面內(nèi)的半功率波瓣寬度
當(dāng)(最大指向在xz平面內(nèi)):
當(dāng)(最大指向在xz平面內(nèi)):
緯線切線所在平面的半功率波瓣寬度
當(dāng)(最大指向在xz平面內(nèi)):
當(dāng)(最大指向在xz平面內(nèi)):
即波束沿俯仰向進(jìn)行掃描時,經(jīng)向所在平面的波瓣寬度會逐漸展寬,而緯線切線所在平面額波瓣寬度不變。
方向性系數(shù)D
方向性系數(shù)的定義為最大增益與平均增益之比,即:
此處假設(shè)陣列數(shù)目非常多,單元方向圖近似單元陣因子。
對于均勻直線陣:
2.2 平面陣列綜合?
切比雪夫綜合法?
矩形柵格矩形邊界的切比雪夫平面陣有兩種形式,一種是可分離型分布的切比雪夫平面陣;另一種是不可分離分布的切比雪夫平面陣。 此處介紹簡單且更為常用的可分離型切比雪夫平面,其設(shè)計較為簡單,即沿兩個主平面方向圖指標(biāo)(主瓣寬度、副瓣電平),分別設(shè)計沿x軸和y軸兩個方向排列的直線陣即可。
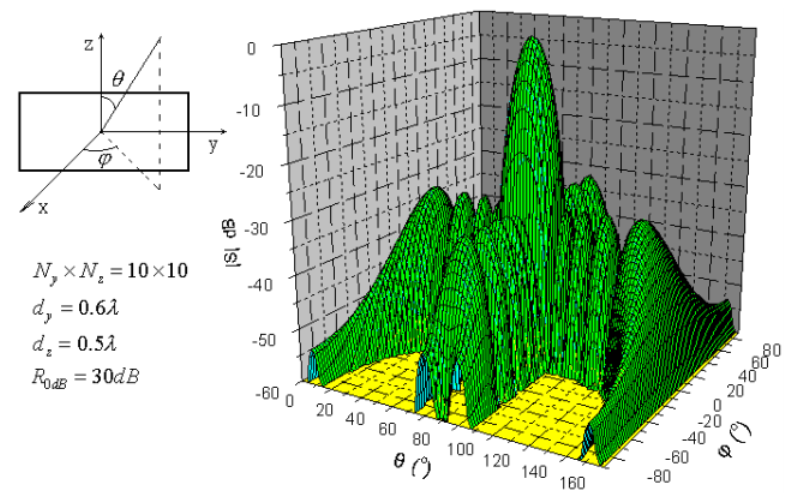
平面各陣元的饋電幅度可以通過直線陣列直接相乘得到。
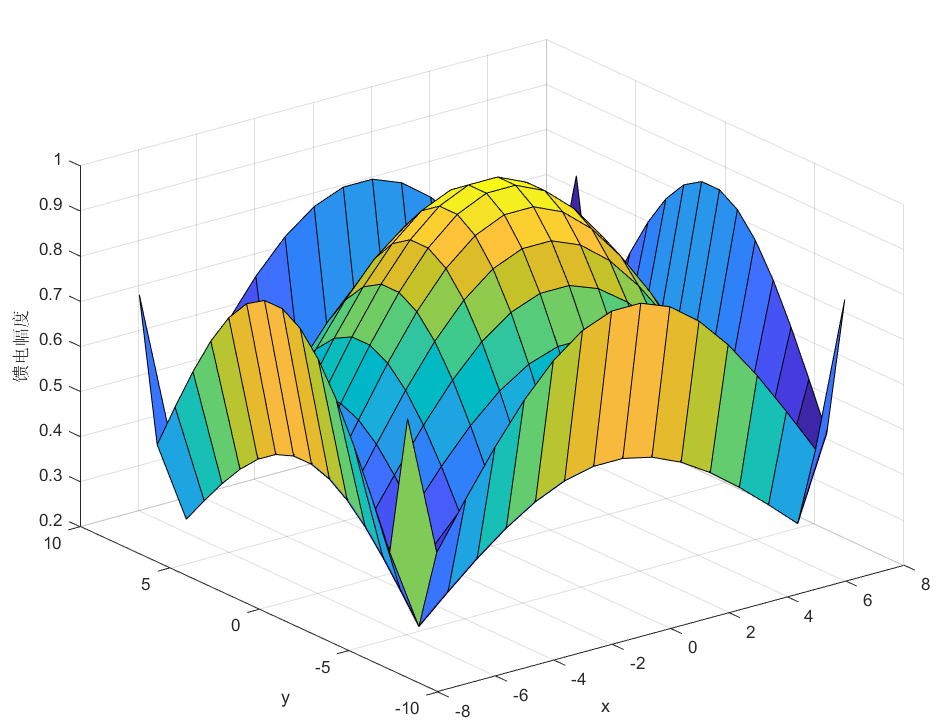
clc;clear?all; [x,y]=meshgrid(-7.57.5,-7.57.5); Nx=16;%x方向陣元數(shù)目 Ny=16;%y方向陣元數(shù)目 SLL=20;%副瓣電平 wx?=?chebwin(Nx,SLL);%輸出x方向陣元幅度分布 wy=chebwin(Nx,SLL);%輸出y方向陣元幅度分布 Wxy=wx.*wy'; %直線陣列的饋電幅度分布相乘得到平面陣 surf(x,y,Wxy); %陣元饋電幅度分布
?
?
泰勒綜合法
陣因子
其中:
類比于泰勒分布的“直線陣列”,圓口徑泰勒分布的“目標(biāo)空間陣因子”為:同樣的,使用連續(xù)面源分布去擬合:計算出待定系數(shù),即可得到圓口徑泰勒面源分布,再經(jīng)過離散就是圓口徑泰勒陣列分布。雖然理論上,圓口徑泰勒分布為不可分離型,但是在實(shí)際工程中,通常也是使用線陣泰勒分布相乘得到面陣的方式來設(shè)計泰勒分布陣列天線。
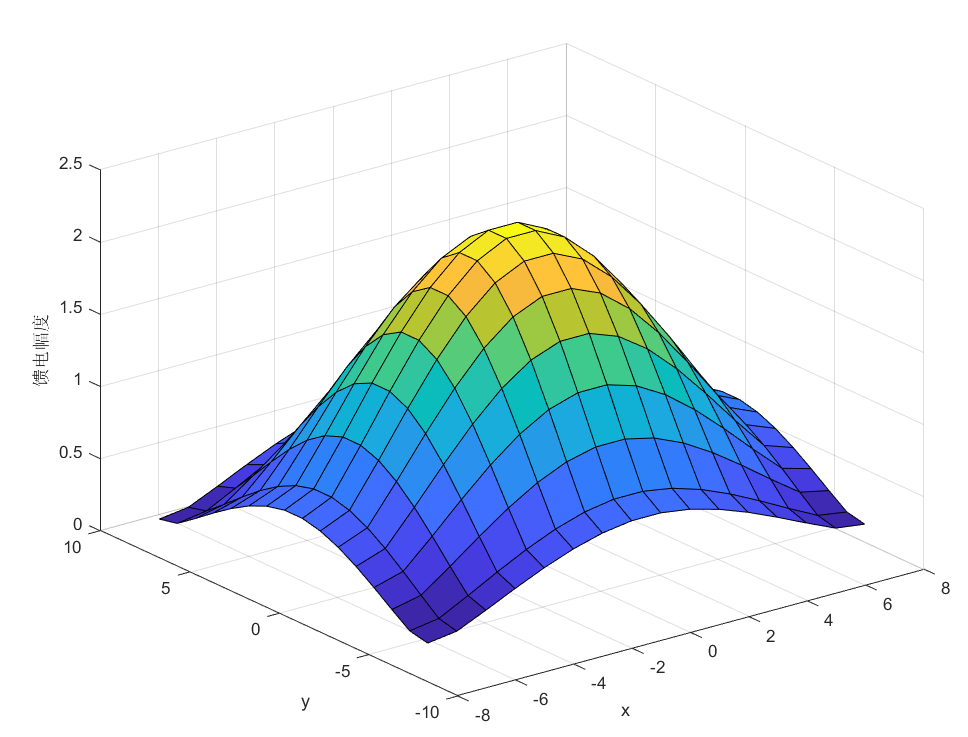
clc;clear?all; [x,y]=meshgrid(-7.57.5,-7.57.5); Nx=16;%x方向陣元數(shù)目 Ny=16;%y方向陣元數(shù)目 SLL=20;%副瓣電平 wx=taylorwin(Nx,SLL);%輸出x方向陣元幅度分布 wy=taylorwin(Nx,SLL);%輸出y方向陣元幅度分布 Wxy=wx.*wy'; surf(x,y,Wxy);
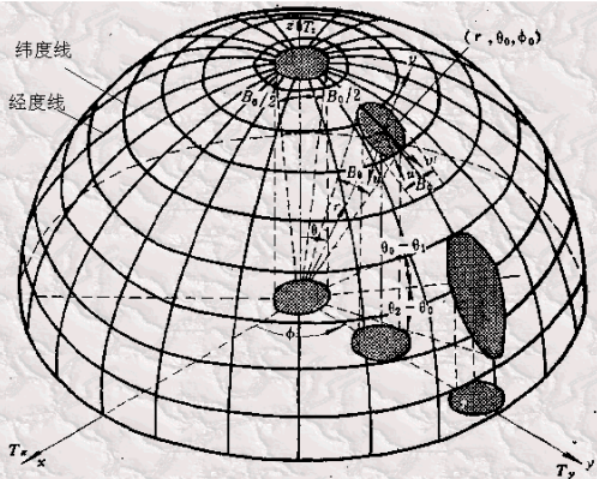
3. 單脈沖體制?
陣列天線的方向圖中的和波束和差波束被廣泛關(guān)注,其背景即為雷達(dá)搜索中的”單脈沖體制“。通過窄波束掃描獲得目標(biāo)的位置和距離信息是現(xiàn)代雷達(dá)的主要功能,其中“單脈沖技術(shù)”為應(yīng)用最普遍的技術(shù)體制。(圖片來自網(wǎng)絡(luò))

單脈沖雷達(dá)天線要求產(chǎn)生一個主瓣的和波束以及具有兩個(或四個)主瓣的差波束。差波束的兩個峰值之間的最小值稱為“零值”。和波束的作用是探測目標(biāo)的距離(r)和進(jìn)行距離跟蹤;差波束的作用是探測目標(biāo)的方位角和俯仰角信息(,)和進(jìn)行角跟蹤。
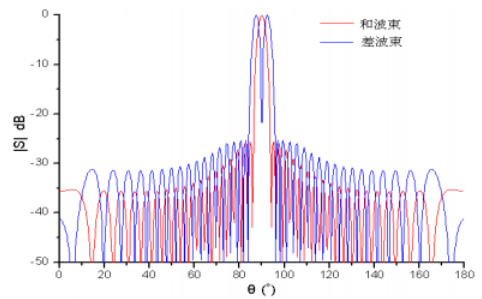
一個目標(biāo)的距離信息 r 和角信息, 已知, 則目標(biāo)的空間位置就確定了。如果目標(biāo)正好在和波束最大值方向, 則差波束接收到的信號很弱(為零值);當(dāng)目標(biāo)移動時, 則差波束接收到的信號由弱變強(qiáng), 則可利用差信號來驅(qū)動伺服機(jī)構(gòu), 使天線在俯仰或方位上轉(zhuǎn)動,始終使差波束的零值方向?qū)?zhǔn)目標(biāo),從而實(shí)現(xiàn)跟蹤 ,同時利用和波束接收到的回波信號時間差確定目標(biāo)距離。
結(jié)語
本文為”陣列天線的分析和綜合基礎(chǔ)“的理論篇,分為直線陣列和平面陣列兩大類進(jìn)行展開,介紹了”分析“和”綜合“兩部分,其中”分析“為依據(jù)陣列天線確定的幅、相分布來計算其輻射特性;”綜合“則根據(jù)總體提供的方向圖要求(主瓣增益、副瓣電平等參數(shù))來反向確定天線的幅、相分布。全文在于解決”陣列天線設(shè)計“的前兩步:1)由淺入深的理解陣列天線的輻射機(jī)理;2)按照陣列天線設(shè)計指標(biāo),完成陣列天線單元數(shù)目、幅相分布的計算。下一篇為”實(shí)踐篇“,將在理論篇確定的陣列結(jié)構(gòu)、幅相分布的基礎(chǔ)上,介紹”陣列天線設(shè)計“的工程實(shí)現(xiàn)以及相關(guān)使用相關(guān)仿真軟件進(jìn)行”陣列天線設(shè)計“的方法。
編輯:黃飛
?
 電子發(fā)燒友App
電子發(fā)燒友App
























評論