同加法運(yùn)算一樣,減法運(yùn)算可采用減法器來實(shí)現(xiàn)。半減器和全減器的設(shè)計(jì)方法和步驟與設(shè)計(jì)加法器相同。實(shí)用上,為了簡化系統(tǒng)結(jié)構(gòu)
,通常不另外設(shè)計(jì)減法器,而是將減法運(yùn)算變?yōu)榧臃ㄟ\(yùn)算來處理,使運(yùn)算器既能實(shí)現(xiàn)加法運(yùn)算,又可實(shí)現(xiàn)減法運(yùn)算。一般采用加補(bǔ)碼的方法代替減法運(yùn)算,下面先來介紹這種方法的原理。
1.反碼和補(bǔ)碼
這里只討論數(shù)值碼,即數(shù)碼中不包括符號位。以前應(yīng)用的自然二進(jìn)制碼稱為原碼,所謂反碼就是將原碼中的所有0變?yōu)?,所有1變?yōu)?后的代碼。觀察如下幾組原碼與反碼之間的關(guān)系。

顯然,每組反碼都是從1111中減去原碼的結(jié)果,所以,可得如下反碼與原碼的一般關(guān)系式:N反=(2n-1)-N原
其中N等于數(shù)碼的位數(shù)。
定義補(bǔ)碼為:N補(bǔ)=2n-N原
于是,便可得到補(bǔ)碼和反碼的關(guān)系式:N補(bǔ)=N反+1
由以上分析可知,一個數(shù)的反碼可將原碼經(jīng)反相器獲得,而由反碼加1就可得到補(bǔ)碼。
2.由加補(bǔ)碼完成減法運(yùn)算
由反碼與原碼的一般關(guān)系式可得兩數(shù)A、B相減的表達(dá)式:

上式表明A減B可由A加B的補(bǔ)碼并減2n完成。
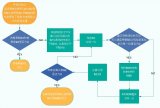
下圖為4位減法運(yùn)算電路圖:

由4個反相器將B的各位反相(求反),并將進(jìn)位輸入端C-1接邏輯1以實(shí)現(xiàn)加1,由此求得B的補(bǔ)碼。顯然,只能由高位的進(jìn)位信號與2n相減。當(dāng)最高位的進(jìn)位信號為1(2n)時(shí),它們的差為0;最高位的進(jìn)位信號為0時(shí),它與2n相減所得的差為1,同時(shí)還應(yīng)發(fā)出借位信號。因此,只要將最高位的進(jìn)位信號反相即實(shí)現(xiàn)了減2n的運(yùn)算,反相器的輸出V為1時(shí)需要借位,故V為借位信號。下面分兩種情況分析減法運(yùn)算過程。
(1)A-B≥0的情況。
設(shè)A=0101,B=0001。
求補(bǔ)相加演算過程如下:

直接作減法演算,則有 
比較兩種運(yùn)算結(jié)果,它們完全相同。在A-B≥0時(shí),所得的差就是差的原碼,借位信號為0。
(2)A-B<0的情況。
設(shè)A=0001,B=0101。
求補(bǔ)相加演算過程如下:

直接作減法運(yùn)算,則有:
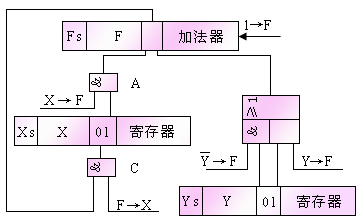
比較兩種運(yùn)算結(jié)果可知,前者正好是后者的絕對值的補(bǔ)碼,借位信號V為1時(shí)表示差為負(fù)數(shù),V為0時(shí)差為正數(shù)。若要求差值以原碼形式輸出,則還需進(jìn)行變換。由補(bǔ)碼的定義式可知 ,即將補(bǔ)碼再求補(bǔ)得原碼。這時(shí)的求補(bǔ)邏輯電路如下圖所示:
,即將補(bǔ)碼再求補(bǔ)得原碼。這時(shí)的求補(bǔ)邏輯電路如下圖所示:

結(jié)合4位減法運(yùn)算邏輯電路和這個求補(bǔ)邏輯電路可組成輸出為原碼的完整的4位減法運(yùn)算電路。求補(bǔ)相加而得的差輸入到不同的異或門的一個輸入端,而另一輸入端由借位信號V控制。當(dāng)V=1時(shí),D3~D0反相,加法器也不實(shí)現(xiàn)加1運(yùn)算,維持原碼。
 電子發(fā)燒友App
電子發(fā)燒友App


































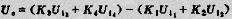











評論