硅是常見的元素，那么地球上有多少硅原子可以用來生成晶體管

硅是一種極為常見的元素，廣泛存在于巖石、砂礫、塵土之中。在地殼中，硅是含量第二豐富的元素，構成地殼總質量的26.4%，僅次于第一位的氧(49.4%)。

坐在沙灘上，望著浩瀚無邊的大海，雙手捧起一捧沙子，讓沙粒從指間慢慢滑落，我們可能會想，沙子，應該是取之不盡、用之不竭的吧！

第** 1 **個問題

地球上有多少個硅原子？

地球總質量：5.965×10^24 kg

地殼占地球總質量的：0.42%

硅元素占地殼總質量的：26.4%

地球上硅元素總質量：

5.965×10^24×0.42%×26.4%=6.614×10^21kg

約為地球總質量的千分之一

硅原子質量為：28×1.674×10^-27kg（氫原子質量）=4.687×10^-26kg

地球上硅原子總數(shù)：

6.614×10^21/4.687×10^-26=1.41×10^47個

**1.41×10^47 **個

第** 2 **個問題

一個晶體管需要多少個硅原子？

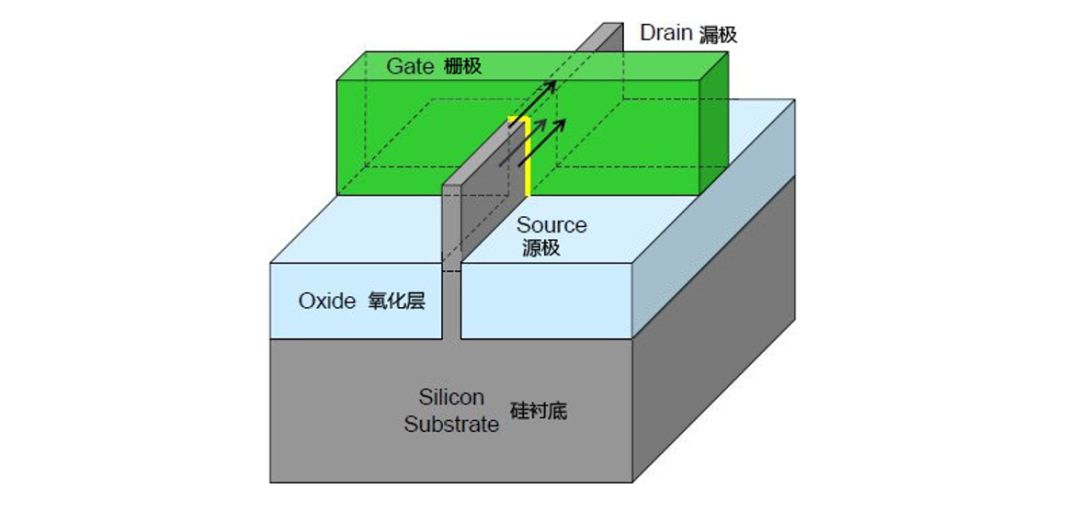
要回答這個問題，首先我們得知道晶體管的體積，人們經常說的10nm、7nm、5nm、3nm是指的晶體管的特征尺寸。特征尺寸是晶體管中的最小尺寸，以CMOS工藝為例，特征尺寸典型代表為柵的寬度，也即MOS器件的溝道長度。一般來說，特征尺寸越小，芯片的集成度越高，性能越好，功耗越低。

而晶體管的體積（邊長）自然要比特征尺寸大得多，應該是多少呢？

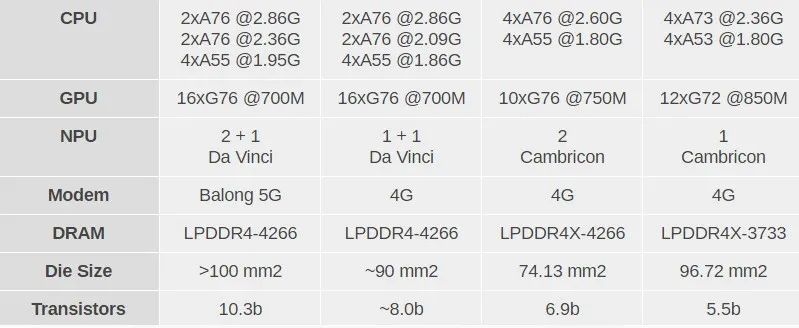
上圖為某芯片的數(shù)據圖，每平方毫米集成約1億（10^8）只晶體管。

1平方毫米=10^12平方納米

10^12平方納米/10^8個=10^4平方納米

由此可知，每一只晶體管的面積約為10000平方納米

假定晶體管為正方形，則邊長為100nm

假定晶體管的高也約為100nm，則一個晶體管體積為10^6立方納米

1立方納米硅由多少硅原子組成？答案：50個

計算方法如下：

硅的密度：2328.3 kg/m3

硅原子質量：28×1.674×10^-27kg

1立方納米包含的硅原子

=2328.3÷28÷1.674=49.7≈ 50

1個晶體管組成的硅原子數(shù)

=50×100×100×100=5000萬個硅原子

是不是這樣就可以算出地球上的硅總共能生產多少個晶體管？

請稍等，我們看下面一張圖

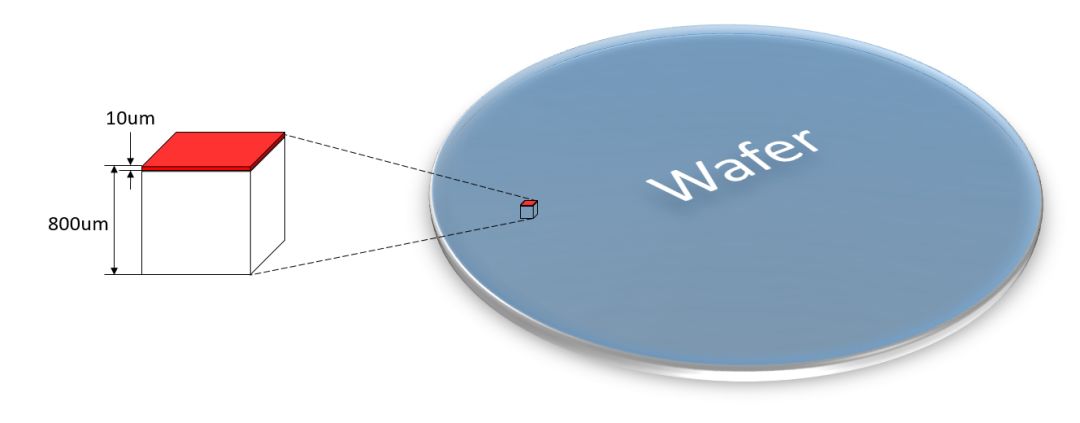
雖然晶體管本身的厚度約為100nm，芯片有源區(qū)的厚度不到10um，但其下方支撐的硅體卻大約有1mm，如何得出？首先，晶元厚度一般為800um，晶元切割損耗約為200um，800+200=1000um=1mm。

1個晶體管占有（消耗）的硅原子數(shù)為50×100(長)×100(寬)×10^6(厚度)

=5×10^11=5000億個硅原子，這就是說，晶體管本身所占的硅原子只占晶元中硅原子的萬分之一，99.99%的硅原子只是作為陪襯，在生產過程中被占用或者被消耗掉了。

以臺積電7nm工藝生產一只晶體管消耗的硅原子不是5000萬個而是5000億個！

1個Transistor=****5000億 ****個硅原子

第3個問題

地球上的硅能生產多少只晶體管？

以現(xiàn)有的采用臺積電7nm FinFET Plus EUV工藝制造的晶體管，地球上的硅可生產的晶體管數(shù)量為：地球上的硅原子數(shù)量÷每一晶體管所消耗的晶體管數(shù)量，如下

1.41×10^47÷(5×10^11)= 2.82×10^35個

地球上的硅可生產的晶體管數(shù)量為：

**2.82×10^35 **個晶體管

得到這個答案后，問題就到此為止了嗎？

沒有，這僅僅只是個開始！

第4個問題

地球上的硅能用多久？

上面提到某款處理器含有約103億晶體管，其面積約為100平方mm。

實際上硅的消耗量和并非和晶體管數(shù)量相關，而是和芯片的面積相關，因為工藝不同，晶體管大小不同，消耗的硅原子數(shù)量也不同，而芯片的面積(體積)卻和硅原子數(shù)量直接相關。

回答第二個問題時，上面我們已經推導出1立方nm的硅中包含的原子數(shù)量為：50 個，那么，1立方mm的硅中包含的原子數(shù)量為：50×10^18個，等同于1平方mm晶元中所包含的硅原子。一個100平方mm的芯片，一顆芯片消耗的硅原子數(shù)量為：100×50×10^18個，即5×10^21個硅原子。

以這樣的芯片為例，地球上的硅總共可以生產的芯片的數(shù)量為：1.41×10^47 ÷ (5×10^21) = 2.82×10^25個。

2019年，中國總共生產了2018.2億塊芯片，約占全球芯片產量的10%，可以估算全球芯片產量超過20182億塊，約為2×10^12塊。

芯片的面積有大有小，我們暫且以100平方mm為其中位數(shù)，則每年需要消耗的硅原子數(shù)量為：（2×10^12）×（5×10^21）=10^34個，假定芯片年產量不變，則地球上的硅可用時間為：1.41×10^47÷10^34=1.41×10^13 年，也就是14.1萬億年。看來，我們還不用擔心，地球的壽命也不見得有那么長。

但是，事實卻是：每一年，芯片的需求和產量都會有所增加。

2019年全球芯片產值4376億美元，產量約為2×10^12（20182億）塊。

這里，我們做一個假設，假設全球芯片產值不變，但芯片價格越來越便宜，用同樣的美元可買到的芯片數(shù)量，每隔9-12個月翻一番。

2×10^12 × (1+2+2^2+2^3+...+2^n) = 2.82×10^25，求解得到的n則為可生產的年數(shù)。

(1+2+2^2+2^3+...+2^n) = 1.41×10^13

[2^(n+1)-1]=1.41×10^13

2^n=7.05×10^12

n=42.68<43

也就是說，如果同樣的美元可買到的芯片數(shù)量每隔9-12個月翻一番，不到 43 年，地球上的硅原子就要用完了。

這不太可能吧，一定是我們的假設有問題，這時候，耳邊飄來一句話：“用一個美元所能買到的電腦性能，每隔18-24個月翻兩番”。

每隔18-24個月翻兩番和每隔9-12個月翻一番應該是相同的意思，不過電腦的性能并不等同芯片的數(shù)量，但其中還是有一定的相關性的。

我們知道：“用一個美元所能買到的電腦性能，每隔18-24個月翻兩番”正是摩爾定律的內容。

地球上的硅到底夠用14萬億年還是43年呢？

兩者各有什么問題，聰明的讀者，你知道嗎？

第5個問題

摩爾定律還能再持續(xù)嗎？

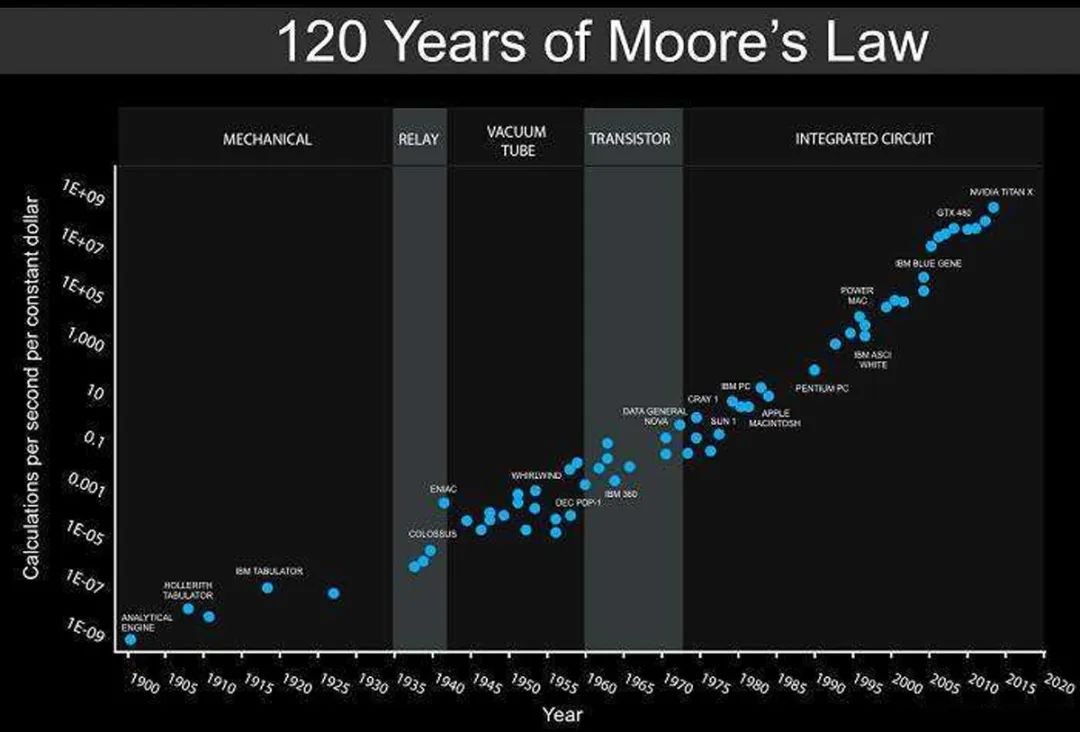
摩爾定律內容為：當價格不變時，集成電路上可容納的元器件的數(shù)目，約每隔18-24個月便會增加一倍，性能也將提升一倍。換言之，每一美元所能買到的電腦性能，將每隔18-24個月翻一倍以上（翻兩番）。

摩爾定律里的”元器件的數(shù)目“實際就是晶體管Transistor數(shù)目。

我們就以某款 5G處理器為例，內含晶體管數(shù)量約為100億，2019芯片產量約為20000億只。當然，很多芯片內的數(shù)量達不到這么多，但也有芯片中晶體管數(shù)量遠遠超過百億，例如WSE芯片中晶體管數(shù)量達到了1.2 萬億。目前以7nm主流工藝生產的芯片，其晶體管數(shù)量差不多都在百億量級了。

20000×10^8×100×10^8×(1+2+2^2+2^3+...+2^n) =2.82×10^35

2×10^22 (1+2+2^2+2^3+...+2^n) =2.82×10^35

(1+2+2^2+2^3+...+2^n) = 1.41×10^13

[2^(n+1)-1]=1.41×10^13

2^n=7.05×10^12

n=42.68<43

如果是每隔18個月翻一番，則43×1.5=64.5<65年，如果是每隔24個月翻一番，則43×2= 86 年

也就是說，只要 65 年或者最多 86 年，地球上的硅原子就要用完了！

而且，我們估算時只考慮了硅在芯片制造上的應用，即硅僅僅用來制作高純硅半導體。

實際上是，除此之外，硅還廣泛應用于耐高溫材料、光導纖維通信材料、有機硅化合物、合金等，硅被廣泛應用于航空航天、電子電氣、運輸、能源、化工、紡織、食品、輕工、醫(yī)療、農業(yè)等行業(yè)。

另外，我們還沒有考慮其它的應用，例如修路、修橋、修房子... 這些大量應用石頭和沙子等硅化合物的領域。








審核編輯：劉清