?

神經(jīng)網(wǎng)絡(luò)模型的每一類學(xué)習(xí)過程通常被歸納為一種訓(xùn)練算法。訓(xùn)練的算法有很多，它們的特點(diǎn)和性能各不相同。

?

問題的抽象
人們把神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)過程轉(zhuǎn)化為求損失函數(shù)f的最小值問題。一般來說，損失函數(shù)包括誤差項和正則項兩部分。誤差項衡量神經(jīng)網(wǎng)絡(luò)模型在訓(xùn)練數(shù)據(jù)集上的擬合程度，而正則項則是控制模型的復(fù)雜程度，防止出現(xiàn)過擬合現(xiàn)象。

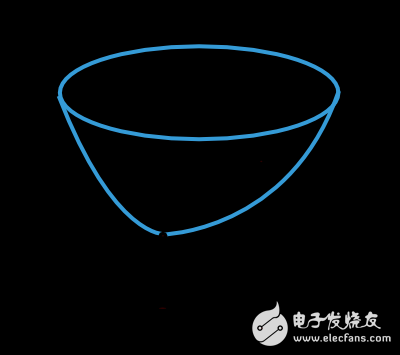
損失函數(shù)的函數(shù)值由模型的參數(shù)（權(quán)重值和偏置值）所決定。我們可以把兩部分參數(shù)合并為一個n維的權(quán)重向量，記為w。下圖是損失函數(shù)f(w)的圖示。

?

如上圖所示，w*是損失函數(shù)的最小值。在空間內(nèi)任意選擇一個點(diǎn)A，我們都能計算得到損失函數(shù)的一階、二階導(dǎo)數(shù)。一階導(dǎo)數(shù)可以表示為一個向量：

?if(w) = df/dwi (i = 1,…,n)

同樣的，損失函數(shù)的二階導(dǎo)數(shù)可以表示為海森矩陣（ Hessian Matrix ）：

Hi,jf(w) = d2f/dwi·dwj (i,j = 1,…,n)

多變量的連續(xù)可微分函數(shù)的求解問題一直被人們廣泛地研究。許多的傳統(tǒng)方法都能被直接用于神經(jīng)網(wǎng)絡(luò)模型的求解。

一維優(yōu)化方法
盡管損失函數(shù)的值需要由多個參數(shù)決定，但是一維優(yōu)化方法在這里也非常重要。這些方法常常用于訓(xùn)練神經(jīng)網(wǎng)絡(luò)模型。

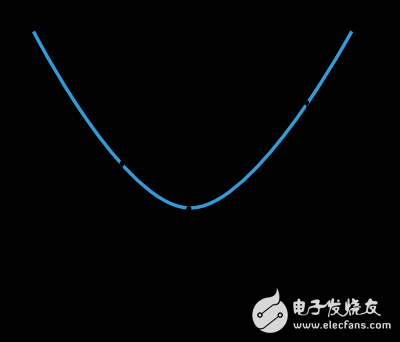
許多訓(xùn)練算法首先計算得到一個訓(xùn)練的方向d，以及速率η來表示損失值在此方向上的變化，f(η)。下圖片展示了這種一維函數(shù)。

?

f和η*在η1和η2所在的區(qū)間之內(nèi)。

由此可見，一維優(yōu)化方法就是尋找到某個給定的一維函數(shù)的最小值。黃金分段法和Brent方法就是其中兩種廣泛應(yīng)用的算法。這兩種算法不斷地縮減最小值的范圍，直到η1和η2兩點(diǎn)之間的距離小于設(shè)定的閾值。

多維優(yōu)化方法
我們把神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)問題抽象為尋找參數(shù)向量w*的問題，使得損失函數(shù)f在此點(diǎn)取到最小值。假設(shè)我們找到了損失函數(shù)的最小值點(diǎn)，那么就認(rèn)為神經(jīng)網(wǎng)絡(luò)函數(shù)在此處的梯度等于零。

通常情況下，損失函數(shù)屬于非線性函數(shù)，我們很難用訓(xùn)練算法準(zhǔn)確地求得最優(yōu)解。因此，我們嘗試在參數(shù)空間內(nèi)逐步搜索，來尋找最優(yōu)解。每搜索一步，重新計算神經(jīng)網(wǎng)絡(luò)模型的參數(shù)，損失值則相應(yīng)地減小。

我們先隨機(jī)初始化一組模型參數(shù)。接著，每次迭代更新這組參數(shù)，損失函數(shù)值也隨之減小。當(dāng)某個特定條件或是終止條件得到滿足時，整個訓(xùn)練過程即結(jié)束。

現(xiàn)在我們就來介紹幾種神經(jīng)網(wǎng)絡(luò)的最重要訓(xùn)練算法。

?

1. 梯度下降法（Gradient descent）

梯度下降方法是最簡單的訓(xùn)練算法。它僅需要用到梯度向量的信息，因此屬于一階算法。

我們定義f(wi) = fiand ?f(wi) = gi。算法起始于W0點(diǎn)，然后在第i步沿著di= -gi方向從wi移到wi+1，反復(fù)迭代直到滿足終止條件。梯度下降算法的迭代公式為：

wi+1 = wi- di·ηi, i=0,1,…

參數(shù)η是學(xué)習(xí)率。這個參數(shù)既可以設(shè)置為固定值，也可以用一維優(yōu)化方法沿著訓(xùn)練的方向逐步更新計算。人們一般傾向于逐步更新計算學(xué)習(xí)率，但很多軟件和工具仍舊使用固定的學(xué)習(xí)率。

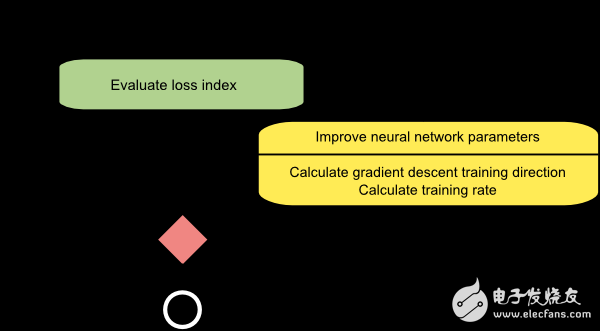
下圖是梯度下降訓(xùn)練方法的流程圖。如圖所示，參數(shù)的更新分為兩步：第一步計算梯度下降的方向，第二步計算合適的學(xué)習(xí)率。

?

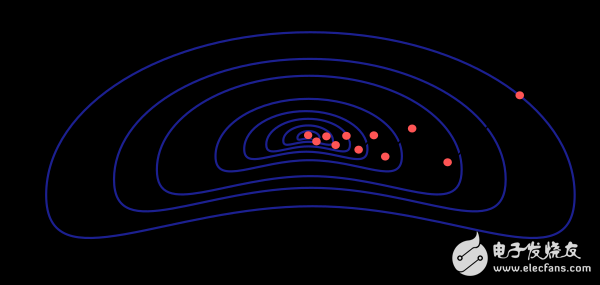
梯度下降方法有一個嚴(yán)重的弊端，若函數(shù)的梯度變化如圖所示呈現(xiàn)出細(xì)長的結(jié)構(gòu)時，該方法需要進(jìn)行很多次迭代運(yùn)算。而且，盡管梯度下降的方向就是損失函數(shù)值減小最快的方向，但是這并不一定是收斂最快的路徑。下圖描述了此問題。

?

當(dāng)神經(jīng)網(wǎng)絡(luò)模型非常龐大、包含上千個參數(shù)時，梯度下降方法是我們推薦的算法。因?yàn)榇朔椒▋H需要存儲梯度向量（n空間），而不需要存儲海森矩陣（n2空間）

2.牛頓算法（Newton’s method）

因?yàn)榕ｎD算法用到了海森矩陣，所以它屬于二階算法。此算法的目標(biāo)是使用損失函數(shù)的二階偏導(dǎo)數(shù)尋找更好的學(xué)習(xí)方向。

?

?

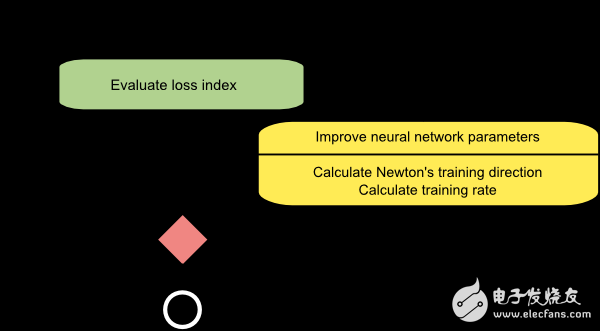
下圖展示的是牛頓法的流程圖。參數(shù)的更新也分為兩步，計算牛頓訓(xùn)練方向和合適的學(xué)習(xí)率。

?

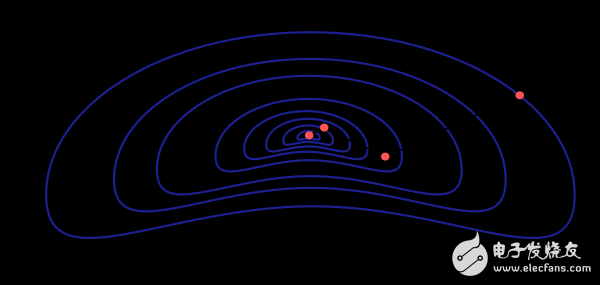
牛頓法的性能如下圖所示。從相同的初始值開始尋找損失函數(shù)的最小值，它比梯度下降方法需要更少的步驟。

?

然而，牛頓法的難點(diǎn)在于準(zhǔn)確計算海森矩陣和其逆矩陣需要大量的計算資源。

3.共軛梯度法（Conjugate gradient）

共軛梯度法介于梯度下降法與牛頓法之間。它的初衷是解決傳統(tǒng)梯度下降法收斂速度太慢的問題。不像牛頓法，共軛梯度法也避免了計算和存儲海森矩陣。

共軛梯度法的搜索是沿著共軛方向進(jìn)行的，通常會比沿著梯度下降法的方向收斂更快。這些訓(xùn)練方向與海森矩陣共軛。

我們將d定義為訓(xùn)練方向向量。然后，將參數(shù)向量和訓(xùn)練方向訓(xùn)練分別初始化為w0和d0 = -g0，共軛梯度法的方向更新公式為：
di+1 = gi+1 + di·γi, i=0,1,…

其中γ是共軛參數(shù)，計算它的方法有許多種。其中兩種常用的方法分別是Fletcher 和 Reeves 以及 *** 和 Ribiere發(fā)明的。對于所有的共軛梯度算法，訓(xùn)練方向會被周期性地重置為梯度的負(fù)值。

參數(shù)的更新方程為：

wi+1 = wi + di·ηi, i=0,1,…

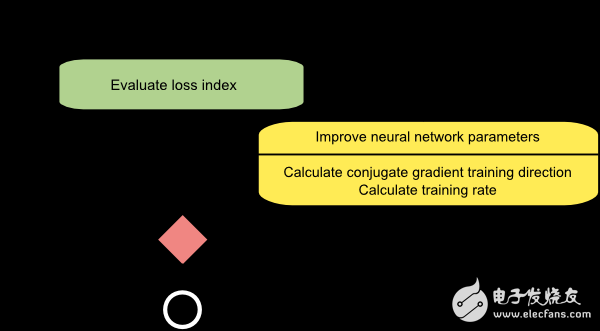
下圖是共軛梯度法訓(xùn)練過程的流程圖。參數(shù)更新的步驟分為計算共軛梯度方向和計算學(xué)習(xí)率兩步。

?

此方法訓(xùn)練神經(jīng)網(wǎng)絡(luò)模型的效率被證明比梯度下降法更好。由于共軛梯度法不需要計算海森矩陣，當(dāng)神經(jīng)網(wǎng)絡(luò)模型較大時我們也建議使用。

4. 準(zhǔn)牛頓法（Quasi-Newton method）

由于牛頓法需要計算海森矩陣和逆矩陣，需要較多的計算資源，因此出現(xiàn)了一個變種算法，稱為準(zhǔn)牛頓法，可以彌補(bǔ)計算量大的缺陷。此方法不是直接計算海森矩陣及其逆矩陣，而是在每一次迭代估計計算海森矩陣的逆矩陣，只需要用到損失函數(shù)的一階偏導(dǎo)數(shù)。

海森矩陣是由損失函數(shù)的二階偏導(dǎo)數(shù)組成。準(zhǔn)牛頓法的主要思想是用另一個矩陣G來估計海森矩陣的逆矩陣，只需要損失函數(shù)的一階偏導(dǎo)數(shù)。準(zhǔn)牛頓法的更新方程可以寫為：
wi+1 = wi - (Gi·gi)·ηi, i=0,1,…

學(xué)習(xí)率η既可以設(shè)為固定值，也可以動態(tài)調(diào)整。海森矩陣逆矩陣的估計G有多種不同類型。兩種常用的類型是Davidon–Fletcher–Powell formula (DFP)和Broyden–Fletcher–Goldfarb–Shanno formula (BFGS)。

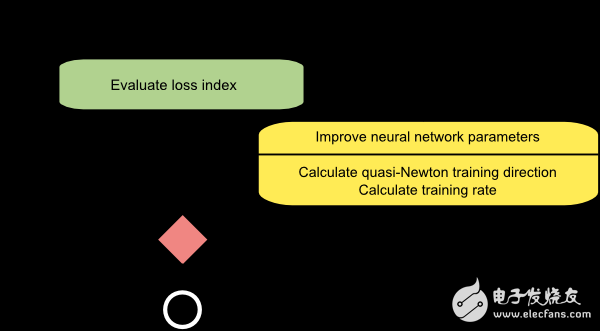
準(zhǔn)牛頓法的流程圖如下所示。參數(shù)更新的步驟分為計算準(zhǔn)牛頓訓(xùn)練方向和計算學(xué)習(xí)率。

?

許多情況下，這是默認(rèn)選擇的算法：它比梯度下降法和共軛梯度法更快，而不需要準(zhǔn)確計算海森矩陣及其逆矩陣。

5. Levenberg-Marquardt算法

Levenberg-Marquardt算法又稱為衰減的最小平方法，它針對損失函數(shù)是平方和誤差的形式。它也不需要準(zhǔn)確計算海森矩陣，需要用到梯度向量和雅各布矩陣。

假設(shè)損失函數(shù)f是平方和誤差的形式：

?

?

若衰減因子λ設(shè)為0，相當(dāng)于是牛頓法。若λ設(shè)置的非常大，這就相當(dāng)于是學(xué)習(xí)率很小的梯度下降法。

參數(shù)λ的初始值非常大，因此前幾步更新是沿著梯度下降方向的。如果某一步迭代更新失敗，則λ擴(kuò)大一些。否則，λ隨著損失值的減小而減小，Levenberg-Marquardt接近牛頓法。這個過程可以加快收斂的速度。

下圖是Levenberg-Marquardt算法訓(xùn)練過程的流程圖。第一步計算損失值、梯度和近似海森矩陣。然后衰減參數(shù)和衰減系數(shù)。

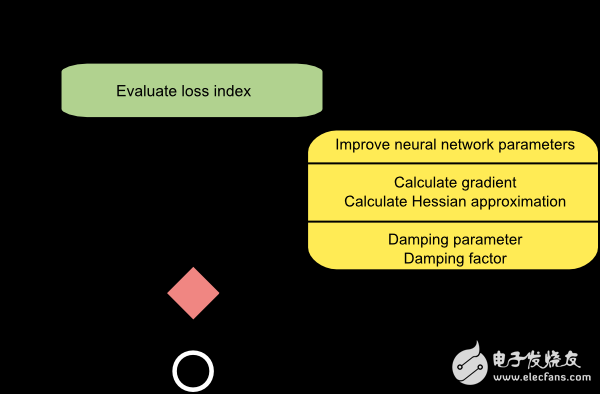
由于Levenberg-Marquardt算法主要針對平方和誤差類的損失函數(shù)。因此，在訓(xùn)練這類誤差的神經(jīng)網(wǎng)絡(luò)模型時速度非常快。但是這個算法也有一些缺點(diǎn)。首先，它不適用于其它類型的損失函數(shù)。而且，它也不兼容正則項。最后，如果訓(xùn)練數(shù)據(jù)和網(wǎng)絡(luò)模型非常大，雅各布矩陣也會變得很大，需要很多內(nèi)存。因此，當(dāng)訓(xùn)練數(shù)據(jù)或是模型很大時，我們并不建議使用Levenberg-Marquardt算法。

內(nèi)存使用和速度的比較
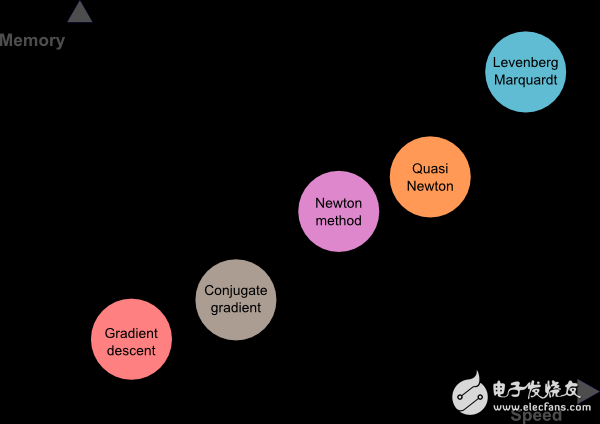
下圖繪制了本文討論的五種算法的計算速度和內(nèi)存需求。如圖所示，梯度下降法往往是最慢的訓(xùn)練方法，它所需要的內(nèi)存也往往最少。相反，速度最快的算法一般是Levenberg-Marquardt，但需要的內(nèi)存也更多。柯西-牛頓法較好地平衡了兩者。

?

總之，如果我們的神經(jīng)網(wǎng)絡(luò)模型有上千個參數(shù)，則可以用節(jié)省存儲的梯度下降法和共軛梯度法。如果我們需要訓(xùn)練很多網(wǎng)絡(luò)模型，每個模型只有幾千個訓(xùn)練數(shù)據(jù)和幾百個參數(shù)，則Levenberg-Marquardt可能會是一個好選擇。其余情況下，柯西-牛頓法的效果都不錯。