計數是一種最簡單基本的運算,計數器就是實現這種運算的邏輯電路,計數器在數字系統中主要是對脈沖的個數進行計數,以實現測量、計數和控制的功能,同時兼有分頻功能,計數器是由基本的計數單元和一些控制門所組成,計數單元則由一系列具有存儲信息功能的各類觸發器構成,這些觸發器有RS觸發器、T觸發器、D觸發器及JK觸發器等。本文為大家帶來七種任意進制計數器設計方案及其電路設計的原理詳解。
任意進制計數器設計方案一:采用反饋置數法來設計任意進制計數器
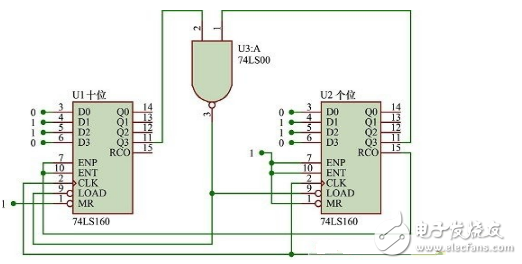
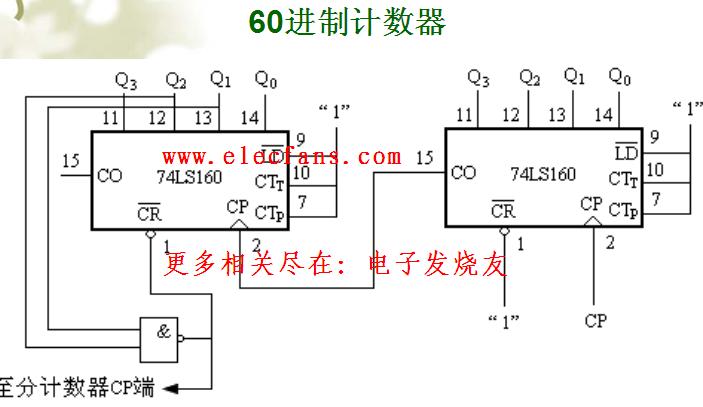
此方法適用于某些具有預置數的計數器,它是采用預置數控制端LOAD來實現。對于74LS160屬于同步式預置數的計數器來說,當LOAD出現有效電平低電平后待下一個時鐘脈沖信號到來后計數器輸出端的狀態Q3Q2Q1Q0=D3D2D1D0.使其跳過某些狀態來設計任意進制計數器。下面就以74LS160為例,用并行置數法設計23進制計數器,其中預置數端D3D2D1D0可以置零,也可以置十以內的任意四位二進制數。那么此電路在其置數時十位和個位的D3D2D1D0置入(01100110)8421BCD碼=(66)10,而反饋代碼十位和個位為(10001000)8421BCD碼=(88)10,相當于十進制數的88.由此分析可得到計數器的模為(88-66)+1=23,故計數器為23進制計數器,其設計電路圖如圖5所示。由此可以得到置數法的設計要點為:反饋代碼轉換成的十進制數-預置數端的代碼轉換成的十進制數+1=所設計的計數器的模。
任意N進制計數器的設計方法及步驟
(1)根據計數模N來確定所需要計數器芯片的個數n.n=INT(logm(N-1))+1,INT表示取整。m:當芯片為十進制計數器時m取10,當芯片為四位二進制計數器時m取16.
(2)當n個計數器芯片連接成模為m的計數器
(3)選用并行法或串行法將n個計數器連接起來。
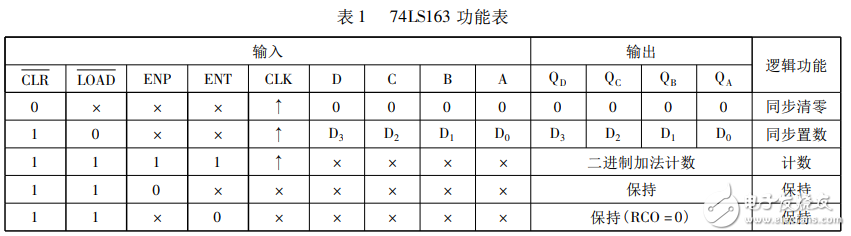
(4)確定反饋置零代碼。如果計數器芯片采用異步置零反饋代碼為(N)10,若是采用同步置零,則反饋代碼為(N??1)10.
(5)反饋置零代碼形式的轉換。如果芯片為十進制制計數器,將反饋代碼轉換成8421BCD碼的形式。若是四位二進制計數器,則將反饋代碼轉換成二進制數。
(6)將轉換結果與計數器的狀態輸出端進行比較,讓與1對應的引腳作用到與非門(反饋置零端低電平有效)或者與門(反饋置零端高電平有效)的輸入端,然后將與非門或者與門的輸出,連接到計數器芯片的反饋置零端即可。
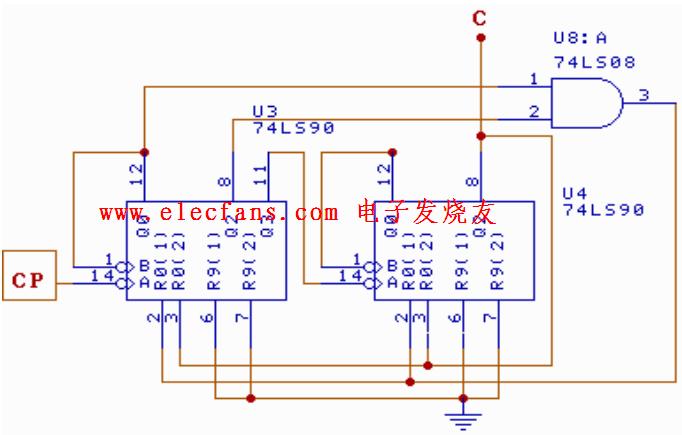
任意進制計數器設計方案二:采用清零法來設計任意進制計數器
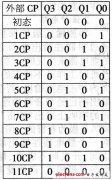
CR(RD)=(Q1Q0)百(Q1Q0 )拾(Q1)個 初態:0000
終態:233-1=232即:0010 0011 0010
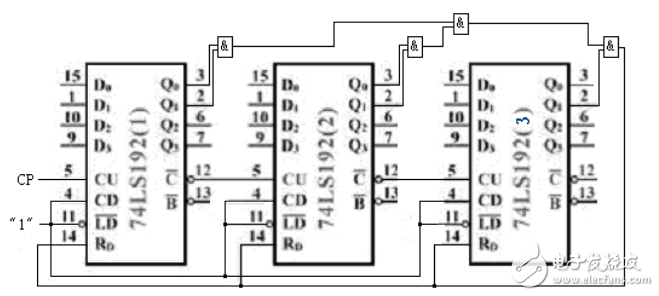
任意進制計數器設計方案三
LD=(Q1Q0)百(Q1Q0 )拾(Q2Q0)個 (或LD=CO)
初態:0000 (或1000-332=668)
終態:332-1=331即:0011 0011 0001 (或999)

任意進制計數器設計方案四:采用置數法來設計任意進制計數器1
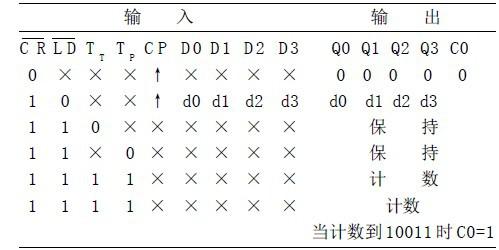
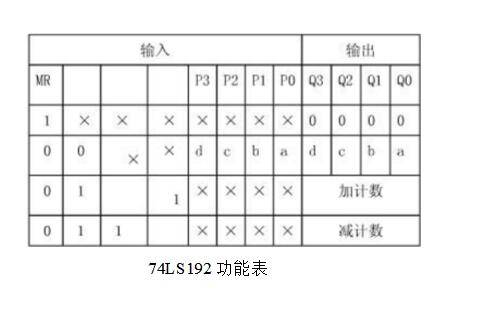
由于74LS192是具有異步清零、置數功能的十進制計數器,因此保留哪233種狀態,方法有多種。
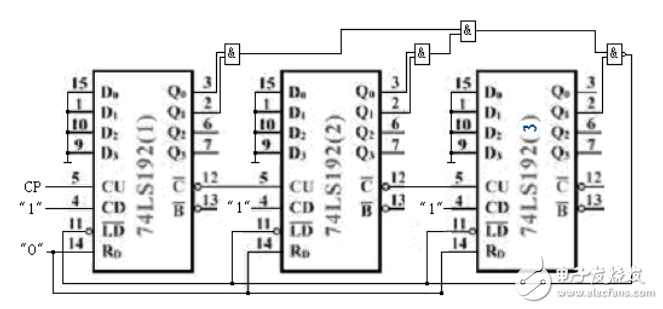
任意進制計數器設計方案五:采用置數法來設計任意進制計數器2
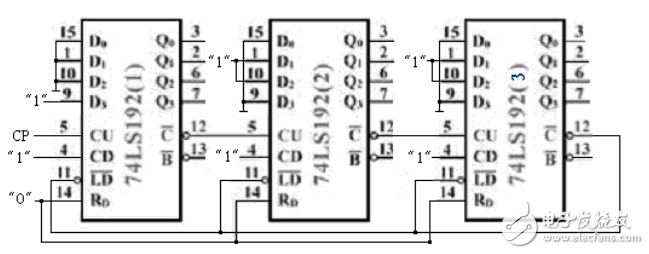
任意進制計數器設計方案六:任意進制計數器M小于N的情況
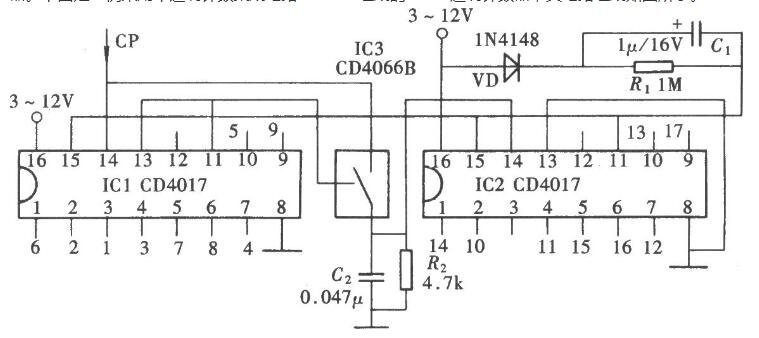
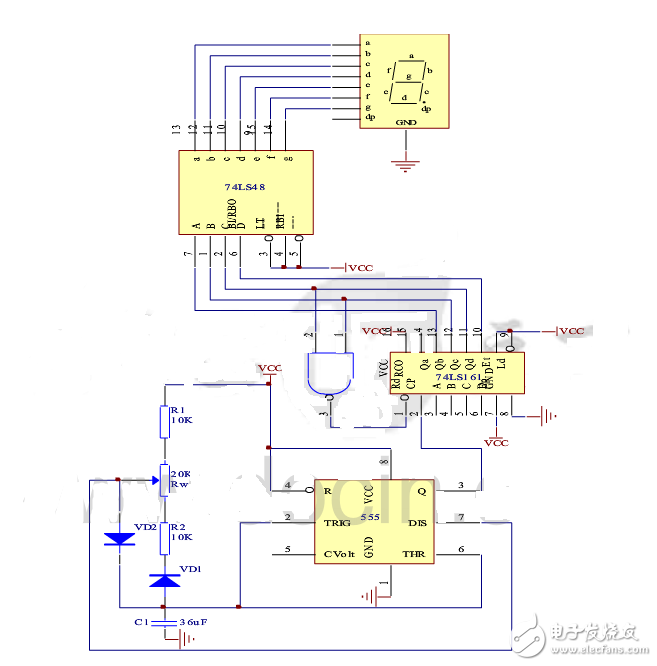
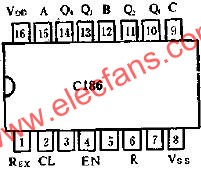
詳細電路設計方案:基于74LS192的任意進制計數器的設計
假定已有的是N進制計數器,需要得到的是M進制計數器。這時就有M小于N和M大于N兩種情況。
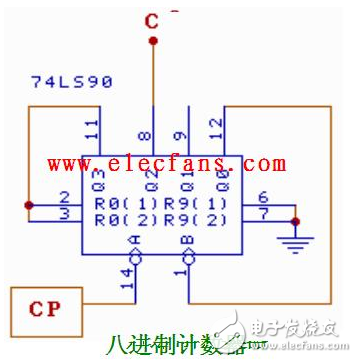
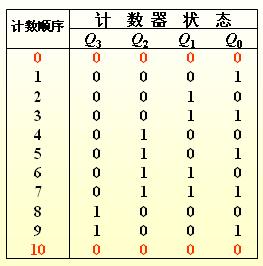
例題為用74LS192設計一個八進制計數器:
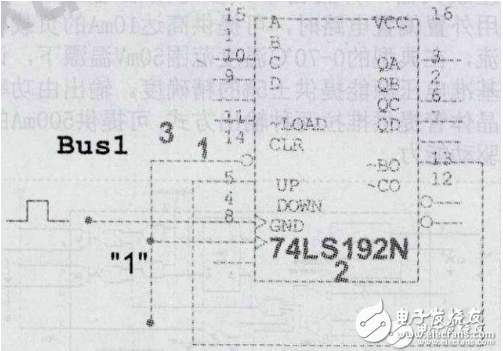
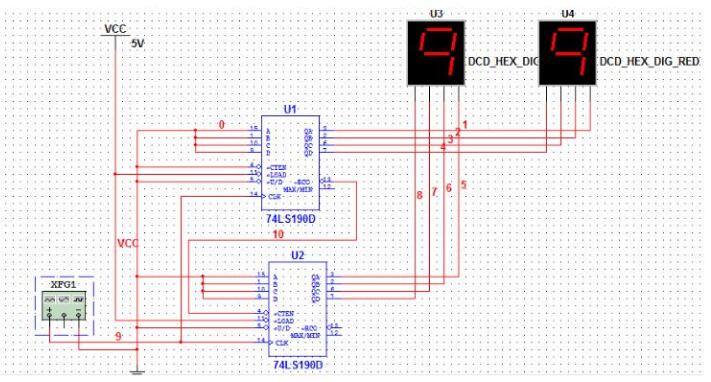
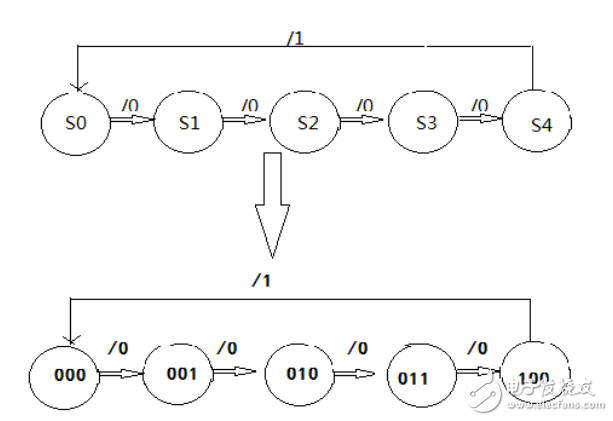
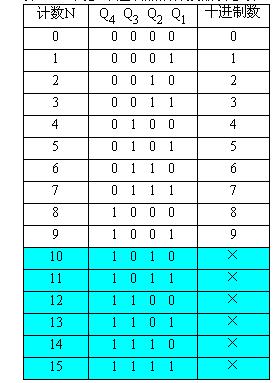
在N進制的計數器的計數順序中,使計數器的計數狀態跳過N-M的狀態,就可以得到M進制計數器,如例,74LS192是一個十進制計數器,如想得到八進制計數器,輸出狀態QAQBQCQD需要從0000―1110狀態,跳過0001及1001這兩個狀態。實現跳躍的方法有置零法和置數法這兩個方法。
置零法的方式為在輸入第M個計數脈沖CP后,利用計數器當前的輸出狀態SM進行譯碼產生清零信號加到清零端上,使計數器清零,即實現了M進制計數器。在計數器的有效循環中不包括狀態SM,所以狀態SM只在極短的時間內出現稱為過渡狀態。對于本例題來說,在輸入第八個時鐘脈沖后,當前的輸出狀態QAQBQCQD為0001,通過計數器輸出端QD的高電平信號給CLR清零端,將計數器置零,回到0000狀態。根據以上原理設計出的邏輯圖如下圖所示。
任意進制計數器設計方案七:任意進制計數器M大于N的情況
詳細電路設計方案:基于74LS192的任意進制計數器的設計
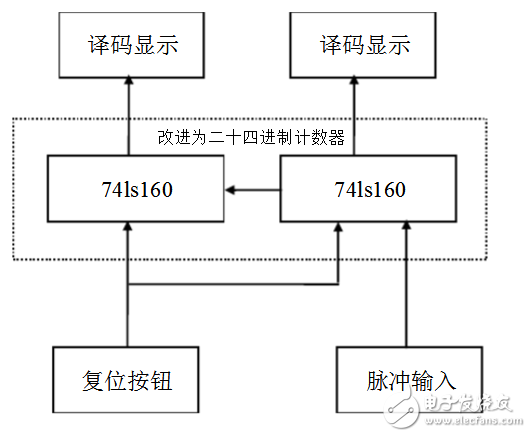
例題為用74LS192設計一個24進制的計數器。
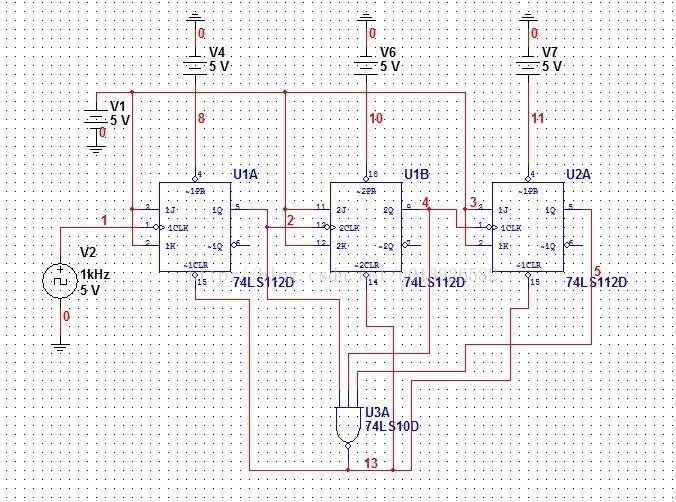
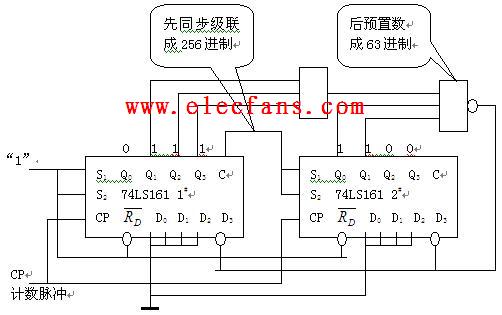
設計任意進制計數器M大于N的情況時必須要使用兩個以上的N進制集成電路進行組合來完成M進制計數器的設計,各個集成電路之間的連接方式可分為串行進位,并行進位,整體置零,整體置數等幾種方法。
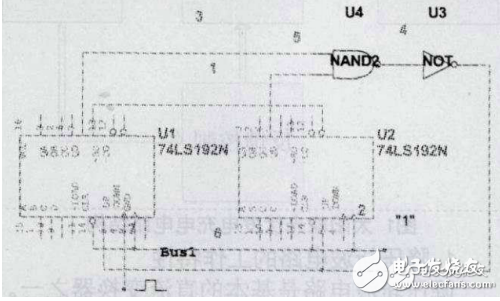
整體置零法就是將兩片N進制計數器級聯成大于M進制的計數器,然后在計數器輸出到達M狀態時,通過輸出狀態譯碼出清零信號同時送達兩個計數器的清零端,使兩個計數器同時清零,從而實現M進制,此方法類似于M小于N的置零法原理。對于74LS192來說,就是在兩片集成計數器輸出端QAQBQCQD到達0010(第一片低位)0100(第二片高位)狀態時,譯出清零信號同時送到兩個計數器的清零端。根據以上設計原理設計出下面的邏輯電路圖。
整體置數法的工作原理等同于M小于N的置數法原理,首先就是將兩片N進制計數器聯成大于M進制的計數器,然后選定所設計的M進制狀態,譯碼出置數端的有效工作信號,使N進制計數器置入置數輸入端規定的信號,跳過剩余的不用的狀態,從而實現M進制。用整體置數法使兩片74LS192完成24進制的設計方法可以參考M小于N的置數法以及以上的設計例題。
 電子發燒友App
電子發燒友App













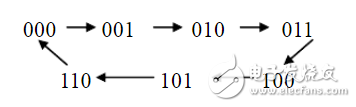















評論